Derive lens maker's formula for a thin biconvex lens.

Text Solution

Verified by Experts

Lens maker.s formula for biconvex lens
Sign Conventions
1. All the distances are measured from the optical centre of lens.
2. Distance measured in the direction of incident light is + ve.
3. Distance measured in the direction opposite to the direction of incident light is negative.
Assumptions
1. Object is a point object.
2. Lens is thin so that distances are measured fromthe poles of its surfaces.
3. The aperture of the lens is small.
4. Angles of incidence and refraction are small.
Let $C_{1}$ and $C_{2}$ be centres of curvature of two spherical surfaces ABC and ADC with optical centre C. Let $μ_{1}$ be the refractive index of the material of the lens and $μ_{1}$ that of the medium surrounding the lens where $μ_{2} > μ_{1}$ .
Consider a point object O lying on the principal axis of the lens.
Refraction at the surface ABC. A ray of light $O A L_{1}$ starting from O strikes the surface ABC at $A_{1}$ with $A_{1} C_{1}$ is a normal. On refraction it bends towards the normal and proceeds along $A_{1} I_{1}$ . Another ray OB starting from O and incident at B, passes through optical centre C. If the lens material were continuous, the two refracted rays would actually meet at $I_{1}$ . Thus $I_{1}$ , would be the real image of the point object.

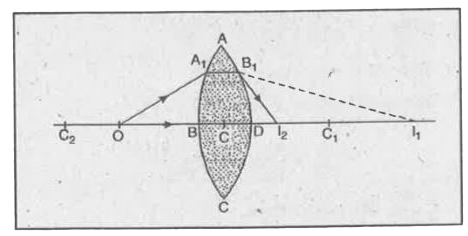
Applying spherical equation for surface ABC
$\frac{μ_{1}}{O B} + \frac{μ_{2}}{B I_{1}} = \frac{(μ_{2} - μ_{1})}{B C_{1}}$ ...(1)
This image $I_{1}$ , acts as an object for spherical interface ADC and thus final image $I_{2}$ is formed. $I_{2}$ is the effective position of the image corresponding to the lens ABCD as a whole.
$∴$ For surface ADC,
$- \frac{μ_{2}}{D I_{1}} + \frac{μ_{1}}{D I_{2}} = (\frac{μ_{2} - μ_{1}}{D C_{2}})$
But $D I_{1} \approx B I_{1}$ ( $∴$ lens is thin)
$- \frac{μ_{2}}{D I_{1}} + \frac{μ_{1}}{D I_{2}} = [\frac{μ_{2} - μ_{1}}{D C_{2}}]$ ...(2)
Adding (1) and (2), we get
$\frac{μ_{1}}{O B} + \frac{μ_{1}}{D I_{2}} = (μ_{2} - μ_{1}) (\frac{1}{B C_{1}} + \frac{1}{D C_{2}})$
If O is at infinity [i.e. $O B = \infty$ ] the image will be formed at principal focus, [i.e. $D I_{2} = f$ ]
$\frac{μ_{1}}{f} = (μ_{2} - μ_{1}) (\frac{1}{B C_{1}} + \frac{1}{D C_{2}})$ ...(3)
Applying new cartesian sign conventions, we get
$B C_{1} = R_{1}$ and $D C_{2} = - R_{2}$
So Eq. (3) becomes
$\frac{μ_{1}}{f} = (μ_{2} - μ_{1}) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
or $\frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
or $\frac{1}{f} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
where $μ = \frac{μ_{2}}{μ_{1}}$ , and is called relative refractive index of lens w.r.t. surroundings.

Lens maker's formula is applicable to
AThin lenses and paraxial rays which subtend very small angles with the principal axis
BThick lenses and paraxial rays which subtend very small angels with the principles axis
CThin lenses and for marginal rays
DThick lenses and for marginal rays
The lens maker's equation is given by
A $\frac{1}{f} = (\frac{μ_{1}}{μ_{2}} - 1) (\frac{1}{R_{1}} + \frac{1}{R_{2}})$
B $\frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) (\frac{1}{R_{1}} + \frac{1}{R_{2}})$
C $\frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
D $\frac{1}{f} = (\frac{μ_{1}}{μ_{2}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$