Determine the potential at a point 0.50 m (i) from a+20μC potential charge (ii) from a−20μC point charge.
To determine the electric potential at a point 0.50 m from a charge of +20 µC and then from a charge of -20 µC, we can use the formula for electric potential due to a point charge:
V=14πϵ0QR
where:
- V is the electric potential,
- Q is the charge,
- R is the distance from the charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- 14πϵ0 is approximately 9×109N m2/C2.
Step 1: Calculate the potential due to +20 µC charge
1. Identify the charge and distance:
- Charge Q=+20μC=20×10−6C
- Distance R=0.5m
2. Substitute the values into the potential formula:
V=14πϵ0QR=9×109×20×10−60.5
3. Calculate the potential:
V=9×109×20×10−60.5=9×109×40×10−6=3.6×105V
Step 2: Calculate the potential due to -20 µC charge
1. Identify the charge and distance:
- Charge Q=−20μC=−20×10−6C
- Distance R=0.5m
2. Substitute the values into the potential formula:
V=14πϵ0QR=9×109×−20×10−60.5
3. Calculate the potential:
V=9×109×−20×10−60.5=9×109×−40×10−6=−3.6×105V
Final Results:
- The potential at a point 0.50 m from the +20 µC charge is 3.6×105V.
- The potential at a point 0.50 m from the -20 µC charge is −3.6×105V.
- V is the electric potential,
- Q is the charge,
- R is the distance from the charge,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- 14πϵ0 is approximately 9×109N m2/C2.
- Charge Q=+20μC=20×10−6C
- Distance R=0.5m
V=14πϵ0QR=9×109×20×10−60.5
V=9×109×20×10−60.5=9×109×40×10−6=3.6×105V
- Charge Q=−20μC=−20×10−6C
- Distance R=0.5m
V=14πϵ0QR=9×109×−20×10−60.5
V=9×109×−20×10−60.5=9×109×−40×10−6=−3.6×105V
- The potential at a point 0.50 m from the +20 µC charge is 3.6×105V.
- The potential at a point 0.50 m from the -20 µC charge is −3.6×105V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The potential at a point 0.1 m from an isolated point charge is + 100 volt. The nature of the point charge is
View SolutionTwo tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View Solution
Knowledge Check
In the question number 18, the potential at a point 20 cm from the mid-point of the line joining the two charges in a plance normal to the line and passing through the mid-point is
A1.4×105VB4.2×103VC2.9×104VD3.7×105VThe work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
Find out electric field intensity at point A (0, 1m, 2m) due to a point charge −20μC situated at point B(√2m,0,1m).
View SolutionThe potential of a point B (-20m, 30m) taking the potential of a point A (30m, -20m) to be zero in an electric field →E=10xˆi−20ˆjNC−1 is
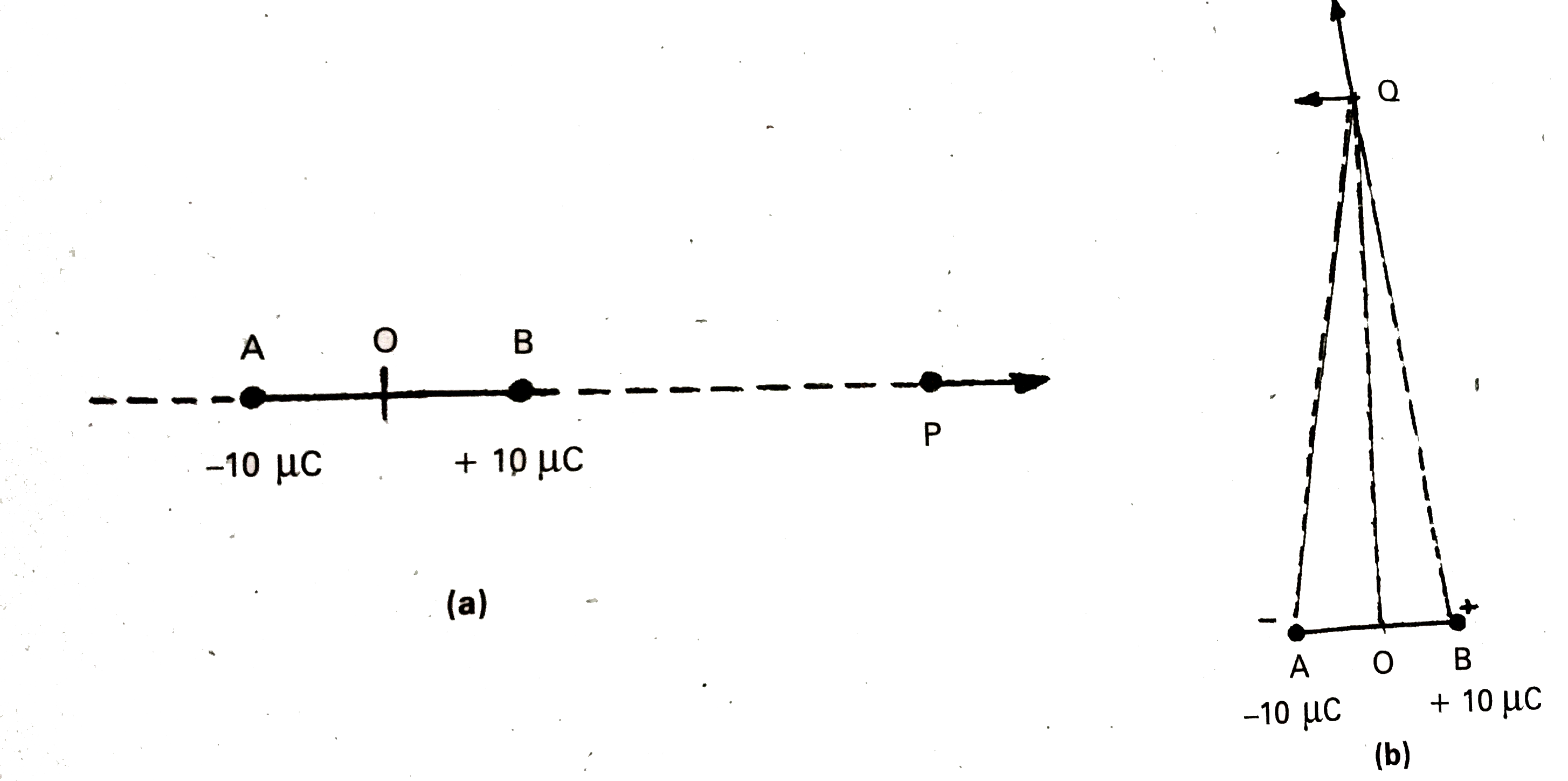
View SolutionTwo charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
View SolutionA point charge 20μC is shifted from infinity to a point P in an electric field with zero acceleration. If the potential of that point is 1000 volt, then
(i) Find out work done by electric field ?
(iii) If the kinetic energy of charge particle is found to increase by 10 mJ when it is brought from infinity to point P, then what is the total work done by external agent ?
(iv) What is the work done by electric field in the part (iii)
(v) If a point charge 30μC is released at rest at point P, then find out its kinetic energy at a large distance ?
View SolutionElectrostatic force experienced by −3μC charge placed at point 'P' due to a system 'S' of fixed point charges as shown in figure is →F=(21ˆi+9ˆj)μN.
(i) Find out electric field intensity at point P due to S.
(ii) If now, 2μC charge is placed and −3μC is removed at point P then force experienced by it will be.
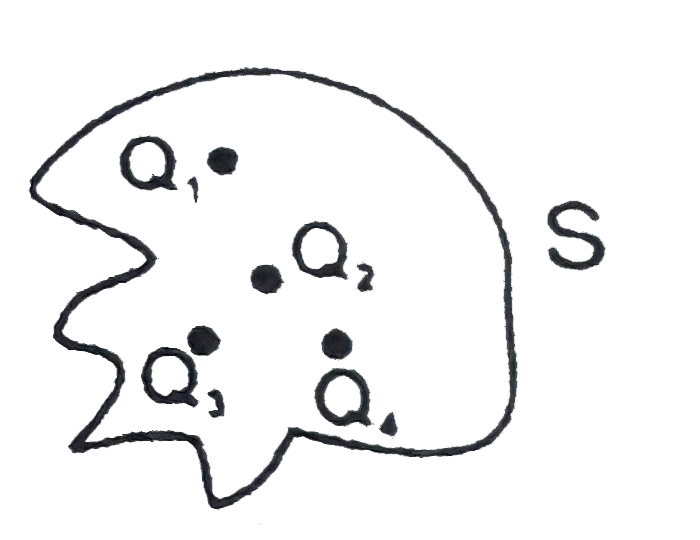
View SolutionFind the work done in taking a charge 100μC from C & D.
View Solution

