Due to flow of current I through a square shaped conducting loop, magnetic field generated at its centre is B. the magnetic field generated at the centre of a circular conducting loop having the same perimeter as that of the square and for the flow of the same current is B'. determine the ratio of B to B'.Solution in Bengali
Magnetic field at the centre of the circular loop of radius r,
B'=μ0I2r, circumference of the circle 2πr
So, the perimeter of the given, square loop 2π=r and hence the lengh of the each side,
a=2πr4=πr2
Magnetic field at the centre of the square loop,
B=μ04π⋅8√2Ia
=μ04π⋅8√2Iπr2=4√2μ0Iπ2r=8√2π2⋅μ0I2r=8√2π2B'
So, BB'=8√2π2
Topper's Solved these Questions
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT
25 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - NCERT EXAMPLAR QUESTIONS WITH ANSWER HINT (MCQ-1)
2 Videos
- ELECTROMAGNETISM BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETISM EXERCISE - SECTION RELATED QUESTIONS
64 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
- ELEMENTARY PHENOMENA OF ELECTROSTATICS BOOK - CHHAYA PUBLICATIONCHAPTER - ELEMENTARY PHENOMENA OF ELECTROSTATICS EXERCISE - EXAMINATION ARCHIVE
2 Videos
Similar Questions
Two moving coils meters M1andM2 have the following particulars :
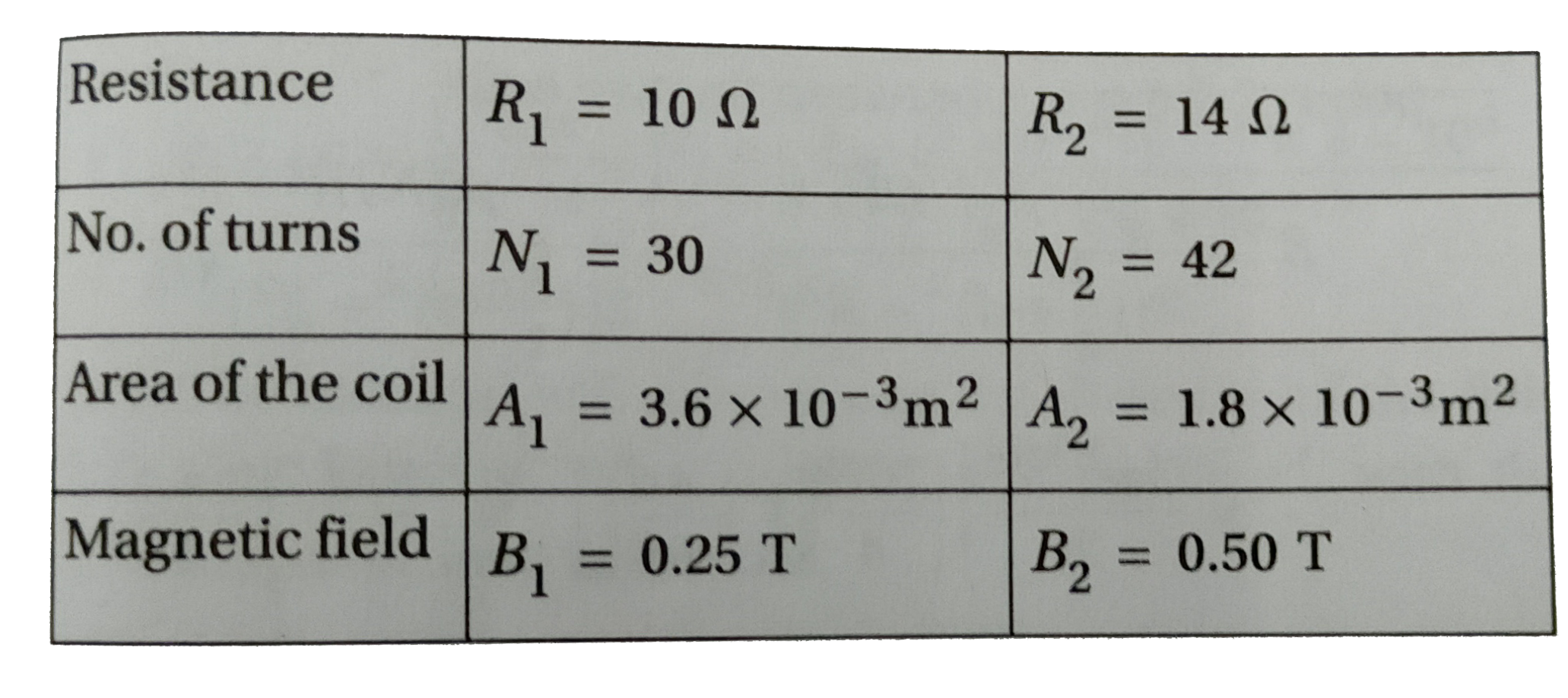
(The spring constancs are identical for the two meters ).
View SolutionTwo charged particles traverses indentical helical paths in a completely opposite sense in a uniform magnetic field, →B=B0ˆK.
View SolutionWhat are the fundamental properties of a magnet ?
View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
View SolutionDefine surface density of electric charge
View SolutionA square loop of side a carris a current I . The magnetic field at the centre of the loop is
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionA square frame of side l carries a current produces a field B at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is B' , the ratio of B//B' is
View SolutionA steady current flows in a long wire. It is bent into a circular loop of one turn and the magnetic field at the center of the coil is B. If the same wire is bent into a circular loop of n turns, the magnetic field at the center of the coil is
View SolutionA square loop of a conducting material of side l and resistance r is dragged through a uniform magnetic field B with uniform velocity v keeping the plane of the loop perpendicular to the direction of the field. What is the current flowing through the loop?
View SolutionIf a square frame of side L is made from a uniform wire and current I is flowing through it and its magnetic field intensity at the centre is B_(1) . When the same current is passed through the circular loop whose circumference is same as that of the square, the magnetic field at the centre is B_(2) . What will be B_(1)//B_(2) ?
View Solutionएक वृत्ताकार लूप का पृष्ठ क्षेत्रफल A तथा इसमें प्रवाहित धारा I है चुम्बकीय क्षेत्र की तीव्रता B, लूप के तल के लम्बवत है। चुम्बकीय क्षेत्र के कारण लूप में लगने वाला बल-आघूर्ण है -
View SolutionA square frame of side l carries a current produces a field B at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is B' , the ratio of B//B' is
View SolutionBy flowing an I current in a square of 1 m side, a B magnetic field is generated at its center. When the current flows here in a circular coil with circumference equal to the square perimeter, then the B magnetic field is generated at its center. The ratio is B / B.
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View Solution
