Find the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
Let M and R be the mass and radius of the half - disc mass per unit area unit aera of the half - disc
m=M12πR2=2MπR2
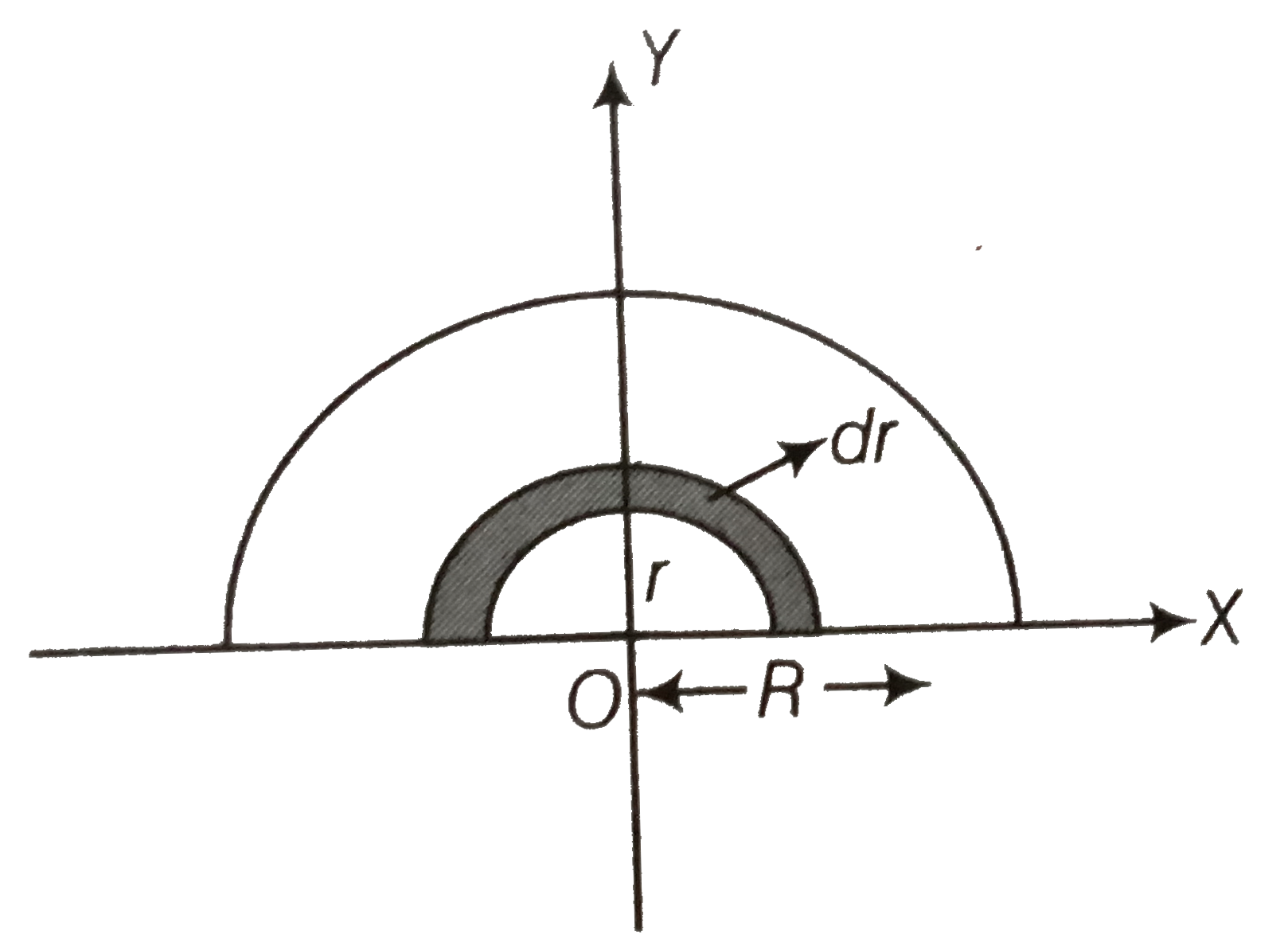
(a) the half -disc can be supposed to be consists of a large number of semicircular rings of mass dm and thickness dr and ranging from r=0 to r=R
Surface area of semicircular ring of radius r and of thickness dr=122πr×dr=πrdr
∴Mass of this elemetary ring dm=πrdr×2MπR2
dm=2MR2rdr
If (x,y) are coordinates of centre of mass of this element,
then, (x,y)=(0,2rπ)
therefore , x=0andy=2rπ
Let xcM and yCM be the coordinates of the centre of the centre of the semicircular disc.
then xCM=1M∫R0xdm=1M∫R0dm=0
yCM=1M∫R0ydm=1M∫R02lπ×(2MR2rdr)
=4πR2∫R0r2dr=4πR2[r33]R0
=4πR2×(R33−0)=4R3π
∴ Centre of mass of the semicicular disc =(9,4R3π)
( b) Centre of mass a unifrom quarter disc,
Mass per unit area of the quarter disc =MπR24=4M3ΠR3
Using symmetry
for a half along y - axis centre of mass will be at x=4R3π
For a half - disc along x-axis centre of mass will be at x=$R3π
Hence , for the quarter disc centre of mass =(4R3π,3R3π)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - OSCILLATIONSEXERCISE - All Questions
36 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
Knowledge Check
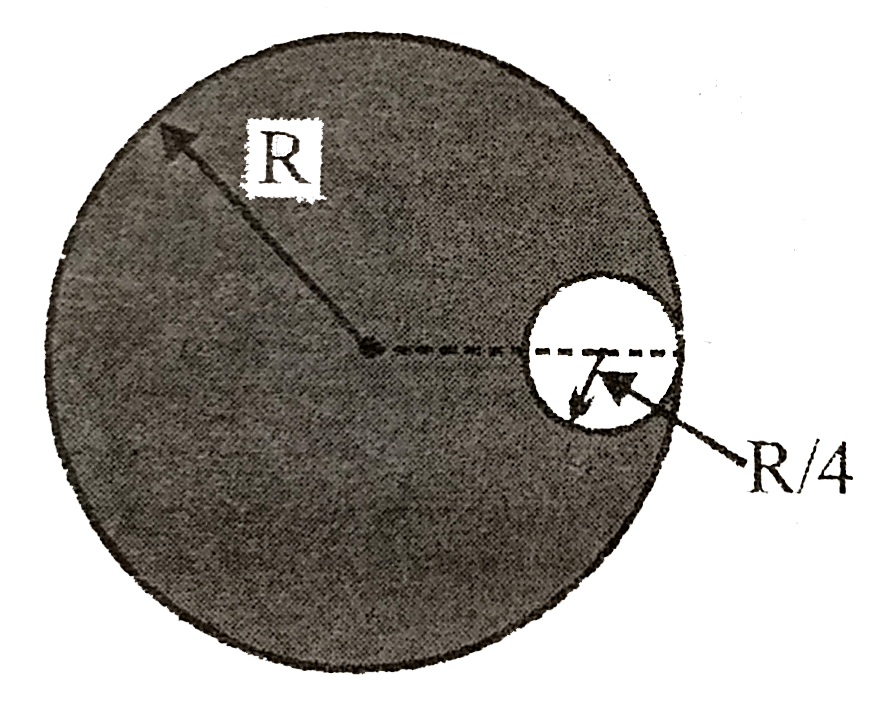
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
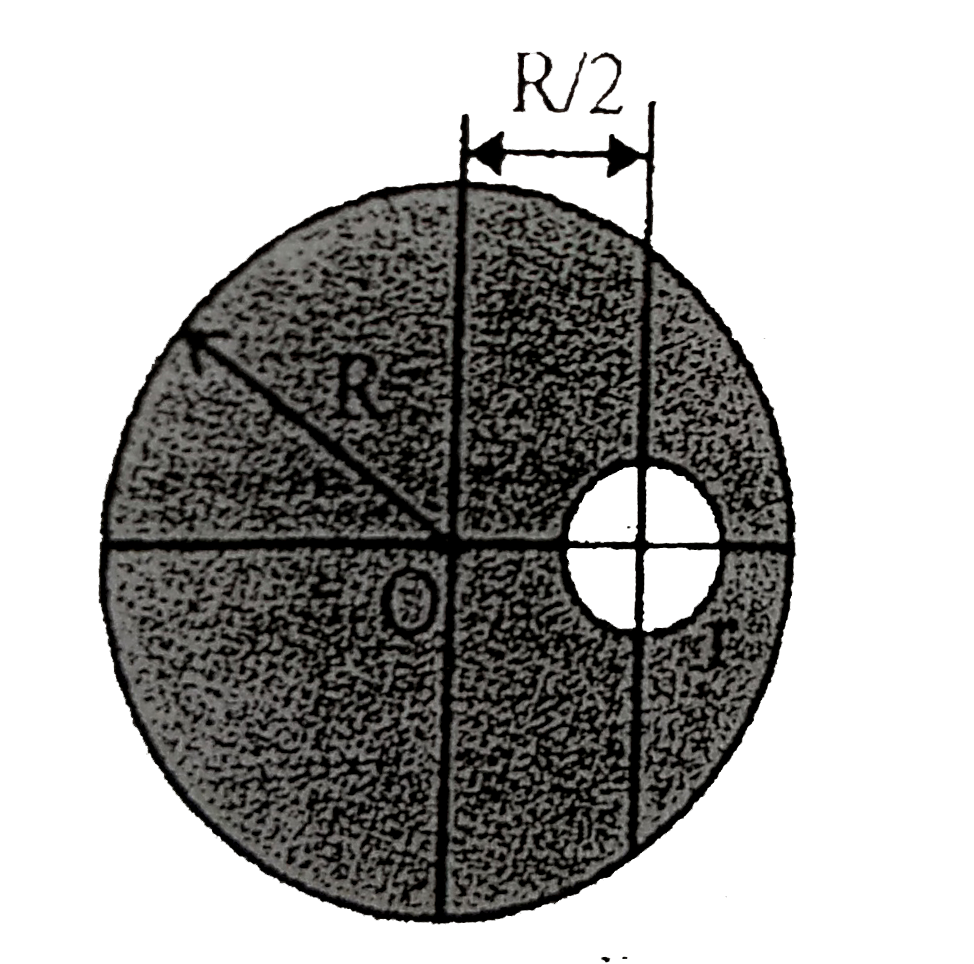
Find the centre of mass of the shaded portion of a disc.
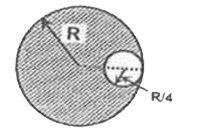
View SolutionFind the centre of mass of the shaded portion of a disc.

View SolutionFind the centre of mass of a uniform disc of radius a from which a circualr section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionFind the centre of mass of the disc shown in figure. . A square is removed from the disc as shown
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View Solution