Find the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0A at its centre of curvature .
To find the magnetic field B due to a semicircular wire of radius 10.0cm carrying a current of 5.0A at its center of curvature, we can follow these steps:
Step 1: Understand the Problem
We need to calculate the magnetic field at the center of a semicircular wire carrying a current. The radius of the semicircle is given as r=10.0cm and the current I=5.0A.
Step 2: Convert Units
Convert the radius from centimeters to meters for consistency in SI units:
r=10.0cm=10.0×10−2m=0.1m
Step 3: Use the Formula for Magnetic Field
The formula for the magnetic field at the center of a semicircular wire carrying current is given by:
B=μ0I4R
where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes,
- R is the radius of the semicircle in meters.
Step 4: Substitute the Values
Substituting the known values into the formula:
B=4π×10−7T m/A×5.0A4×0.1m
Step 5: Simplify the Expression
The 4 in the numerator and denominator cancels out:
B=π×10−7×5.00.1
B=5π×10−70.1
B=5π×10−6T
Step 6: Calculate the Value
Using π≈3.14:
B≈5×3.14×10−6T
B≈15.7×10−6T
B≈1.57×10−5T
Final Answer
The magnetic field B at the center of the semicircular wire is approximately:
B≈1.57×10−5T
---
We need to calculate the magnetic field at the center of a semicircular wire carrying a current. The radius of the semicircle is given as r=10.0cm and the current I=5.0A.
Convert the radius from centimeters to meters for consistency in SI units:
r=10.0cm=10.0×10−2m=0.1m
The formula for the magnetic field at the center of a semicircular wire carrying current is given by:
B=μ0I4R
where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes,
- R is the radius of the semicircle in meters.
Substituting the known values into the formula:
B=4π×10−7T m/A×5.0A4×0.1m
The 4 in the numerator and denominator cancels out:
B=π×10−7×5.00.1
B=5π×10−70.1
B=5π×10−6T
Using π≈3.14:
B≈5×3.14×10−6T
B≈15.7×10−6T
B≈1.57×10−5T
The magnetic field B at the center of the semicircular wire is approximately:
B≈1.57×10−5T
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
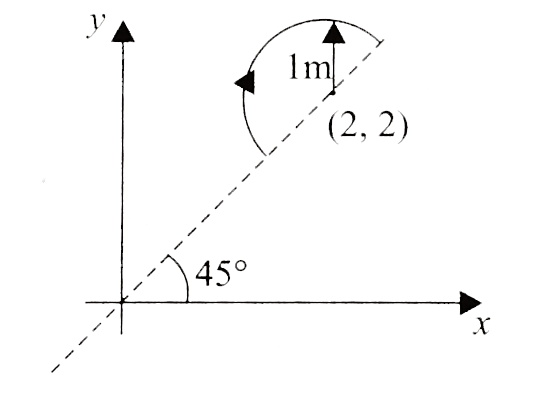
View SolutionA uniform magnetic field →B=3ˆi+4ˆj+ˆk exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
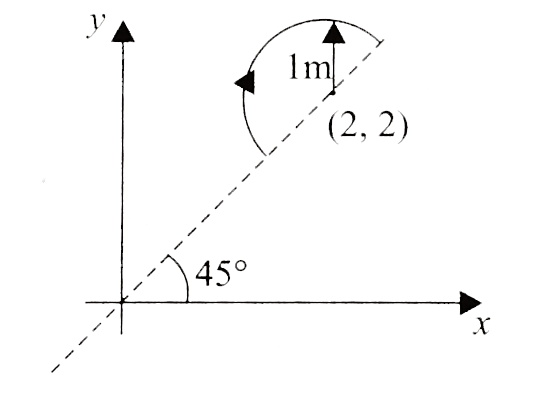
View Solution
Knowledge Check
The magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is
A18GB19.7GC15.7GD17.7G
A long straight wire is bent as shown below. Find the resultant magnetic field B at the centre C of the circular path of radius 2 cm if a current I of 5A is passed through the wire.

View SolutionFind the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionMagnetic field intensity at the centre of coil of 50 turns, radius 0.5m and carrying a current of 2A is
View SolutionCalculate magnetic flux density of the magnetic field at the centre of a circular coil of 50 turns, having radius of 0.5 m and carrying a current of 5A.
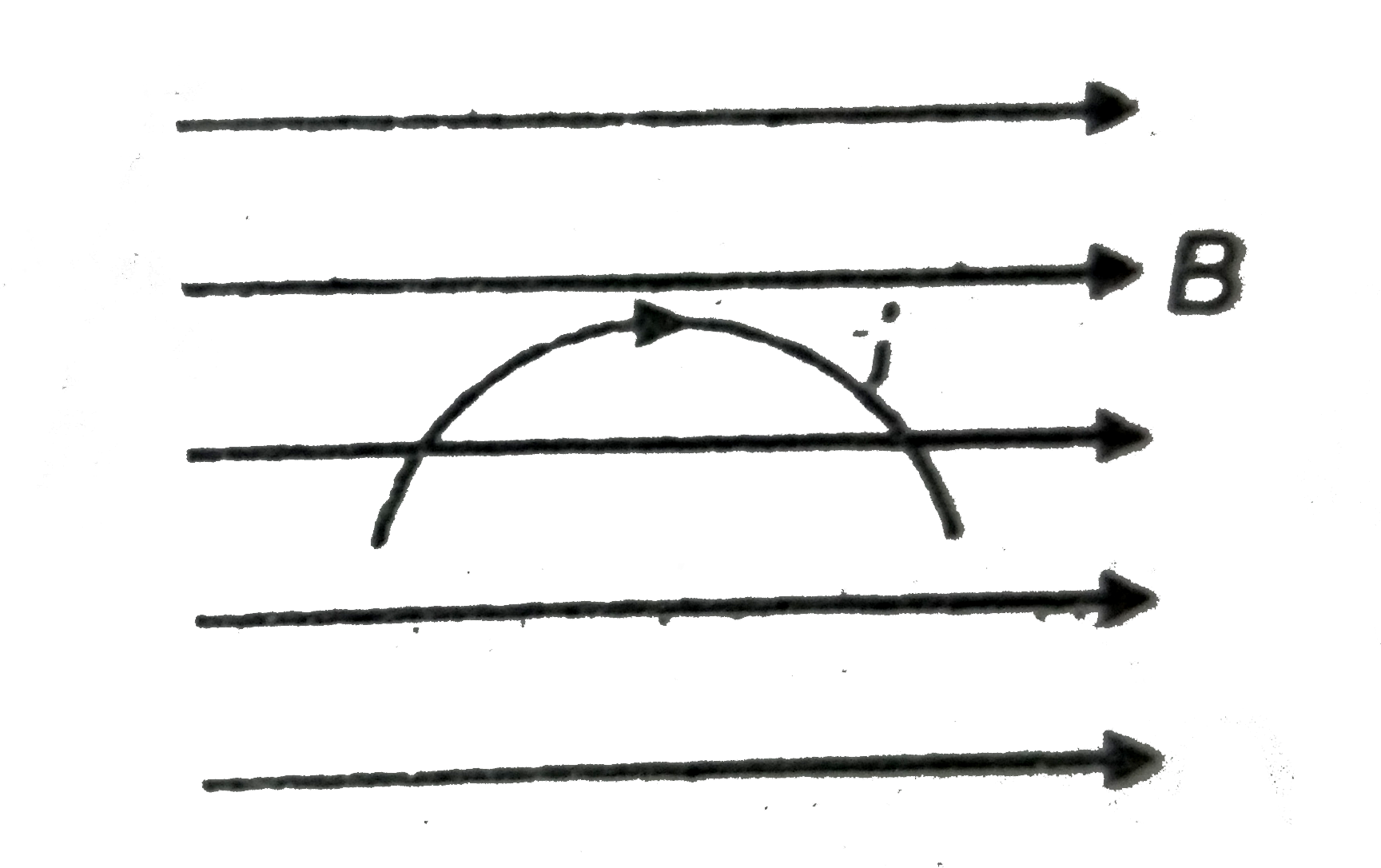
View SolutionWhat is the force experienced by a semicircular wire of radius R when it is carrying a current l and is placed in a uniform magnetic field of induction B as shown in figure. ?
View SolutionThe magnetic field due to a current carrying circular loop of radius 3 cm at a point on the axis at a distance of 4cm from the centre is 54μT. What will be its vlue at the centre of loop?
View SolutionThe magnetic field due to current carrying circular coil loop of radius 6 cm at a point on axis at a distance of 8 cm from the centre is 54μT . What is the value at the centre of loop ?
View Solution