Find the period of a vertical spring - block system by both methods.
The correct Answer is:A
To find the period of a vertical spring-block system using both the force method and the energy method, we can follow these steps:
Step 1: Understanding the System
We have a vertical spring with spring constant k and a block of mass m attached to it. When the block is at rest, it will stretch the spring until it reaches an equilibrium position where the gravitational force on the block equals the spring force.
Step 2: Force Method
1. Equilibrium Condition: At equilibrium, the force due to gravity is balanced by the spring force.
mg=kx0
where x0 is the extension of the spring at equilibrium.
2. Displacement from Equilibrium: When the block is displaced further by a distance x from the equilibrium position, the net force acting on the block is given by:
F=−k(x+x0)+mg
Since mg=kx0, we can simplify this to:
F=−kx
3. Simple Harmonic Motion (SHM): The equation F=−kx indicates that the motion is simple harmonic motion. The time period T of SHM is given by:
T=2π√mk
Step 3: Energy Method
1. Total Energy at Mean Position: At the mean position (equilibrium), the total mechanical energy is the sum of kinetic and potential energy. When the block is displaced to a position C:
- Kinetic Energy (KE) at position C:
KE=12mv2
- Potential Energy (PE) due to spring at position C:
PE=12k(x+x0)2−mgx
2. Conservation of Energy: The total energy remains constant. Therefore, we can set up the equation:
12mv2+(12k(x+x0)2−mgx)=constant
3. Differentiating Energy: Since the total energy is constant, we can differentiate with respect to time to find relationships between the forces:
dEdt=0
This leads to:
12m(2v)dvdt+k(x+x0)dxdt−mgdxdt=0
4. Substituting Known Values: Using F=ma and kx0=mg, we can simplify and arrive at the same conclusion:
F=−kx
This again indicates SHM.
5. Final Result for Time Period: The time period T remains:
T=2π√mk
Conclusion
In both methods, we arrive at the same expression for the time period of the vertical spring-block system:
T=2π√mk
We have a vertical spring with spring constant k and a block of mass m attached to it. When the block is at rest, it will stretch the spring until it reaches an equilibrium position where the gravitational force on the block equals the spring force.
1. Equilibrium Condition: At equilibrium, the force due to gravity is balanced by the spring force.
mg=kx0
where x0 is the extension of the spring at equilibrium.
F=−k(x+x0)+mg
Since mg=kx0, we can simplify this to:
F=−kx
T=2π√mk
1. Total Energy at Mean Position: At the mean position (equilibrium), the total mechanical energy is the sum of kinetic and potential energy. When the block is displaced to a position C:
- Kinetic Energy (KE) at position C:
KE=12mv2
- Potential Energy (PE) due to spring at position C:
PE=12k(x+x0)2−mgx
12mv2+(12k(x+x0)2−mgx)=constant
dEdt=0
This leads to:
12m(2v)dvdt+k(x+x0)dxdt−mgdxdt=0
F=−kx
This again indicates SHM.
T=2π√mk
In both methods, we arrive at the same expression for the time period of the vertical spring-block system:
T=2π√mk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 1
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 2
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Time period of a given spring-mass system is

View SolutionIn spring-block system match the following

View SolutionIn a spring-block system, match the following:
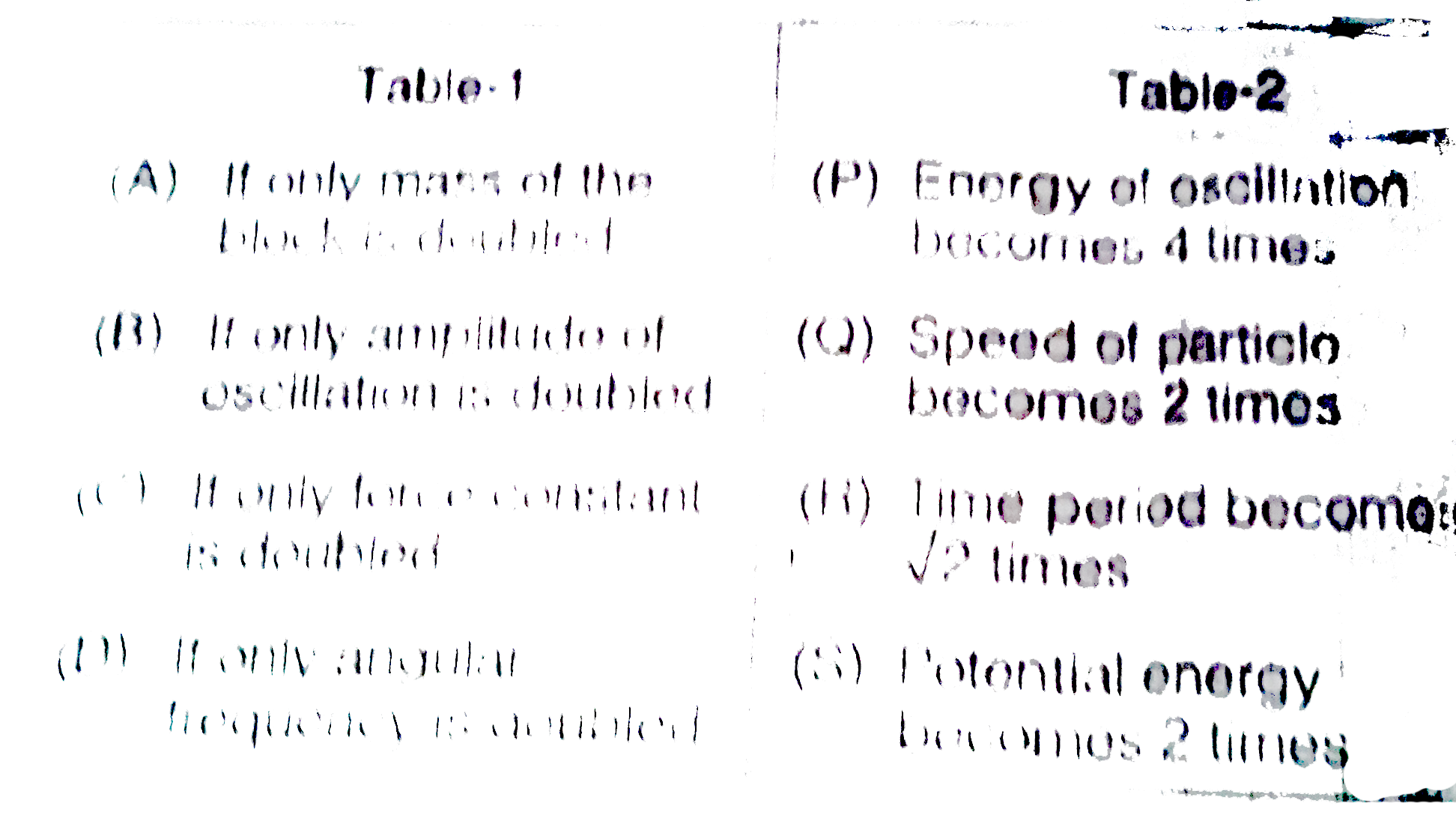
View SolutionSpring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

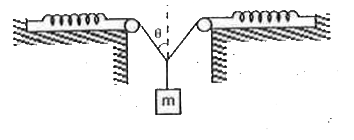
View SolutionConsider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
View SolutionA: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.
View SolutionA block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
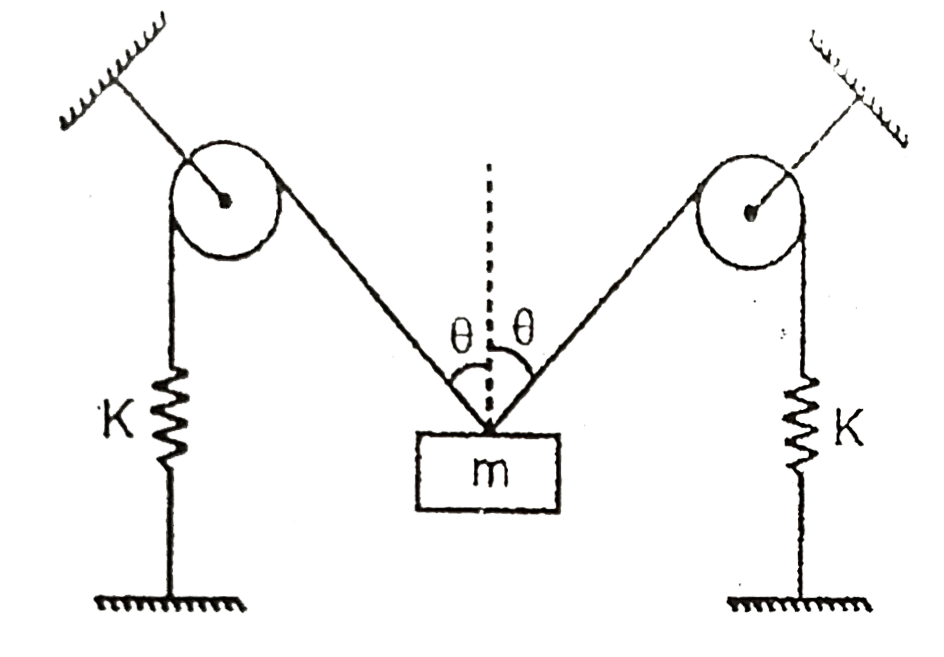
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
View Solution
