Four cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
2E4r+R
3E4r+R
3E3r+R
2E3r+R
The correct Answer is:A
To solve the problem of finding the current in the external circuit when four cells are connected in series, with one cell connected in reverse, we can follow these steps:
1. Identify the Configuration:
- We have four cells, each with an emf (E) and internal resistance (r), connected in series.
- One of the cells is connected in reverse.
2. Determine the Total EMF:
- The total emf (E_total) of the series circuit can be calculated considering the orientation of the cells.
- Three cells are connected in the same direction, contributing positively to the total emf, while one cell is connected in the opposite direction, contributing negatively.
- Therefore, the total emf is:
Etotal=3E−E=2E
3. Calculate the Total Internal Resistance:
- Since all four cells have the same internal resistance (r) and are in series, the total internal resistance (R_internal) is:
Rinternal=r+r+r+r=4r
4. Set Up the Circuit Equation:
- According to Kirchhoff's loop rule, the sum of the potential differences in the circuit must equal zero.
- The equation can be set up as follows:
Etotal−I⋅Rinternal−I⋅R=0
- Substituting the values we have:
2E−I⋅(4r+R)=0
5. Solve for Current (I):
- Rearranging the equation gives us:
I⋅(4r+R)=2E
- Therefore, the current (I) in the circuit is:
I=2E4r+R
Final Answer:
The current in the external circuit is:
I=2E4r+R
- We have four cells, each with an emf (E) and internal resistance (r), connected in series.
- One of the cells is connected in reverse.
- The total emf (E_total) of the series circuit can be calculated considering the orientation of the cells.
- Three cells are connected in the same direction, contributing positively to the total emf, while one cell is connected in the opposite direction, contributing negatively.
- Therefore, the total emf is:
Etotal=3E−E=2E
- Since all four cells have the same internal resistance (r) and are in series, the total internal resistance (R_internal) is:
Rinternal=r+r+r+r=4r
- According to Kirchhoff's loop rule, the sum of the potential differences in the circuit must equal zero.
- The equation can be set up as follows:
Etotal−I⋅Rinternal−I⋅R=0
- Substituting the values we have:
2E−I⋅(4r+R)=0
- Rearranging the equation gives us:
I⋅(4r+R)=2E
- Therefore, the current (I) in the circuit is:
I=2E4r+R
The current in the external circuit is:
I=2E4r+R
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns4videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View Solution
Knowledge Check
- Question 1 - Select One
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
n identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA student is asked to connected four cells of e.m.f of 1 V and internal resistance 0.5 ohm in series with a external resistance of 1 ohm. But one cell is wrongly connected by him with its terminal reversed, the current in the circuit is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
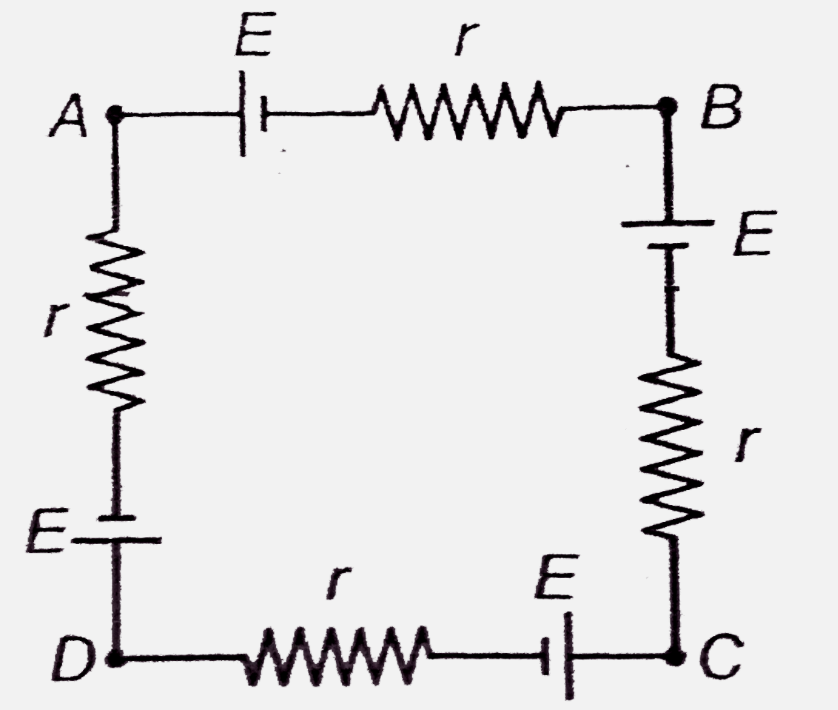 View Solution
View SolutionA cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, verses 'R.
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solution

