Four equal charges of value +Q are placed at any four vertices of a regular hexagon of side a. By suitably choosing the vertices, what can be the maximum possible magnitude of electric field at the centre of the hexagon?
(A) Q4π∈0a2
(B) √2Q4π∈0a2
(C) √3Q4π∈0a2
(D) 2Q4π∈0a2Solution in Bengali
Q4π∈0a2
√2Q4π∈0a2
√3Q4π∈0a2
2Q4π∈0a2
If the four +Q charges are placed at four adjacent vertices, then the net electric field at point O will be maximum and the electric field (E1) due to each charge will be equal in magnitude.
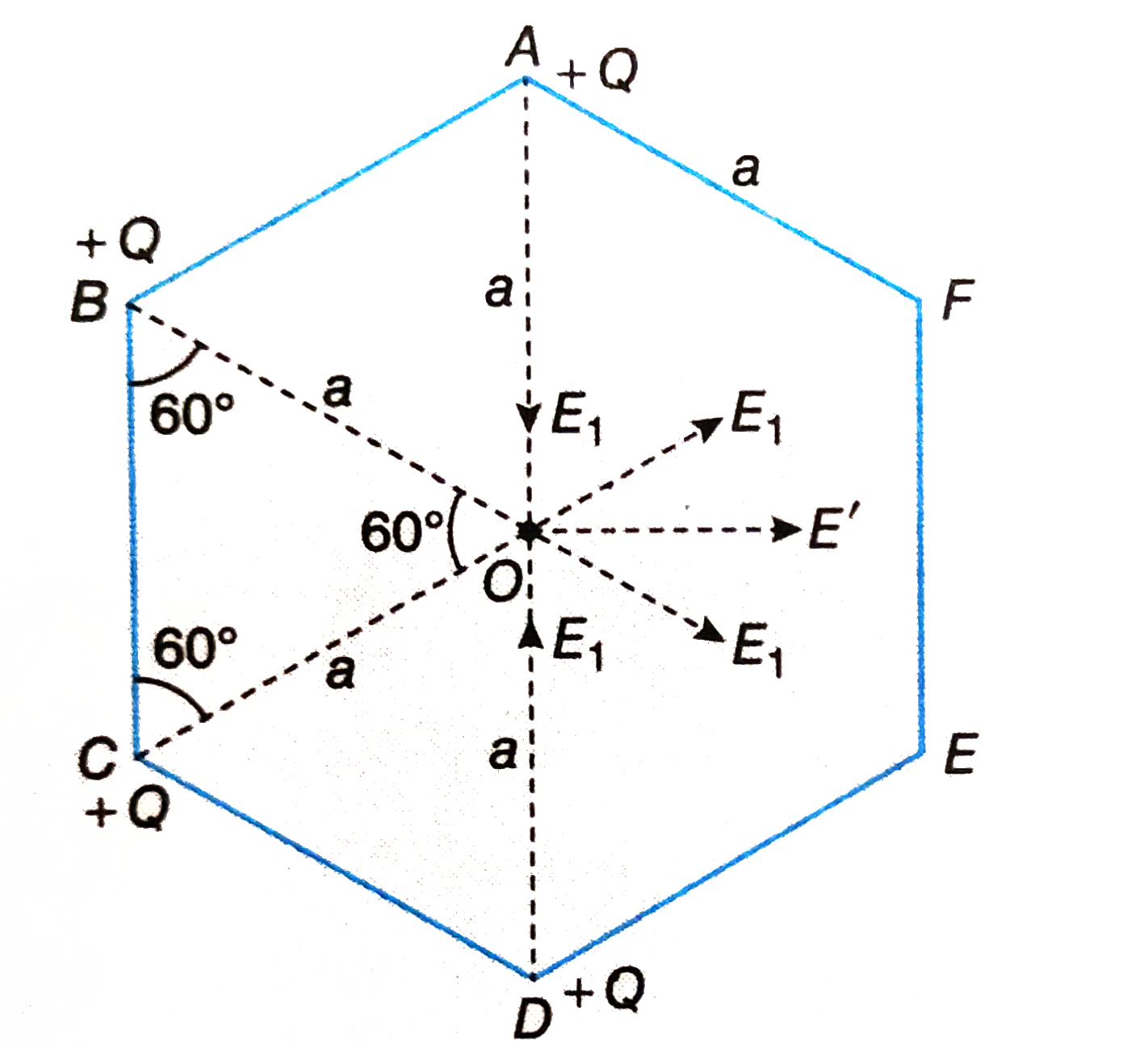
Since, ABCDEF, is a regular hexagon,
So, AO=BO=CO=DO=a
The net electric field at point O due to +Q charges placed at points A and D is zero. Hence the net electric field at point O due to +Q charges placed at points B and C is the maximum values of the electric field.
Now, E1=Q4π∈0a2
∴E'=√E21+E21+2E1E1cos60∘=√3Q4π∈0a2
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( JEE MAIN )
3 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( AIPMT)
1 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE (WBCHSE)
13 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
A long cylindrical shell carries positive surface charge σ in the upper half and negative surface charge −σ in the lower half. The electric field lines around the cylinder will look like figure given in (figures are schematic and not drawn to scale)
View SolutionThe eletric field in a certina region is acting radially outward and is given by E = Ar. A charge contained in 'a' centred at the origin of the field will be givne by
View SolutionFour point charges +q,+q,+q and −q are placed at the four comers of a square, length of each side of which is a.
Find the magnitude of the intensity of the electric field at the centre of the square.
View SolutionA light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate
the resistance of the bulb ,
View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.
View SolutionFive point charge ( +q each) are placed at the five vertices of a regular hexagon of side 2a .what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionFive point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
View SolutionFind the magnitude of the electric field at the point P in the configuration shown in figure- 1.219 (a), (b) and (c ) for d>>a take 2qa=P.
[(a)q4π∈0d2,(b)2q2π∈0d3,(c)q4π∈0d2√1+4a2d2]

View SolutionFind the potential energy of a charge q0 placed at the centre of regular hexagon of side a, if charge q is placed at each vertex of regular hexagon ?
View Solutionसिद्ध कीजिए की किसी गोलीय चालक की धारिता उसकी त्रिज्या की 4π∈0 गुनी होती है |
View SolutionThe elctric potential at any point due to a point charge is v=14π∈0qr.In analogy with this ,What will be magnetic potential at any point due to a magnetic charge?
View SolutionThe electric intensity at any point due to point charge is E=14π∈0×qr2.In analogy with this,What will be magnetic iduction at a point due to a magnetic charge?
View SolutionFour identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionFive point charges, each of value +q coulomb, are placed on five vertices of a regular hexagon of side L meters. The magnitude of the force on the point charge of value -q coulomb, placed at the centre of the hexagon is…………….
View Solution
