If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
1:2:3
1:13:15
1:3:5
5:3:1
The correct Answer is:B
To solve the problem of finding the ratio of wavelengths λ1,λ2, and λ3 for a closed organ pipe, we can follow these steps:
Step 1: Understand the Resonance Conditions
For a closed organ pipe, the fundamental frequency (first harmonic) has one node at the closed end and one antinode at the open end. The wavelengths for the fundamental and overtones can be described as follows:
- Fundamental (1st harmonic): λ1=4L
- First overtone (2nd harmonic): λ2=4L3
- Second overtone (3rd harmonic): λ3=4L5
Step 2: Set Up the Equations
From the resonance conditions:
1. For the fundamental mode:
L=λ14⇒λ1=4L
2. For the first overtone:
L=3λ24⇒λ2=4L3
3. For the second overtone:
L=5λ34⇒λ3=4L5
Step 3: Find the Ratios
Now we can find the ratios of the wavelengths:
- From the equations derived:
- λ1=4L
- λ2=4L3
- λ3=4L5
We can express the ratios λ1:λ2:λ3 as follows:
λ1λ2=4L4L3=3
λ2λ3=4L34L5=53
Step 4: Combine the Ratios
We can combine these ratios:
- Let λ1:λ2=3:1
- Let λ2:λ3=5:3
Now, we can express all three wavelengths in terms of a common variable:
- Let λ2=1k
- Then λ1=3k
- And λ3=35k
To express them in whole numbers, we can multiply through by 15 (the least common multiple of the denominators):
- λ1=9
- λ2=5
- λ3=3
Thus, the final ratio is:
λ1:λ2:λ3=15:9:5
Final Answer
The ratio of wavelengths λ1:λ2:λ3 is 15:9:5.
---
For a closed organ pipe, the fundamental frequency (first harmonic) has one node at the closed end and one antinode at the open end. The wavelengths for the fundamental and overtones can be described as follows:
- Fundamental (1st harmonic): λ1=4L
- First overtone (2nd harmonic): λ2=4L3
- Second overtone (3rd harmonic): λ3=4L5
From the resonance conditions:
1. For the fundamental mode:
L=λ14⇒λ1=4L
2. For the first overtone:
L=3λ24⇒λ2=4L3
L=5λ34⇒λ3=4L5
Now we can find the ratios of the wavelengths:
- From the equations derived:
- λ1=4L
- λ2=4L3
- λ3=4L5
λ1λ2=4L4L3=3
λ2λ3=4L34L5=53
We can combine these ratios:
- Let λ1:λ2=3:1
- Let λ2:λ3=5:3
- Let λ2=1k
- Then λ1=3k
- And λ3=35k
- λ1=9
- λ2=5
- λ3=3
λ1:λ2:λ3=15:9:5
The ratio of wavelengths λ1:λ2:λ3 is 15:9:5.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT
62 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Subjective Questions
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf I1,I2andI3 are wave lengths of the waves giving resonance with fundamental, first and second over tones of closed organ pipe. The ratio of wavelengths I1:I2:I3 is.....
View Solution
Knowledge Check
If alpha particle, proton and electron move with the same momentum, them their respective de Broglie wavelengths λα,λp,λe are related as
Aλα=λp=λeBλα<λp<λeCλα>λp>λeDλp>λe>λα
If λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1:λ2 is
View SolutionIf λ1 and λ2 are the wavelengths of the first members of the Lyman and paschen series respectively, then λ1λ2 is equal to
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View Solution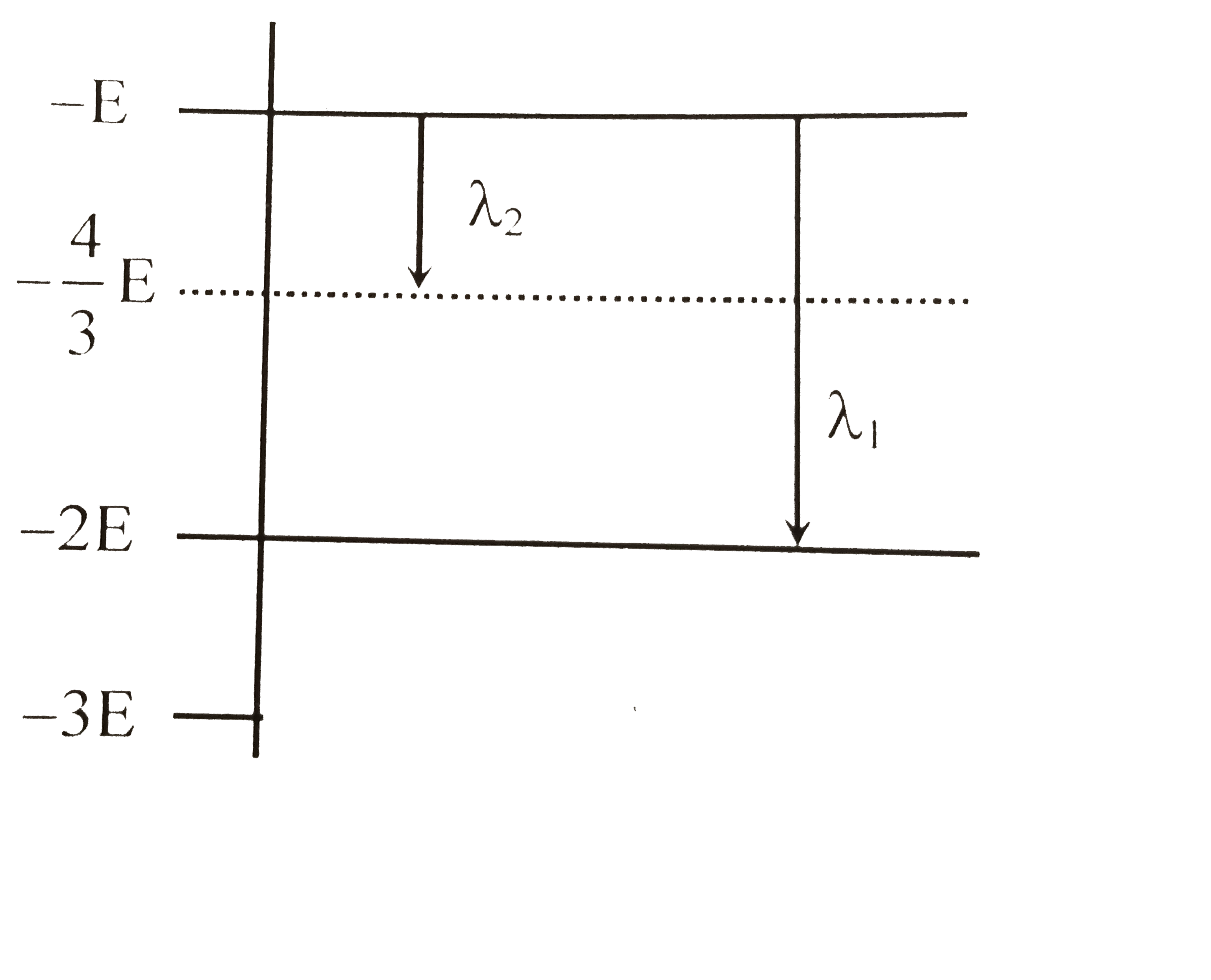
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionThe ration of resolving powers of an optical microscope for two wavelangths
λ1=4000 Åandλ2=6000Åis
View SolutionIf λ1 and λ2 denote the wavelength of de Broglie waves for electrons in the first and second Bohr orbits in a hydrogen atom, the λ1λ2 is equal to
View Solution
