In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
(ln2)LR
0.5LR
√2LR
(√2√2−1)LR
The correct Answer is:A
To solve the problem of finding the time after which the energy stored in the inductor of a decaying L-R circuit reduces to one fourth of its initial value, we can follow these steps:
1. Understand the Initial Energy Stored in the Inductor:
The energy U stored in an inductor is given by the formula:
U=12LI2
where L is the inductance and I is the current through the inductor. The initial current in the circuit is denoted as I0.
2. Set Up the Equation for One Fourth Energy:
The initial energy stored in the inductor is:
U0=12LI20
We need to find the time t when the energy reduces to one fourth of its initial value:
U=14U0=14(12LI20)=18LI20
3. Relate Current to Energy:
The energy at time t can also be expressed in terms of the current I(t):
U(t)=12LI(t)2
Setting this equal to one fourth of the initial energy, we have:
12LI(t)2=18LI20
Simplifying, we find:
I(t)2=14I20
Taking the square root gives:
I(t)=I02
4. Current Decay in an L-R Circuit:
The current in an L-R circuit decays according to the equation:
I(t)=I0e−tτ
where τ=LR is the time constant of the circuit.
5. Set Up the Equation:
Now, substituting I(t)=I02 into the decay equation:
I02=I0e−tτ
Dividing both sides by I0 (assuming I0≠0):
12=e−tτ
6. Take the Natural Logarithm:
Taking the natural logarithm of both sides:
ln(12)=−tτ
This simplifies to:
−ln(2)=−tτ
Therefore:
t=τln(2)
7. Substitute for τ:
Since τ=LR:
t=LRln(2)
Final Answer:
The time after which the energy stored in the inductor reduces to one fourth of its initial value is:
t=LRln(2)
The energy U stored in an inductor is given by the formula:
U=12LI2
where L is the inductance and I is the current through the inductor. The initial current in the circuit is denoted as I0.
The initial energy stored in the inductor is:
U0=12LI20
We need to find the time t when the energy reduces to one fourth of its initial value:
U=14U0=14(12LI20)=18LI20
The energy at time t can also be expressed in terms of the current I(t):
U(t)=12LI(t)2
Setting this equal to one fourth of the initial energy, we have:
12LI(t)2=18LI20
Simplifying, we find:
I(t)2=14I20
Taking the square root gives:
I(t)=I02
The current in an L-R circuit decays according to the equation:
I(t)=I0e−tτ
where τ=LR is the time constant of the circuit.
Now, substituting I(t)=I02 into the decay equation:
I02=I0e−tτ
Dividing both sides by I0 (assuming I0≠0):
12=e−tτ
Taking the natural logarithm of both sides:
ln(12)=−tτ
This simplifies to:
−ln(2)=−tτ
Therefore:
t=τln(2)
Since τ=LR:
t=LRln(2)
The time after which the energy stored in the inductor reduces to one fourth of its initial value is:
t=LRln(2)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Comprehension Based
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Subjective
21 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Let C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
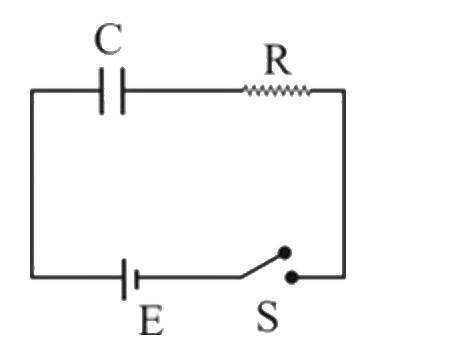
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
View SolutionFor L-R circuit, the time constant is equal to
View SolutionAn LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε . Find the time taken for the magnetic energy stored in the circuti to change from one fourth of the steady state value to half of the steady stae value.
View SolutionFind the time after which current in the circuit becomes 80% of its maximum value
View SolutionA simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
View SolutionIn an LR circuit connected to a battery, the rate at which energy is stored in the inductor is plotted against time during the growth of current in the circuit. Which of the following best represents the resulting curve?
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
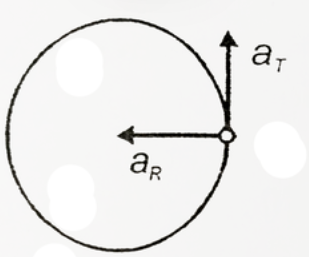
The time after which the speed of particle reduces to half of its initial value is
View SolutionThe energy stored in an inductor of self inductance L carrying current l, is given by
View SolutionThe electron in a hydrogen atom jumps from ground state to the higher energy state where its velcoity is reduced to one-third its initial value. If the radius of the orbit in the ground state is r the radius of new orbit will be
View Solution
