In C−R circuit, answer the following two questions
During charging of C−R circuit let t1 and i1 be the time constant and initial charging current when capacitor is assumed to be filled by a perfect insulator and t2 and i2 be the corresponding values when it is assumed imperfect. Then
t1<t2
i1>i2
Both (a) and (b) are correct
Both (a) and (b) are wrong
The correct Answer is:C
Step by step video & image solution for In C - R circuit, answer the following two questions During charging of C - R circuit let t_(1) and i_(1) be the time constant and initial charging current when capacitor is assumed to be filled by a perfect insulator and t_(2) and i_(2) be the corresponding values when it is assumed imperfect. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching2videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced44videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery21videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
Similar Questions
Current growth in two L-R circuits (b) and (c ) as shown in figure (a). Let L1,L2,R1 and R2 be the corresponding values in two circuits. Then
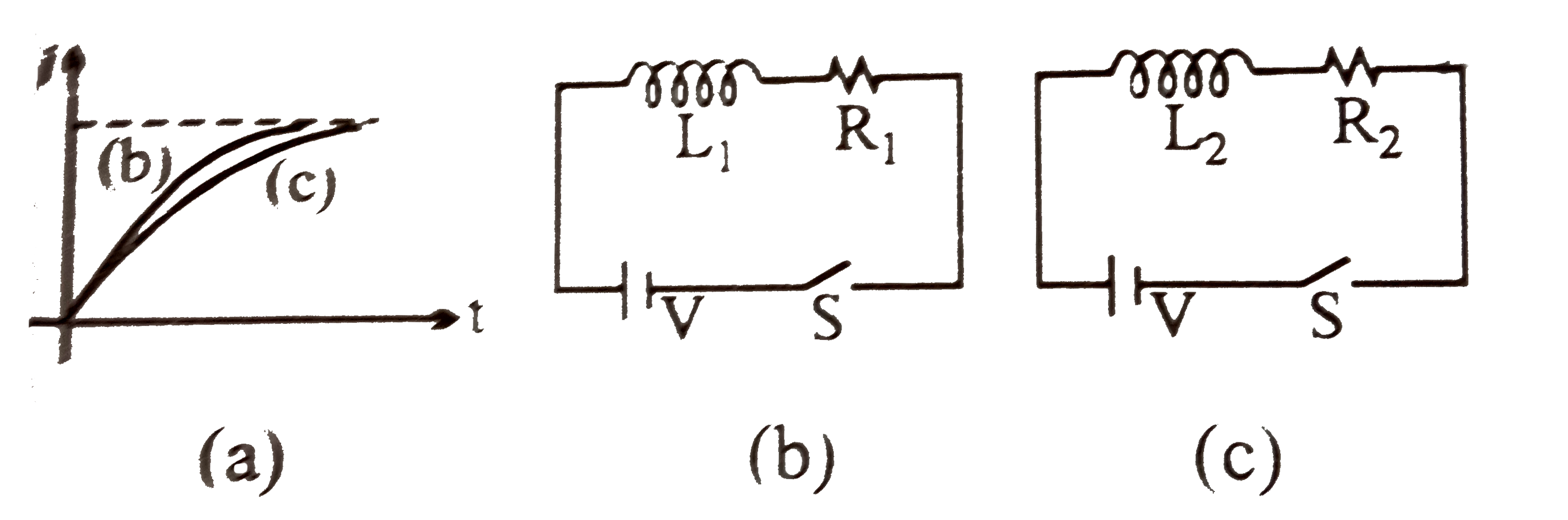
View SolutionIn charging singe loop R - C circuit, after how many time constant, the potential energy in the capacitor will be 25% of its maximum value.
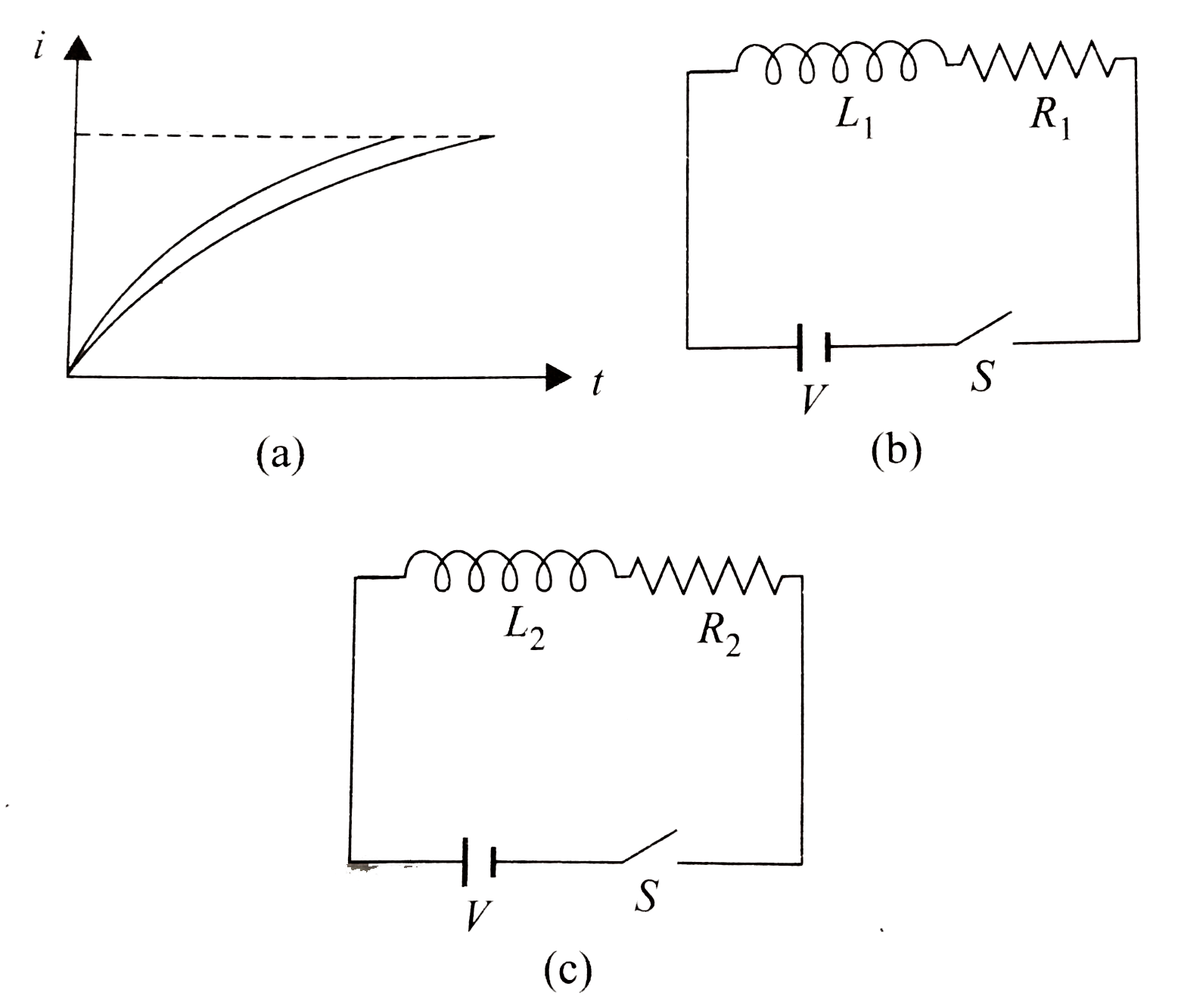
View SolutionThe current growth in two L-R circuits (b) and (c) is as shown in Fig. Let L1,L2,R1andR2 be the corresponding values in two circuits. Then
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionIn the given circuit find the ratio of i1toi2. Where is the initial (at t=0) current, and i2 is steady state (att=∞) current the battery
View SolutionTime constant of a C-R circuit is 2ln(2) second. Capacitor is discharged at time t=0. The ratio of charge on the capacitor at time t=2s and t=6s is
View SolutionThe following two questions refer to the circuit shown. Assume that the capacitors are initially uncharged.
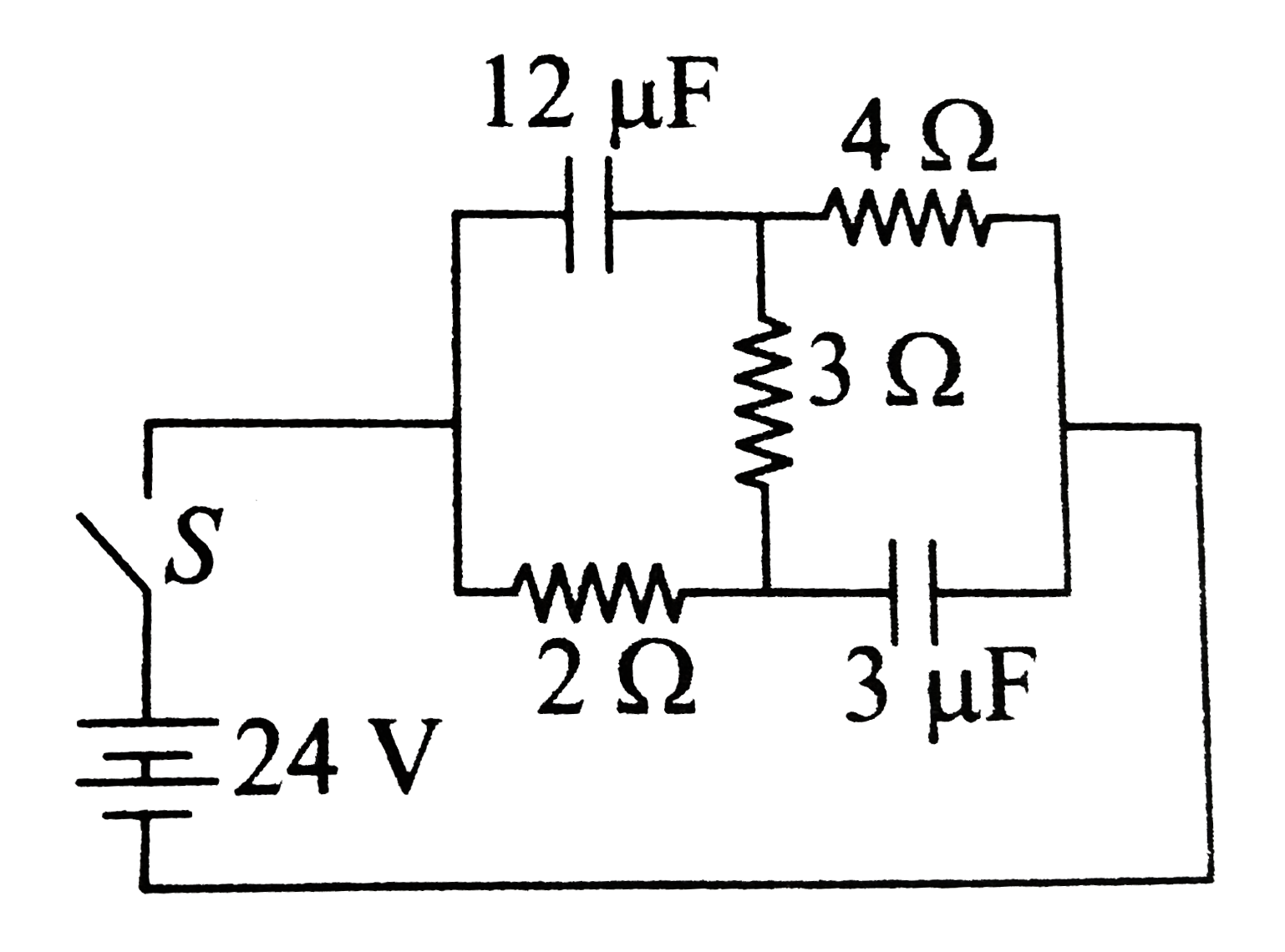
At time t = 0, the switch S in the circuit is closed. At that instant, what is the equivalent resistance of the circuit?View SolutionIn a cirtain circuit current changes with time according to i=√t. Average value of current betweent=1 to t=2s is about to
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
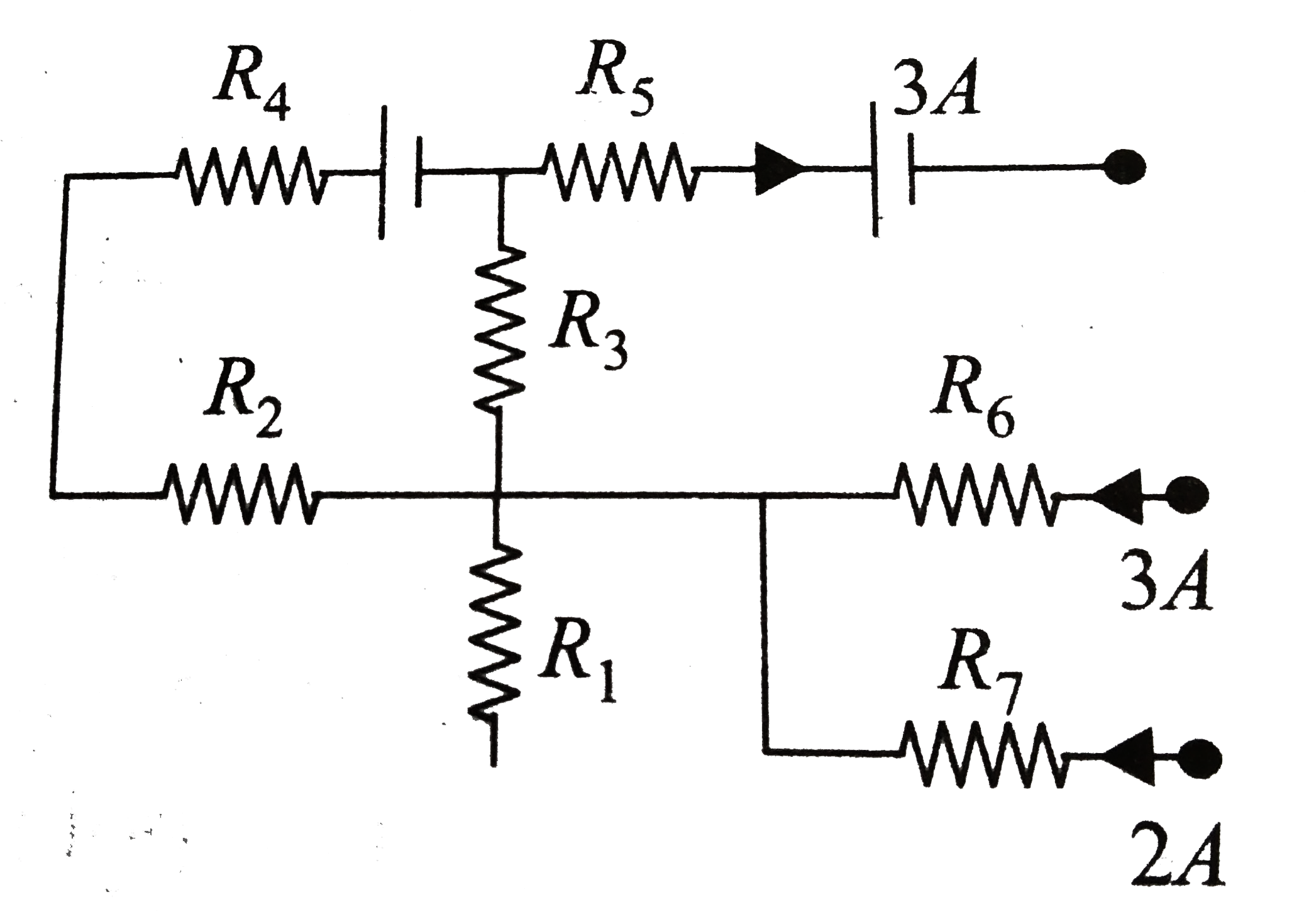. View SolutionThe following two questions refer to the circuit shown. Assume that the capacitors are initially uncharged.
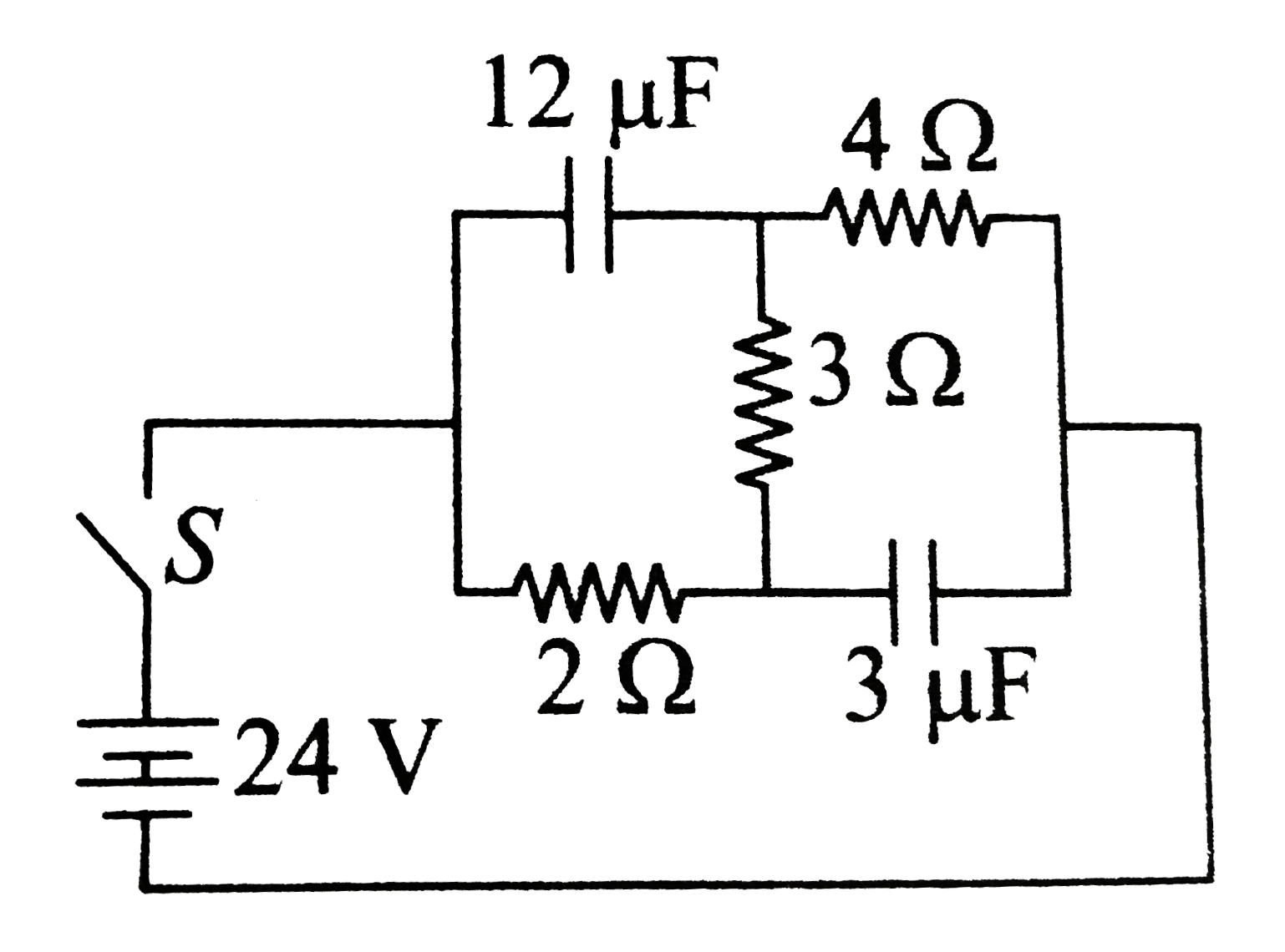
After the switch has been closed for a long time, how much charge is on the positive plate of the 3μF capacitor?View Solution