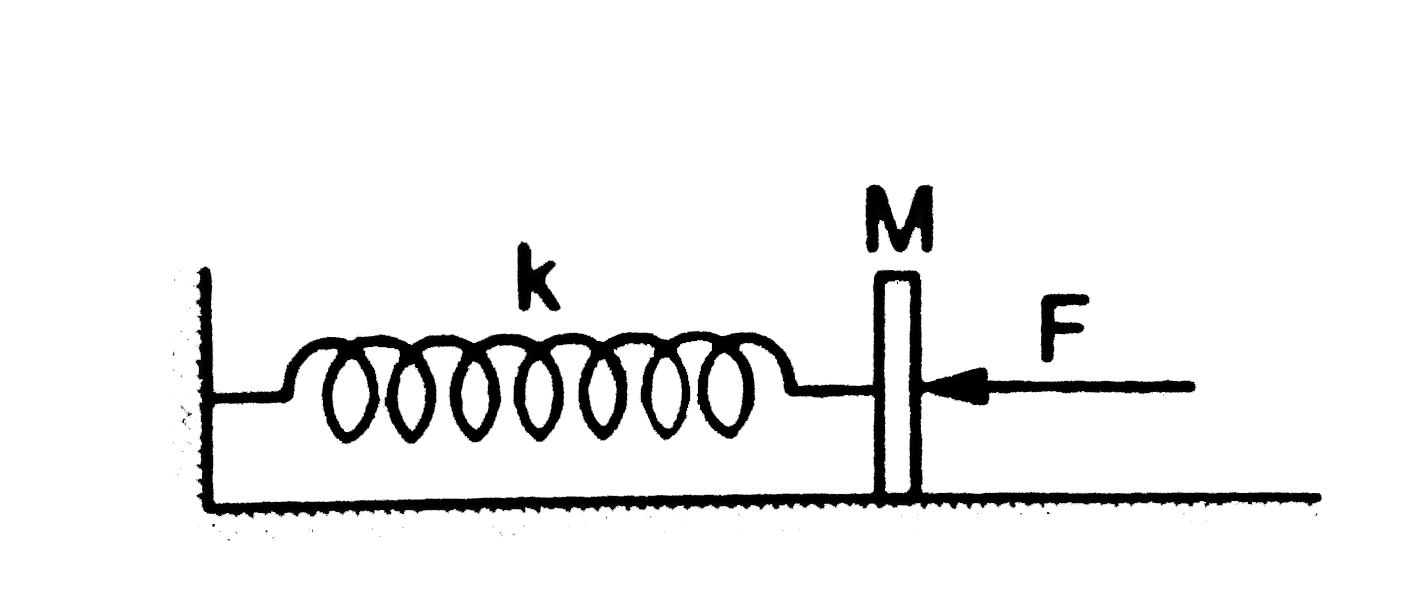
In figue $k = 100 N m^{- 1} M = 1 k g and F = 10 N$ . a. Find the compression of the spring in the equilibrium position. b. A sharp blow by some xternal agent imparts a speed of $2 m s^{- 1}$ to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at ths instant. c. find the time period of the resulting simple harmonic motion. d. Find the ampitude. e. Write the potential energy of the spring when the block is at the left extreme. f. Write teh potential energy of the spring when teh block is at the right extreme.
The anwer of b, e, and f are different. Explain why this does not violate the principle of conservation of energy.

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

Given $k = 100 B \frac{N}{m}, m = 1 k g and F = 10 N < b r > a . I n t h e e q u i l i b r i u m p o s i t i o n < b r >$ Compression $= δ = \frac{F}{k} = \frac{10}{100}$
$= 0.1 m = 10 c m$
b. The below imparts a speed of 2 m/s to the block towards left.
$∴ + P . E . + K . E . = \frac{1}{2} k δ^{2} + \frac{1}{2} M v^{2}$
$= \frac{1}{2} x 100 \times {(0.1)}^{2} + \frac{1}{2} x 1 \times 4$
$= 0.5 + 2 = 2.5 J$
$c . T i m e p e r i o d$ 2pisqrt(M/k) $< b r >$ =2pi sqrt(M/100)=pi/5 sec $< b r > d . L e t t h e a m p l i t u d e b e x w h i g h m e a n s t h e d i s t a s n c e b e t w e n t h e m e a n p o s i t i o n and t h e e x t r e m e p o s i t i o n . < b r > S o \in t h e e x t r e m e p o s i t i o n, c o m p r e s s i o n o f t h e s p r \in g i s$ (x-K) $< b r > Sin c e \in S H M t h e \to t l e \neq r g y r e m a \in s c o n s tan t, < b r >$ 1/2k(x+delta)^2=1/2kdelta^2+1/2mv^2+Fx $< b r >$ =2.5+10x
[because 1/2kdelta^2+1/2mv^2=2.5] $< b r > s o,$ 50(x+0.1)^2=2.5+10x $< b r >$ :. 50x^2+0.5+10x=2.5+10x $< b r >$ =:. 50x^2=2 $< b r >$ rarr x^2=2/50=4/100 $< b r >$ rarr x=2/50x=20m $< b r > e . p o t e n t i a l e \neq r g y a t t h e \leq f t e x t r e m e i s g i v e n b y < b r >$ P.E. =1/2k(x+delta)^2 $< b r >$ =1/2x100xx(0.1+0.2)^2 $< b r >$ =50xx(0.09)=4.5J $< b r > f . P o t e n t i a l e \neq r g y a t t h e r i g h t e x t r e m e i s g i v e n b y < b r >$ P.E. 1/2k(x+delta)^2-F(2x) $< b r >$ [2x $= d i s tan c e b e t w e e n t w o e x t r e m e)$
$= 4.5 - 10 (0.4) = 0.5 J$
The different values is b, e, and f do not violate law of conservastion of energy as the work is done by the exterN/Al force 10 N.

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

HC VERMA-SIMPLE HARMONIC MOTION-Exercises

Home
Ask Doubt
Profile