In problem 9 the acceleration of the particle is
10πm and 5πms2
5πm and 5π2ms2
10πm and 5π2ms2
5πm and 5π4ms2
The correct Answer is:C
To solve the problem regarding the acceleration of a particle in simple harmonic motion, we can follow these steps:
1. Identify the Given Values:
- Maximum displacement (amplitude), A=10/π meters.
- Angular frequency, ω=π2 radians/second.
2. Use the Formula for Maximum Acceleration:
The maximum acceleration amax in simple harmonic motion is given by the formula:
amax=ω2A
3. Substitute the Values into the Formula:
- First, calculate ω2:
ω2=(π2)2=π24
- Now substitute ω2 and A into the acceleration formula:
amax=π24⋅10π
4. Simplify the Expression:
- Simplifying the expression:
amax=10π24π=10π4=5π2 m/s2
5. Conclusion:
- The maximum acceleration of the particle is:
amax=5π2 m/s2
Final Answer:
The maximum acceleration of the particle is 5π2 m/s2.
---
- Maximum displacement (amplitude), A=10/π meters.
- Angular frequency, ω=π2 radians/second.
The maximum acceleration amax in simple harmonic motion is given by the formula:
amax=ω2A
- First, calculate ω2:
ω2=(π2)2=π24
- Now substitute ω2 and A into the acceleration formula:
amax=π24⋅10π
- Simplifying the expression:
amax=10π24π=10π4=5π2 m/s2
- The maximum acceleration of the particle is:
amax=5π2 m/s2
The maximum acceleration of the particle is 5π2 m/s2.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Assertion Reasoning
Explore 6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
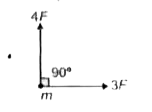
When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
View SolutionA pulley is attached to the celing of a lift moing upwards. Two particles are attached to the two ends of a stirng passing over the pulley. The masses of the particles are in the ration 2:1 if the acceleration of the particles is g/2, then the acceleration of the lift will be
View Solution
Knowledge Check
In the question number 35, the acceleration of the particle at t=1 is
A2ˆjms−2B−2ˆjms−2C4ˆjms−2D−4ˆjms−2A particle revolves round a circular path with uniform speed. The acceleration of the particle is
Aalong the circumference of the circle.Balong the tangentCalong the radiusDzero
Starting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionA particle of mass m moves along a curve y=x2. When particle has x-coordinate as 12 m and x-component of velocity as 4ms, then
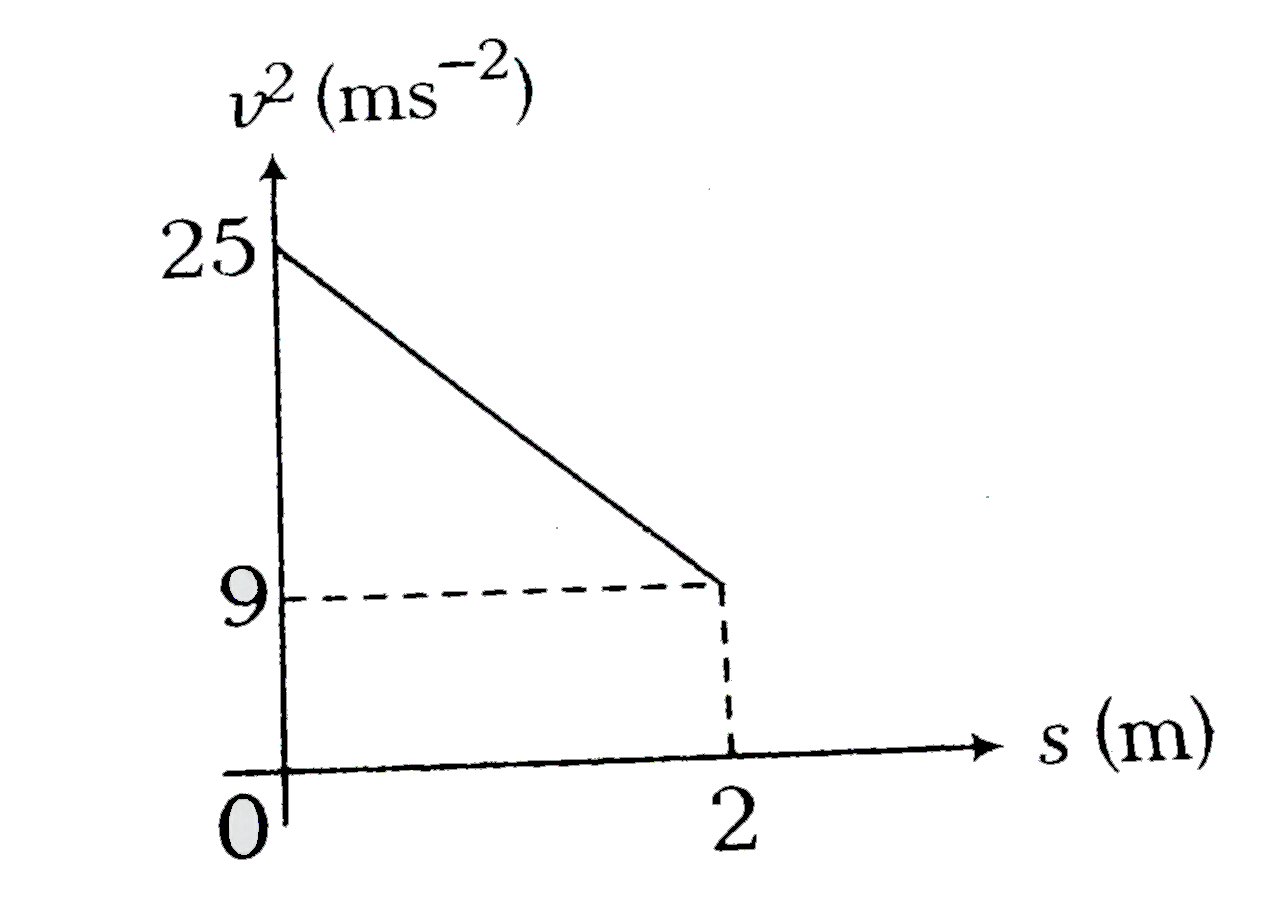
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
View SolutionA particle moves in a circle of radius 25 cm at 2 revolution per second. The acceleration of the particle in meter per second2 is
View SolutionA graph between the square of the velocity of a particle and the distance(s) moved is shown in figure. The acceleration of the particle in kilometers per hour square is:-

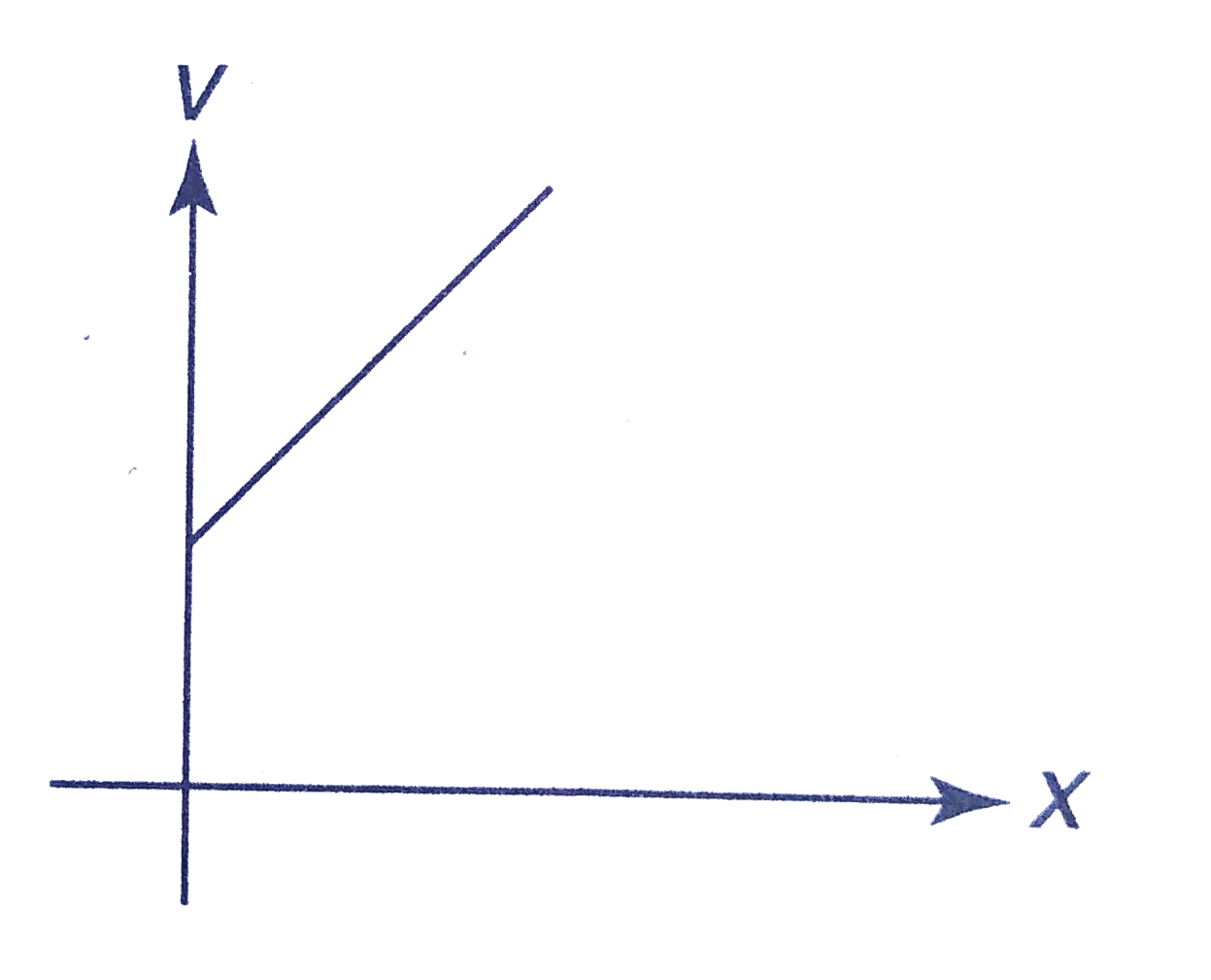
View SolutionGraph of velocity versus displacement of a particle moving in a straight line is as shown in figure.
The acceleration of the particle is.
View Solution