In problem 11446787 the maximum displacement and acceleration of the particle are respectively:
5√3π2ms
5π22ms2
5√3π4ms2
5√3ms2
The correct Answer is:C
From the graph T=(5−1)=4s
(distance between the two adjacent shown in the figure)
and vmax=5ms,ωA=5ms
(2πT)A=5⇒A=5T2π=5×42π=10π m
Also ω=2π4=π2rads
The equation of velocity can be written as
v=5sin(π2)tms
At extreme position, v=0, sin(π2)t=0 or t=2s
Phase of the particle velocity at that insstant corresponding to the above equation =π
Therefore, when a phase change of π5 takes place, the resulting phase=π+π6
v=5sin(π+(π)6)=−5sin(π6)=−5(12)
=2.5ms (numerically)
dydt=v⇒dy=dt
dy=∫5sin(πt2)dt=10π[−cos(πt2)]+C
Since at t=0, the particle is at the extreme position, there fore at r=0,y=−10π
−10π=−10πcosθ+C⇒C=0
y=−10πcos(πt2)
Clearly a phase change of π6 corresponds to a time difference of T2π(π6)=T12=412=13s
y=−10πcos(π6)=−10π(√32)
=5√3πm (numerically)
Acceleration a=dvdt=ddt(5sin(πt2))=5π2cosπt2
a at t=13s=5π2cos(π6)=5π√34ms2
Maximum displacement xmax=A=10πm
and maximum accceleration, amax=ω2A
=(π2)2×10π=5π2ms2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2
The phase difference between displacement and acceleration of particle in a simple harmonic motion is
View SolutionIn the above problem the displacement after 2 s is:
View SolutionFollowing are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s)
View SolutionA sinusoidal wave propagates along a string. In figure (a) and (b) 'y' represents displacement of particle from the mean postion. 'x' & 't' have usual meanings. Find :-
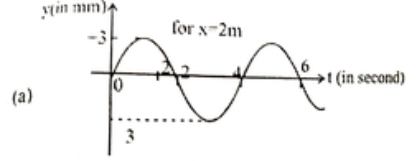
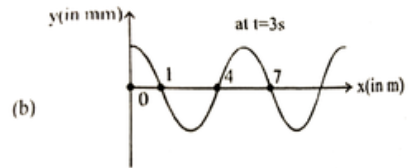
(a) wavelength, frequency and speed of the wave
(b) maximum velocity and maximum acceleration of the particlesView SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionA particle executes linear. If a and v donate the acceleration and velocity of the particle respectively, then correct graph relating the values a2 and v2 is
View SolutionObtain the formulae for displacement, velocity, acceleration and time period of a particle executing simple harmonic motion. When is the velocity of particle maximum and when zero ? Acceleration ?
View Solution

