In the figure given in the text if mass of the rod is m then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
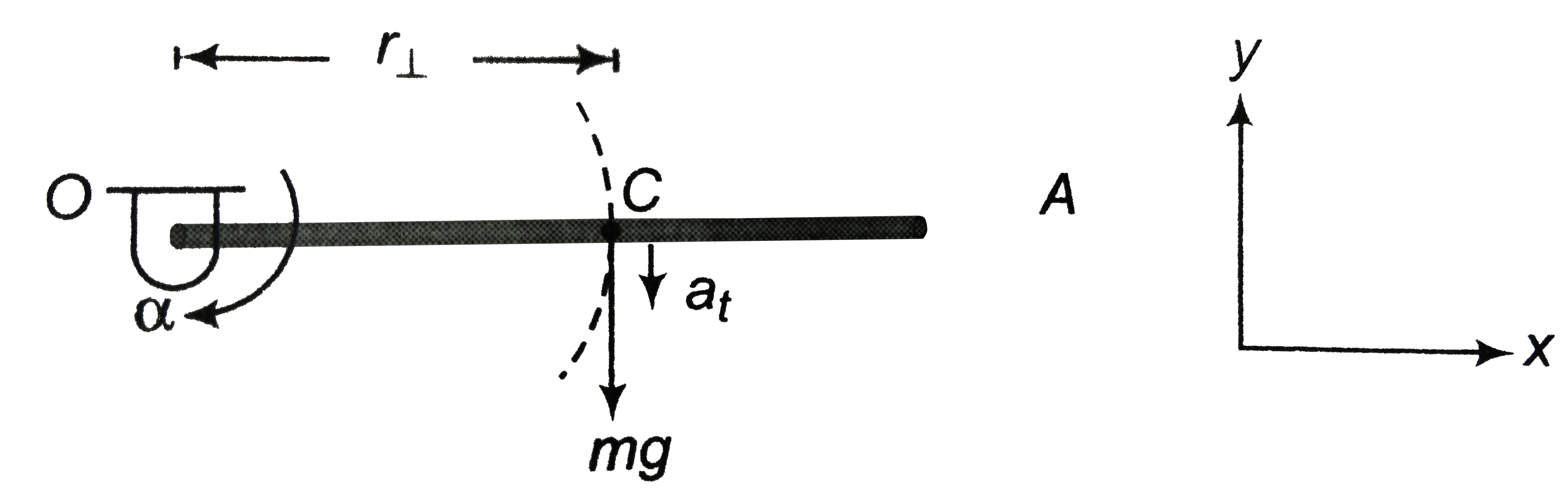

(a).
Just after the release ω=0
∴ar=rω2=0
α=τmgI
=(mg)(r⊥)I0=(mg)(l2)(ml2/3)=32gl
at=rα=(l2)(32gl)=34g
From eq (iii) the hinge force is
F=m(ac−g)
=m[at(ˆj)−(−gˆj)]
=m[−34gˆj+gˆj]
=mg4ˆj
Therefore, hinge force is mg4 in vertically upward direction
(b). When the rod becomes vertical height fallen by centre of mass is h=l2
therefore from Eq. (i)
ω2=2mghI (I=I0=ml23)
=2mg(l2)(ml2/3)=(3gl)
ar=rω2=(l2)(3gl)=32g (towards O)
At this moment mg also passes through O. Therefore its torque about O is also zero, so from Eq, (ii)
α=0⇒at=rα=0
Now, substituting proper values in Eq. (iii). The hinge force is
F=m(ac−g)
=m[arˆj−(−gˆj)]
=m[(32g)ˆj+(g)ˆj]
=(52mg)ˆj
Therefore hinge force is 52 mg in vertically upward direction.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Two masses each of m are attached at mid point B and end point C of massless rod AC which is hinged at A. It is released from horizontal position as shown. Find the force at hinge A when rod becomes vertical.
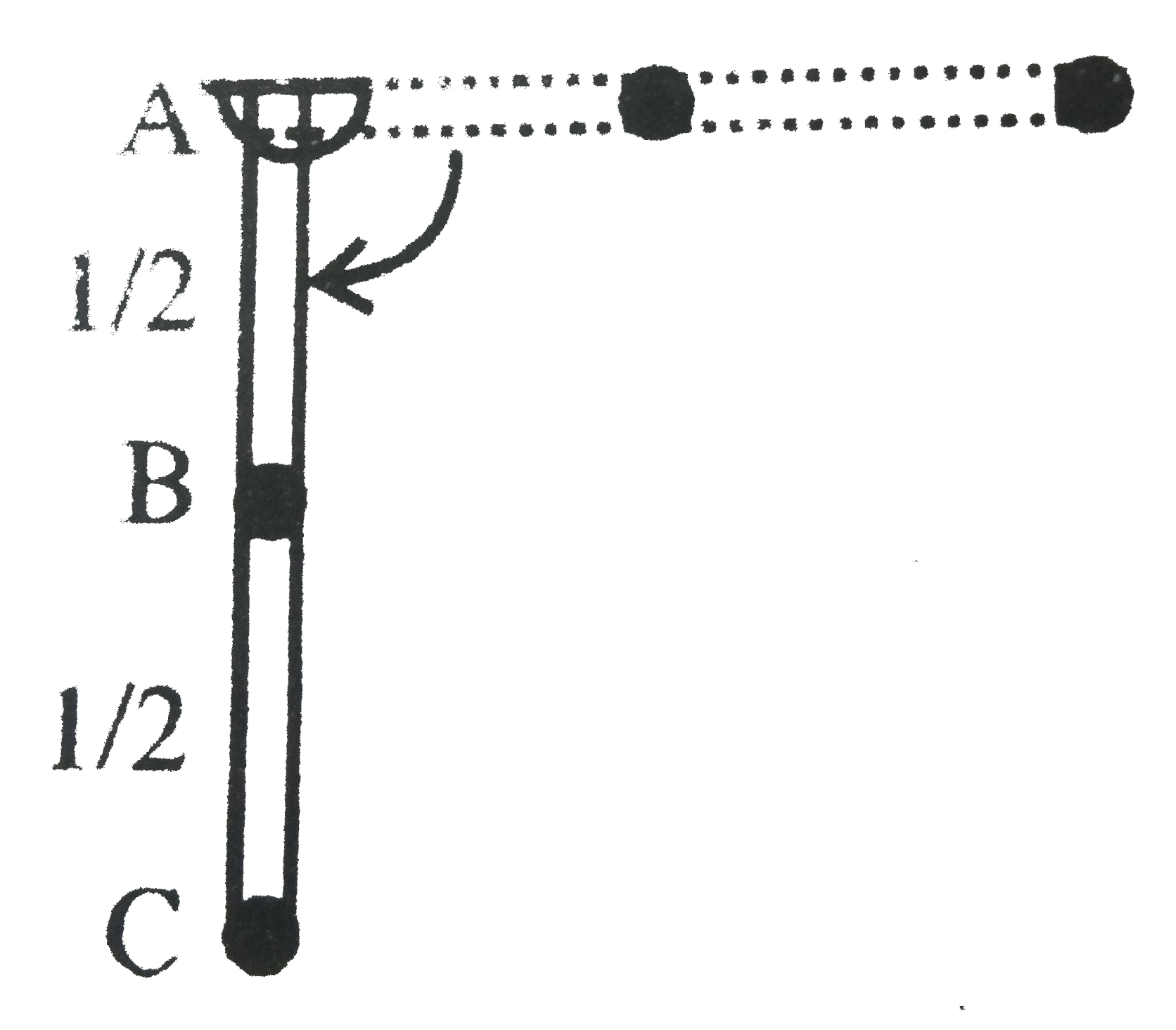 .
.
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View Solution
Knowledge Check
Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
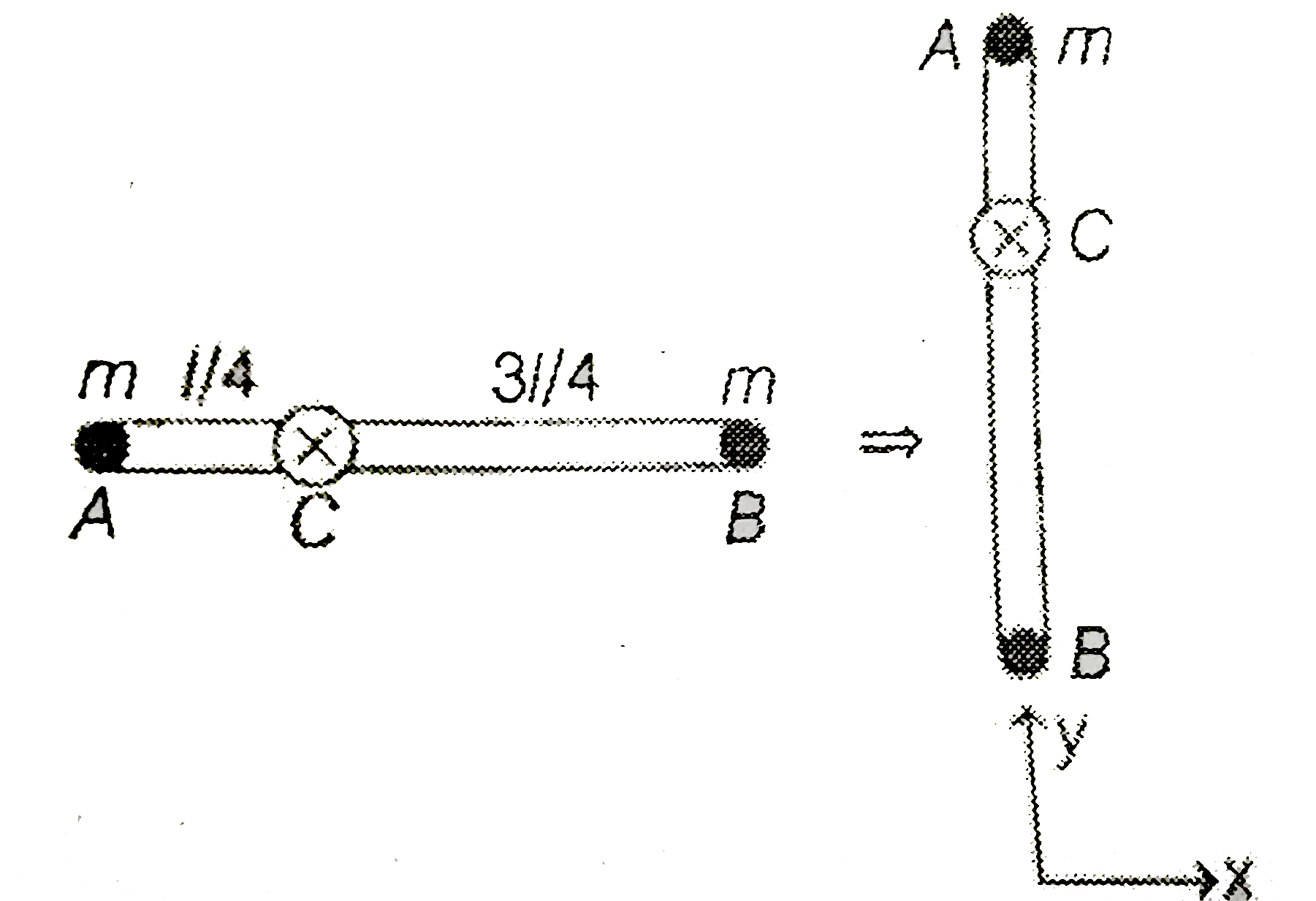 ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zeroA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mgIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass in is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical.
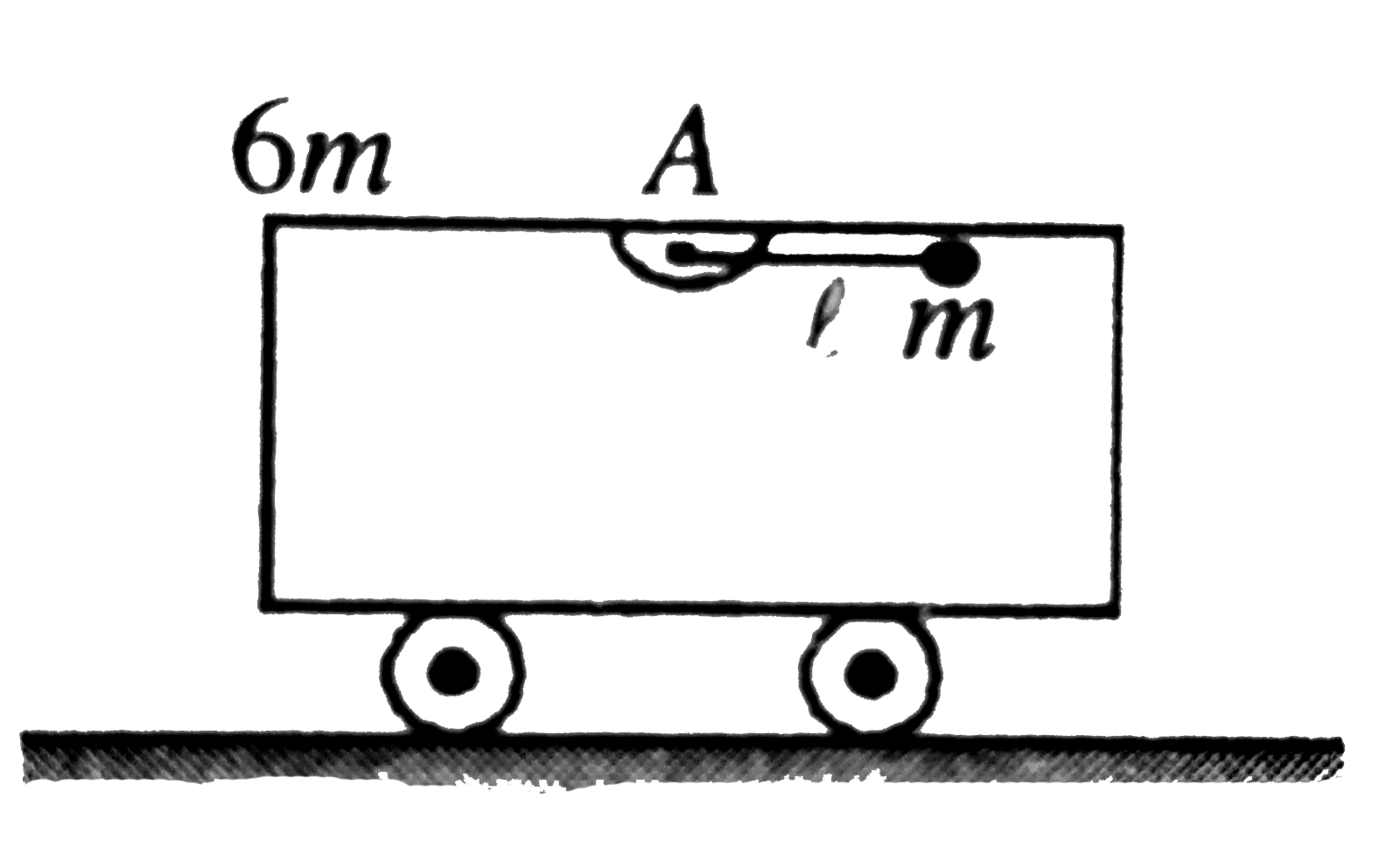 A√143glB√76glC√73glD√83gl
A√143glB√76glC√73glD√83gl
A uniform rod of length 75cm is hinged at one of its ends and is free to rotate in vertical plane. It is released from rest when rod is horizontal. When the rod becomes vertical, it is breaks at mid− point and lower part now moves freely. The distance of centre of lower part from hinge, when it again becomes vertical for the first time is r. Find the approximate value of 2r.
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity vrel of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)

View SolutionA simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

View Solution
