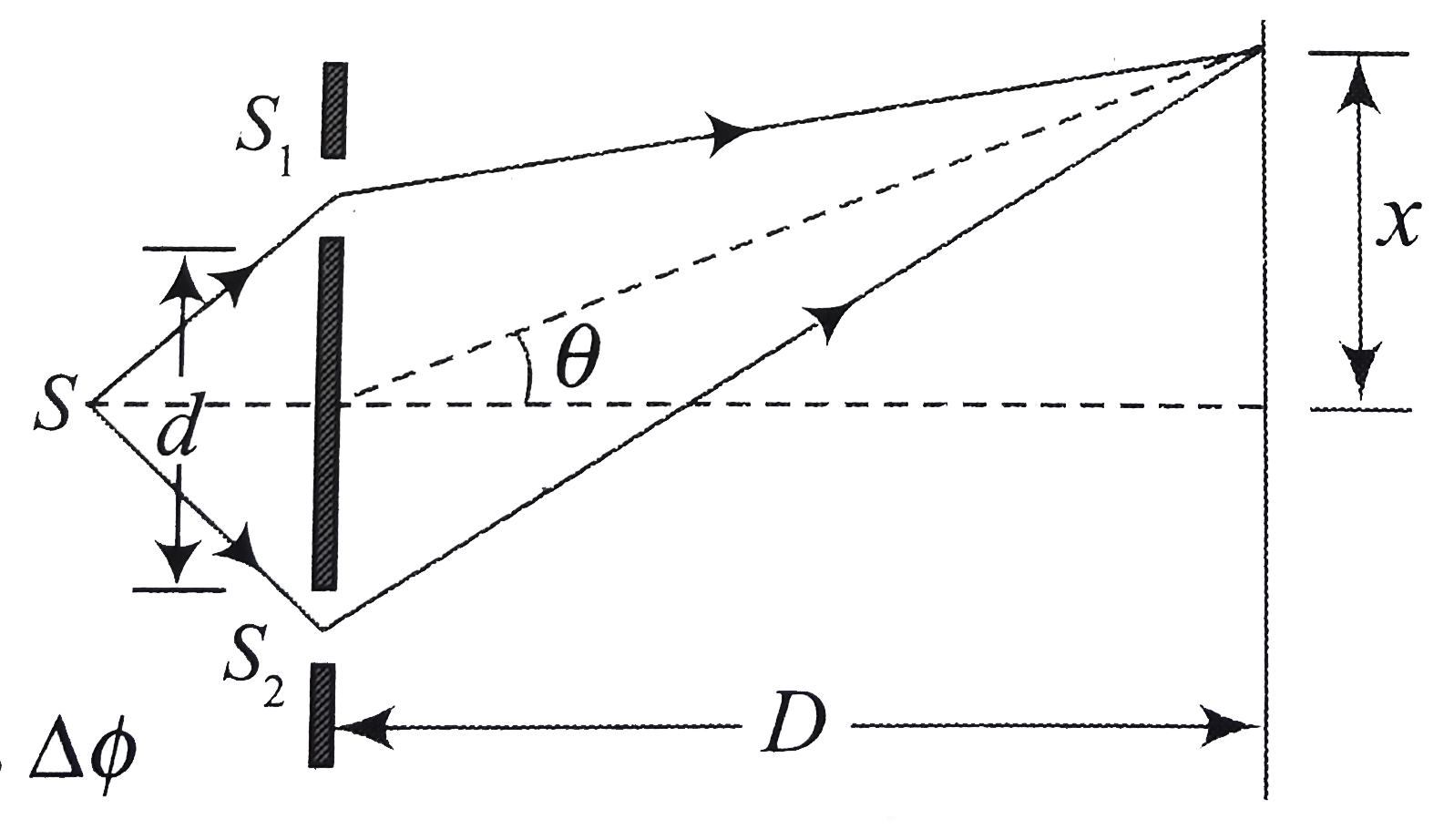
In YDSE, having slits of equal width, let β be the fringe width and I0 be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
I0cos(xβ)
I0cos2(2πxβ)
I0cos2(πxβ)
I04cos2(πxβ)
The correct Answer is:c
At point P, Δϕ=2πλΔx and Δx=dxΔ
Δϕ=2πλ×dxD=2πxβ
IP=I1+I2+2√I1I2ocsΔϕ,I1=I2=I
IP=4Icos2(Δd)2
Given 4I=I0
⇒I1=I2=I04
IP=I02+I02cosΔϕ
IP=I0cos2(Δϕ2)=I0cos2(πxβ)
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
In a Young's double slit experiment, fringe width equal to 1 mm is observed. Then the distance of the nearest bright fringe from the central fringe will be :
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe.the intensity at a distance x=4×10−5in form the central maximum is-
View Solution
Knowledge Check
In YDSE of equal width slits, if intensity at the center of screen is I0, then intensity at a distance of β/4 from the central maxima is
AI0BI02CI04DI03In a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe.the intensity at a distance x=4×10−5in form the central maximum is-
AI0BI0/2C3I0/4DI0/3In YDSE, when separation between two slits is increased, fringe width
AdecreasesBincreasesCremains the sameDnone of these
Fringe width equal to 1 mm is observed in the interference pattern of biprism experiment. Then the distance of nearest bright fringe from the central bright fringe will be :
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young’s double slit experiment, the ratio of the slit’s width is 4 : 1. The ratio of the intensity of maxima to minima, close to the central fringe on the screen, will be:
View SolutionIn Young's double slit experiment, the 10th bright fringe is at a distance x from the central fringe. Then
a) the 10th dark fringe is at a distance of 19x/20 from the central fringe
b) the 10th dark fringe is at a distance of 21x/20 from the central fringe
c) the 5th dark fringe is at a distance of x/2 from the central fringe.
d) the 5th dark fringe is at a distance of 9x/20 from the central fringe.
View SolutionIn a Young's double-slit experiment using slits of unequal widths, the intensities on the screen due to the slits are in the ratio 4:9 when the slits are used separately. When they are used together, the ratio of the intensity at a dark fringe to the intensty at a bright fringe on the screen will be
View Solution
