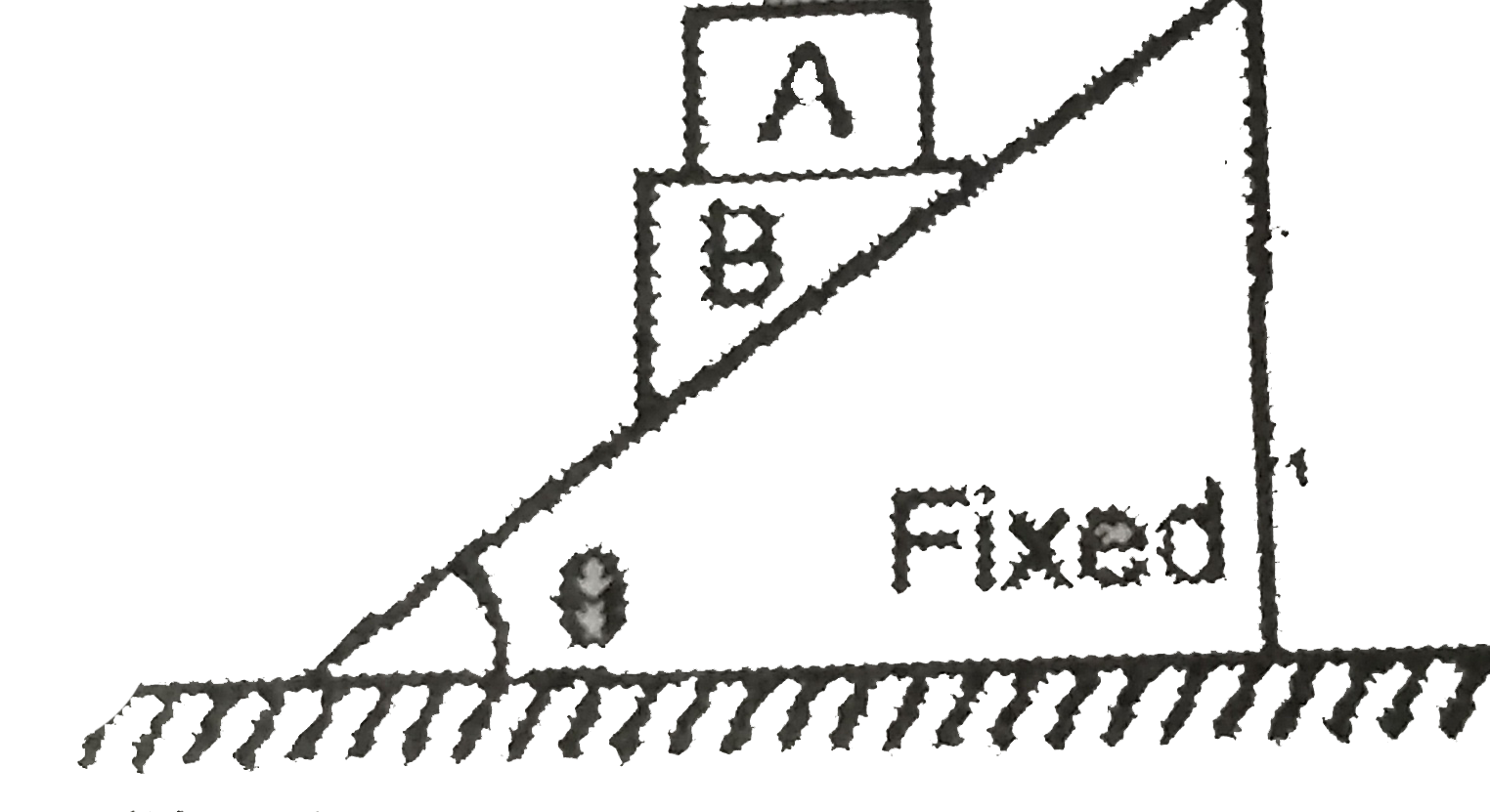
μ is coefficient of friction between all surfaces . Block A is kept over block B on inclined plane . The minimum force required such that 'A' block can accelerate along applied force is mg sin θ+nμgcosθ , calculate n .

The correct Answer is:5
Frictional force developed in all surface is limiting
F+3mgsinθ+3μmgcosθ=2T ……(i)
T−2mgsinθ−3μmgcosθ−μmgcosθ=0
T=2mgsinθ+4μmgcosθ ……(ii)
Solving the equation
F = mgsinθ+5μmgcosθ
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Matrix - Match
Explore 5 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
μ is coefficient of friction between all surface. Block A is kept of over block B on inclined plane. The minimum force required such that 'A' block can accelerate along applied force is mgsinθ+nμgcosθ calculate n.
View SolutionThe coefficient of friction between the block and the inclined plane is μ.
View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NIf coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
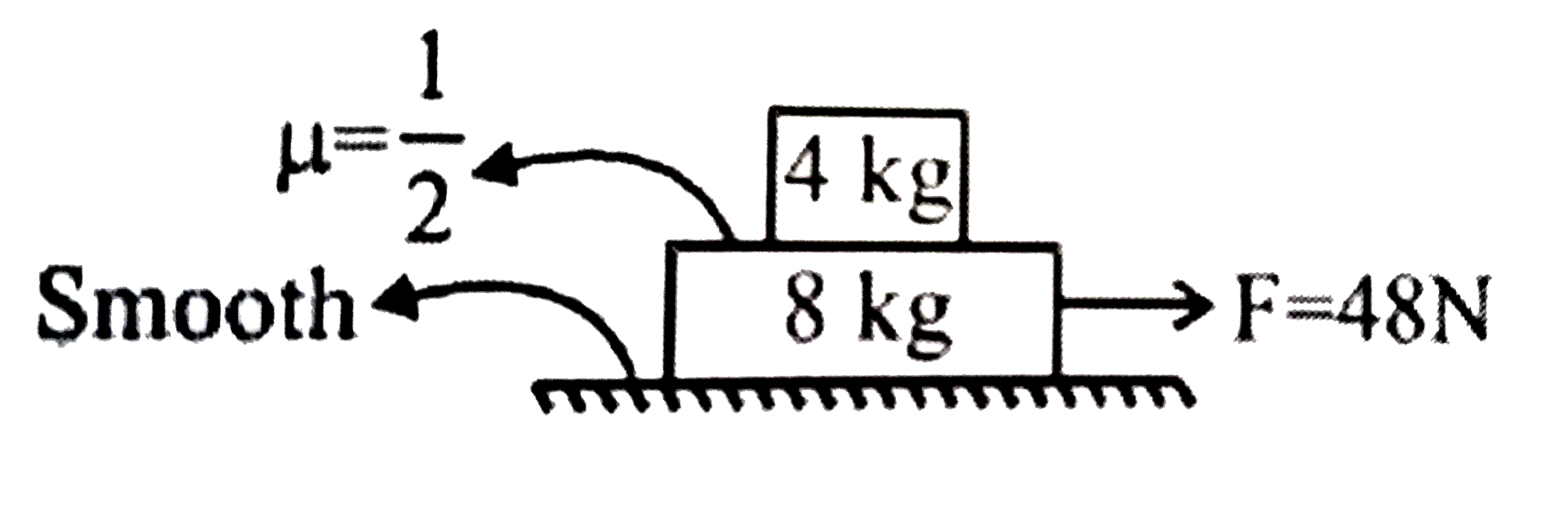 A16NB20NC8ND10N
A16NB20NC8ND10NA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
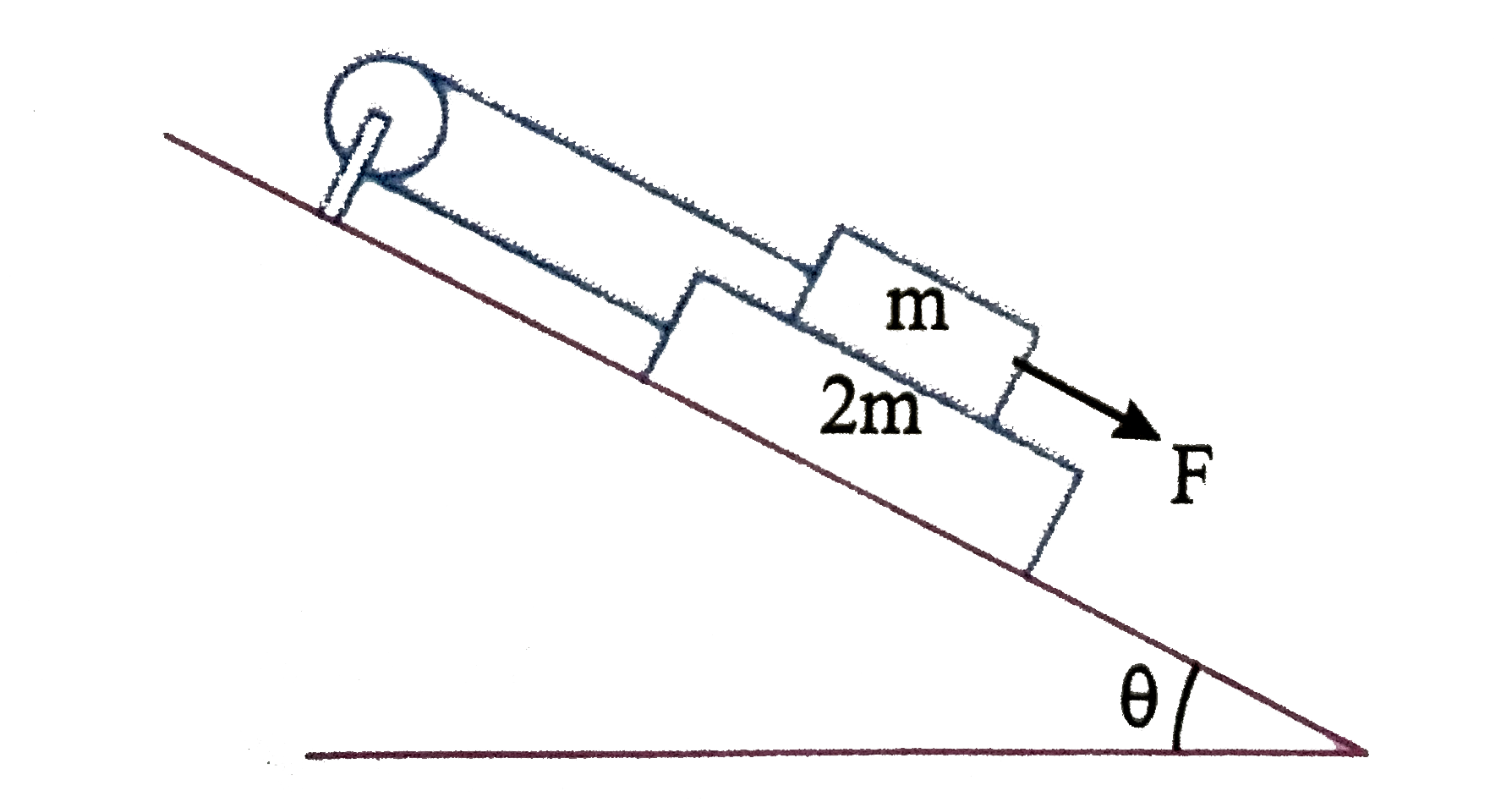
View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
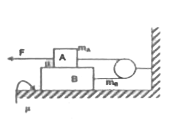
View SolutionTwo blocks A and B are lying on the table as shown in the figure. The coefficient of friciton between block A and block B is μ. The coefficient of friction between block B and ground also μ. An external force F is applied in the direction shown. The maximum value of the force F that can be applied without moving the blocks.
View SolutionA block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.

If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View Solution