ODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of per unit length. Find the current in the rotating conductor, as it rotates by .

Let us consider the position of rotating conductor at time interval
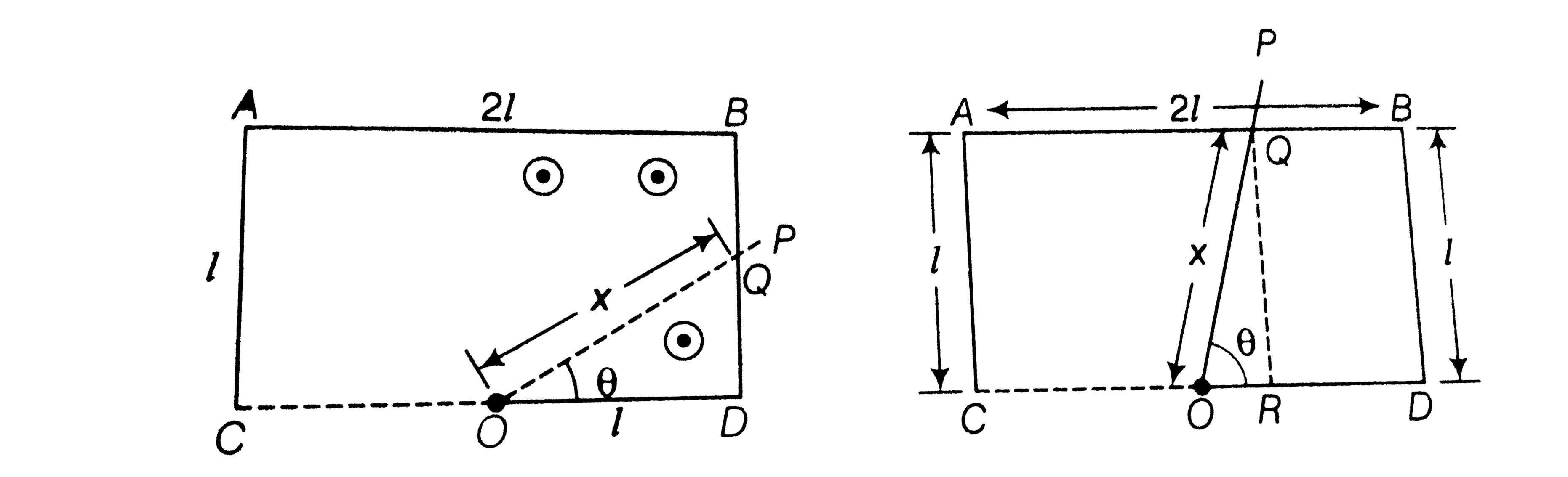
The rod OP will make contact with the side BD. Let the length OQ of the contact at sometime t such that or be . The flux through the area ODQ is
, where
Applying Faraday's law of EMI,
Thus, the current is where R is the resistance of the rod in contact.
Where,
let the length OQ of the contact at some time t such that or be x. The rod is in contact with the side AB. The flux through the area OQBD is
Where,
Thus, the magnitude of emf generated in the loop is
The current is
Similarly for or the rod will be in touch with AC.
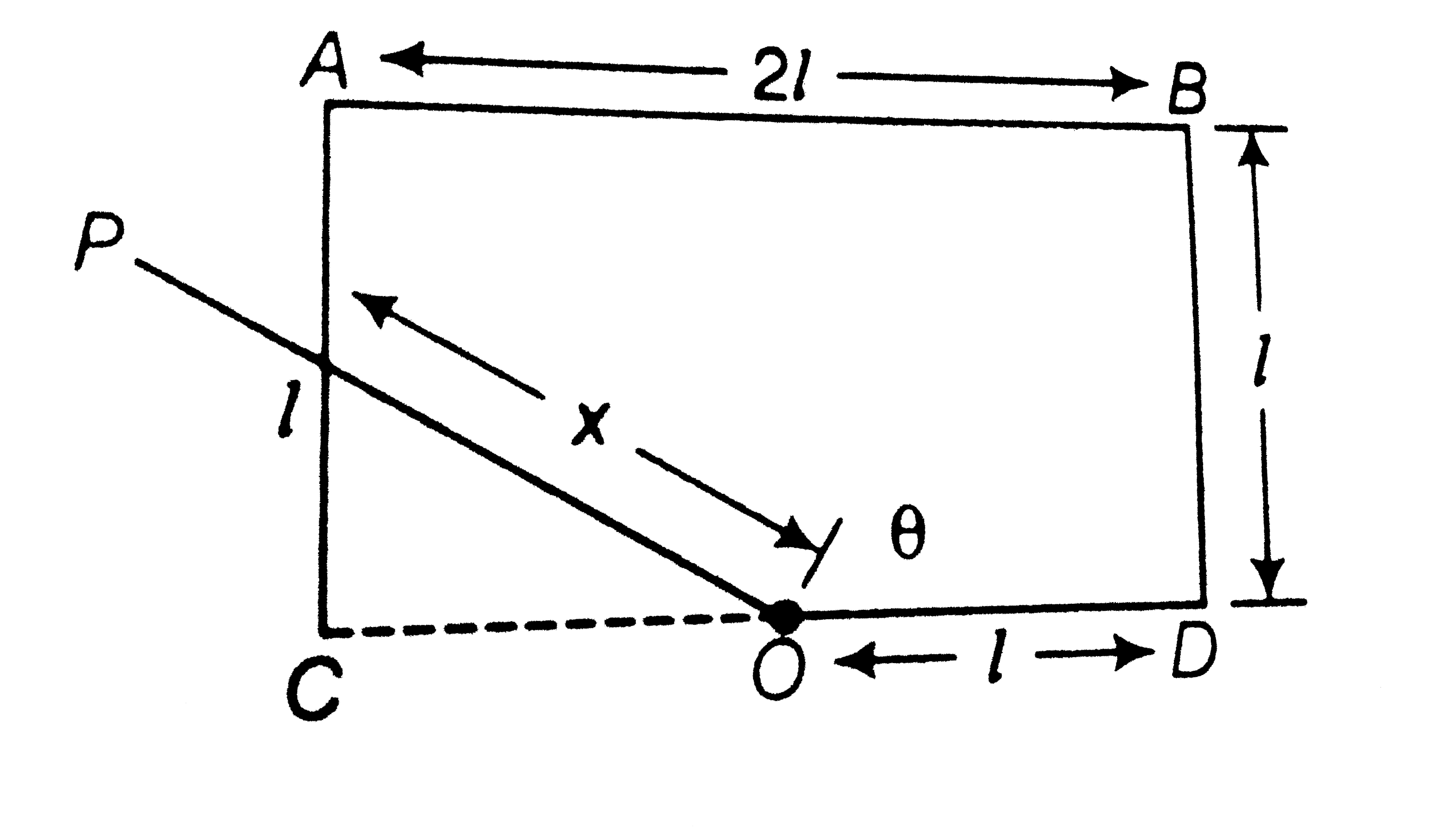
The flux through OQABD is given by
And the magnitude of emf generated in loop is given by
These are the required expressions.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Short answer type questions
5 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
Similar Questions
ODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity ω (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180∘.

View SolutionThe resistance of a conductor is
View Solution
Knowledge Check
A circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is 4ω. The net magnetic field at the centre of the conductor is
 Aμ02B8μ03C2μ0Dzero
Aμ02B8μ03C2μ0DzeroTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward with a constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)
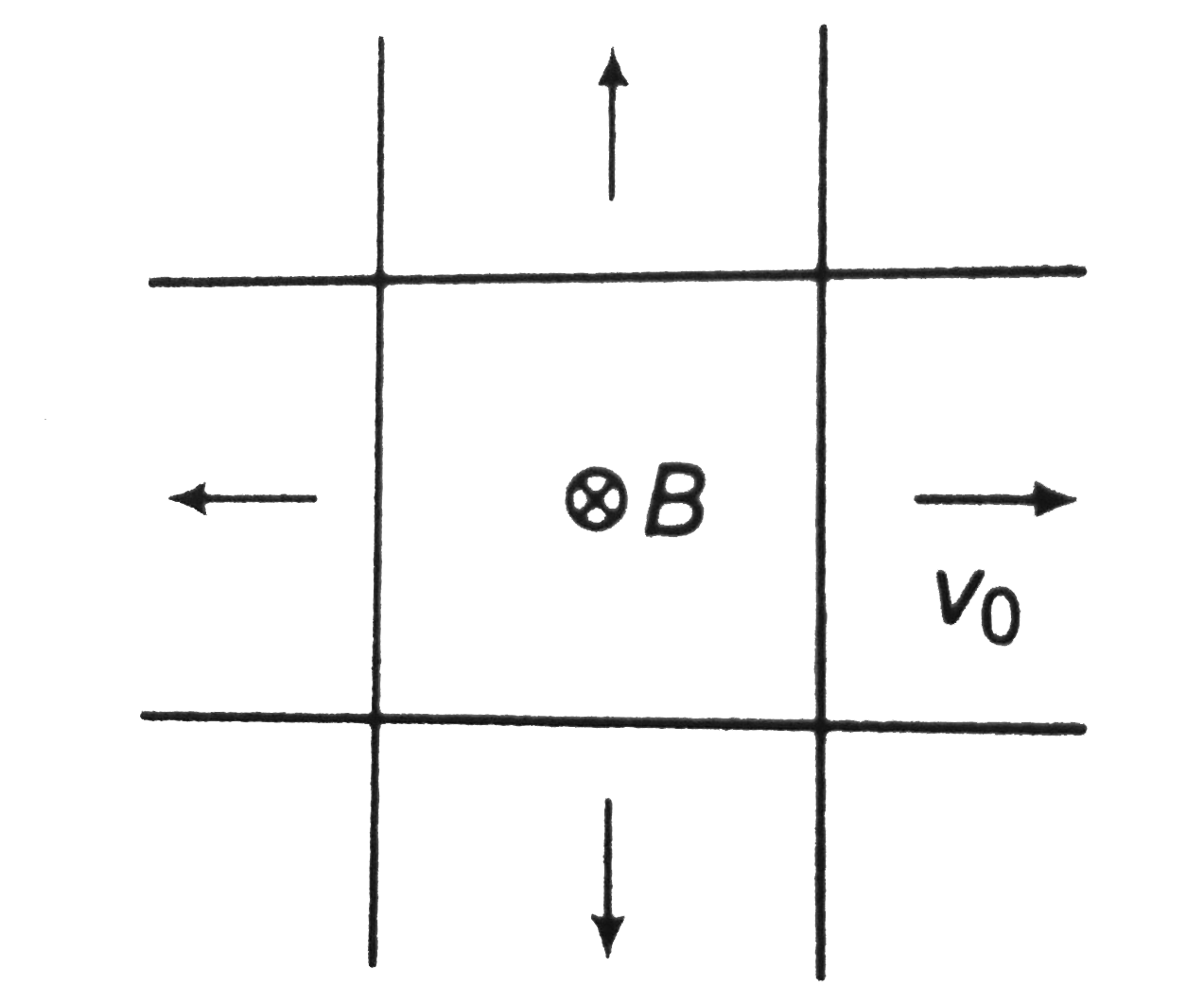 AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ
AaBv0λ(a+v0t)BaBv02λCBv0λDBv02λ
A conductor is moving with velocity v in a region of uniform magnetic field B.The electric field at P inside conductor is
View SolutionA circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is 4ohm. The net magnetic field at the centre of the conductor is

View SolutionA current of 0.2A flows through a conductor of resistance 4.5Ω. Calculate the potential difference at the ends of the conductor.
View SolutionWhat is the resistance of a conductor ? State the factors on which resistance of a conductor depends? How is it related to conductivity of the conductor?
View SolutionThe resistance of two conductors in series is 18Ω and the resistance becomes 4Ω when connected in parallel. Find the resistance of individual conductors.
View SolutionTwo parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward witha constant velocity v0 at t=0. Then, induced current in the loop at any time is (λ is resistance per unit length of the conductors)

View Solution
