One end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
mω2l
zero
mg
12mω2l
The correct Answer is:D
To solve the problem of finding the horizontal component of the force exerted by the clamp on a rotating uniform rod, we can follow these steps:
1. Understand the System:
- We have a uniform rod of mass m and length l that is clamped at one end. The rod rotates about the clamped end with a uniform angular velocity ω.
2. Consider an Element of the Rod:
- Take a small element of the rod at a distance x from the clamped end, with a small length dx.
3. Identify Forces Acting on the Element:
- The tension in the rod at distance x can be denoted as T. At the next segment of the rod, the tension will be T+dT.
4. Centripetal Force Requirement:
- For the small element dx to rotate in a circular path, it requires a centripetal force. This centripetal force is provided by the difference in tension:
FC=T−(T+dT)=−dT
5. Express the Centripetal Force:
- The mass of the small element dm can be expressed as:
dm=mldx
- The centripetal force required for this mass rotating at radius x is given by:
FC=dm⋅ω2⋅x=mldx⋅ω2⋅x
6. Set Up the Equation:
- Equating the expressions for centripetal force:
−dT=ml⋅ω2⋅x⋅dx
- Rearranging gives:
dT=−mω2lxdx
7. Integrate to Find Tension:
- Integrate dT from T (at x) to 0 (at L):
∫0TdT=−∫Lxmω2lxdx
- This results in:
T=mω22l(L2−x2)
8. Find the Tension at the Clamped End:
- To find the tension at the clamped end (where x=0):
T(0)=mω22lL2
9. Conclusion:
- The horizontal component of the force exerted by the clamp on the rod is equal to the tension at the clamped end:
Fhorizontal=T(0)=mω2L2
Final Answer:
The horizontal component of the force exerted by the clamp on the rod is:
Fhorizontal=mω2L2
- We have a uniform rod of mass m and length l that is clamped at one end. The rod rotates about the clamped end with a uniform angular velocity ω.
- Take a small element of the rod at a distance x from the clamped end, with a small length dx.
- The tension in the rod at distance x can be denoted as T. At the next segment of the rod, the tension will be T+dT.
- For the small element dx to rotate in a circular path, it requires a centripetal force. This centripetal force is provided by the difference in tension:
FC=T−(T+dT)=−dT
- The mass of the small element dm can be expressed as:
dm=mldx
- The centripetal force required for this mass rotating at radius x is given by:
FC=dm⋅ω2⋅x=mldx⋅ω2⋅x
- Equating the expressions for centripetal force:
−dT=ml⋅ω2⋅x⋅dx
- Rearranging gives:
dT=−mω2lxdx
- Integrate dT from T (at x) to 0 (at L):
∫0TdT=−∫Lxmω2lxdx
- This results in:
T=mω22l(L2−x2)
- To find the tension at the clamped end (where x=0):
T(0)=mω22lL2
- The horizontal component of the force exerted by the clamp on the rod is equal to the tension at the clamped end:
Fhorizontal=T(0)=mω2L2
The horizontal component of the force exerted by the clamp on the rod is:
Fhorizontal=mω2L2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples29videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionA tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
View Solution
Knowledge Check
- Question 1 - Select One
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. Determine the force exerted by the liquid at the other end.
AMω2L2BMω2LCMω2L4DMω2L22
A uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?
 View Solution
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
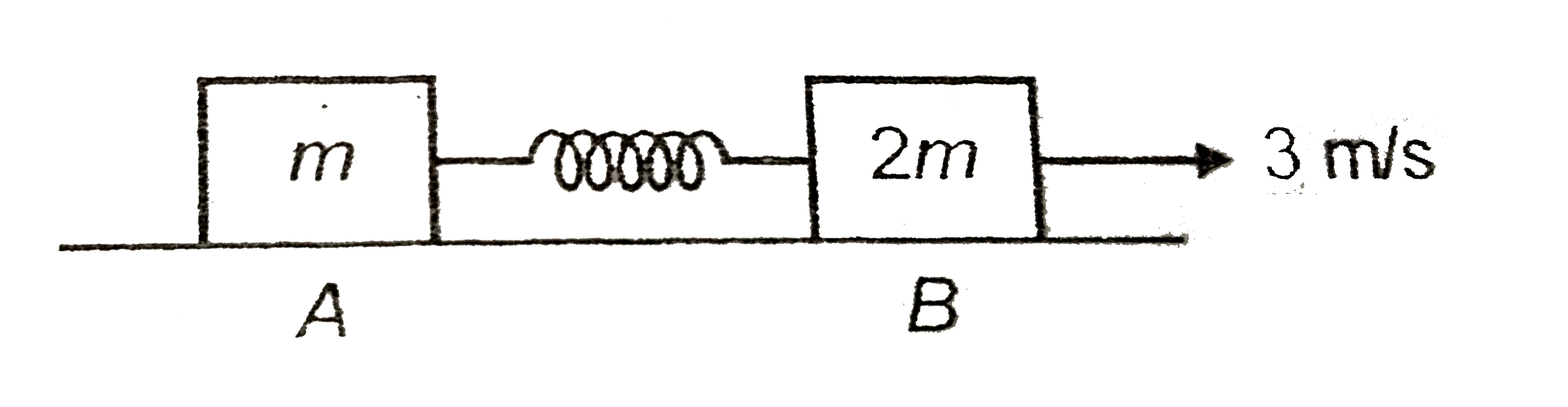 View Solution
View Solution

