One third height of a cubical block of edge 6cm is floating in kerosene oil of specific gravity 0.8. To make the block to be just immersed some water is poured. What is the height of the water column?
To solve the problem, we need to follow these steps:
Step 1: Understand the Problem
We have a cubical block of edge length 6 cm, where one-third of its height is floating in kerosene oil with a specific gravity of 0.8. We need to determine the height of the water column required to make the block just immersed.
Step 2: Calculate the Volume of the Block
The volume V of the cubical block can be calculated using the formula:
V=a3
where a is the edge length of the cube. Given a=6cm:
V=(6cm)3=216cm3
Step 3: Determine the Weight of the Block
The weight W of the block can be expressed as:
W=ρb⋅V⋅g
where ρb is the density of the block and g is the acceleration due to gravity.
Step 4: Calculate the Density of Kerosene
The specific gravity of kerosene is given as 0.8. The density of water ρw is approximately 1000kg/m3. Thus, the density of kerosene ρk is:
ρk=0.8⋅ρw=0.8⋅1000kg/m3=800kg/m3
Step 5: Calculate the Volume of the Block Submerged in Kerosene
Since one-third of the block is floating, the submerged volume Vs in kerosene is:
Vs=13⋅V=13⋅216cm3=72cm3
Step 6: Calculate the Buoyant Force from Kerosene
The buoyant force Fb acting on the block due to the kerosene is given by:
Fb=ρk⋅Vs⋅g
Substituting the values:
Fb=800kg/m3⋅72cm3⋅g
Converting 72cm3 to m3:
Fb=800⋅72×10−6⋅g=0.0576g
Step 7: Set Up the Equilibrium Condition
For the block to be just immersed, the total buoyant force must equal the weight of the block:
Fb+Fw=W
where Fw is the buoyant force due to the water added.
Step 8: Calculate the Buoyant Force from Water
Let the height of the water column be h. The buoyant force from the water is:
Fw=ρw⋅Vw⋅g=ρw⋅(A⋅h)⋅g
where A is the cross-sectional area of the block. Since A=a2:
Fw=1000⋅(6×6)⋅h⋅g=36,000⋅h⋅g
Step 9: Solve for the Height of the Water Column
Setting the total buoyant force equal to the weight of the block:
0.0576g+36,000⋅h⋅g=ρb⋅V⋅g
Substituting ρb as 23⋅ρk:
0.0576+36,000⋅h=23⋅800⋅216
Calculating the right-hand side:
23⋅800⋅216=115200
Now, we can solve for h:
36,000⋅h=115200−0.0576
h=115200−0.057636000
Calculating h:
h≈3.2m
Final Answer
The height of the water column required to make the block just immersed is approximately 3.2 m.
---
We have a cubical block of edge length 6 cm, where one-third of its height is floating in kerosene oil with a specific gravity of 0.8. We need to determine the height of the water column required to make the block just immersed.
The volume V of the cubical block can be calculated using the formula:
V=a3
where a is the edge length of the cube. Given a=6cm:
V=(6cm)3=216cm3
The weight W of the block can be expressed as:
W=ρb⋅V⋅g
where ρb is the density of the block and g is the acceleration due to gravity.
The specific gravity of kerosene is given as 0.8. The density of water ρw is approximately 1000kg/m3. Thus, the density of kerosene ρk is:
ρk=0.8⋅ρw=0.8⋅1000kg/m3=800kg/m3
Since one-third of the block is floating, the submerged volume Vs in kerosene is:
Vs=13⋅V=13⋅216cm3=72cm3
The buoyant force Fb acting on the block due to the kerosene is given by:
Fb=ρk⋅Vs⋅g
Substituting the values:
Fb=800kg/m3⋅72cm3⋅g
Converting 72cm3 to m3:
Fb=800⋅72×10−6⋅g=0.0576g
For the block to be just immersed, the total buoyant force must equal the weight of the block:
Fb+Fw=W
where Fw is the buoyant force due to the water added.
Let the height of the water column be h. The buoyant force from the water is:
Fw=ρw⋅Vw⋅g=ρw⋅(A⋅h)⋅g
where A is the cross-sectional area of the block. Since A=a2:
Fw=1000⋅(6×6)⋅h⋅g=36,000⋅h⋅g
Setting the total buoyant force equal to the weight of the block:
0.0576g+36,000⋅h⋅g=ρb⋅V⋅g
Substituting ρb as 23⋅ρk:
0.0576+36,000⋅h=23⋅800⋅216
Calculating the right-hand side:
23⋅800⋅216=115200
Now, we can solve for h:
36,000⋅h=115200−0.0576
h=115200−0.057636000
Calculating h:
h≈3.2m
The height of the water column required to make the block just immersed is approximately 3.2 m.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Textbook Exercises)
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Additional Exercises)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
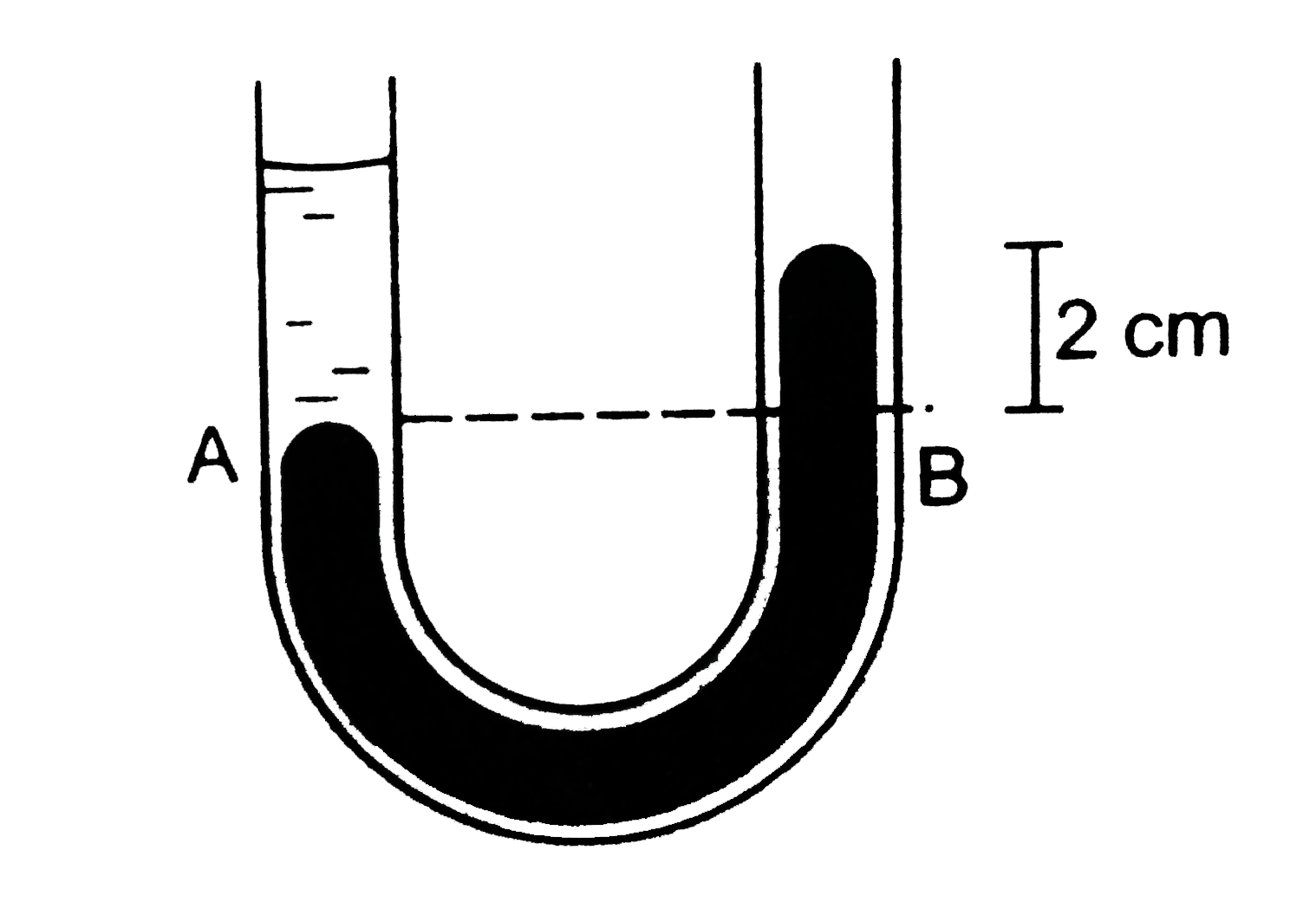 ,
,
View Solution
Knowledge Check
A block weighs 15 N in air and 12 N.when immersed in water. The specific gravity of the block is
A0.8B0.25C5/4D5A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cmWater rises upto 10 cm height in a long capillary tube. If this tube is immersed in water so that the height above the water surface is only 8 cm, then
AWater flows out continously from the upper andBWater rises upto end and forms a spherical surfaceCWater only rises upto 6 c m heightDWater does not rise at all
(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View SolutionA tunning fork having a frequency of 170 Hz is vibrating just above a cylindrical tube. The height of the tube is 110 cm. Water is slowly poured in it. What is the minimum height (in cm) of water column required for resonance to occur? (Velocity of sound in air =340ms−1)
View SolutionA cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View SolutionThere is some water in a cylindrical vessel of diameter 11 cm .If an iron cube of edge 5.5 cm is entrirely immersed in the water what is the rise in the height of the water in the vessel?
View SolutionA U-tube contains water in its lower part. Then 32 cm of kerosene of relative density 0.8 is poured into one limb and a vegetable oil of reative density 0.65 is poured into the other. The water level in the kerosene oil side is 5 cm lower that in the other . what is the height of the column of vegtable oil ?\
View Solution
