Particles of mass 1.6×10−27 kg and charge 1.6×10−19C are accelerated in a cyclotron of dee radius 40cm. It employs a magnetic field 0.4T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
Here mass of charged particle m=1.6×10−27kg, charge q=1.6×10−19C, radius of dee R=40cm=0.4m and magnetic field B = 0.4T.
∴ Kinetic energy of the particle beam imparted by the cyclotron accelerator
Kmax=B2q2R22m=(0.4)2×(1.6×10−19)2×(0.4)22×(1.6×10−27)J
=(0.4)2×(1.6×10−19)2×(0.4)22×(1.6×10−27)×(1.6×10−13)=128MeV
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION C
10 Videos
- ATOMSBOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SELF ASSESSMENT TEST (SECTION C)
2 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
11 Videos
Similar Questions
a) Obtain the expression for the deflecting torque acting on the current carrying rectangular coil of a Galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer? b) Particles of mass 1.6×10−27 kg and charge 1.6×10−19 C are accelerated in a cyclotron of dee radius 40 cm. It employs a magnetic field of 0.4 T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
View SolutionAnswer the following:
a) Obtain the expression for the deflecting torque acting on the current carrying rectangular coil of a Galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?
b) Particles of mass 1.6×10−27 kg and charge 1.6×10−19 C are accelerated in a cyclotron of dee radius 40 cm. It employs a magnetic field of 0.4T. Find the kinetic energy (in MeV) of the particle beam imparted by the accelerator.
View Solution
Knowledge Check
A proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
A1.6×10−15 JB1.6×10−13 JC1.6×10−21 JD3.2×10−13JA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
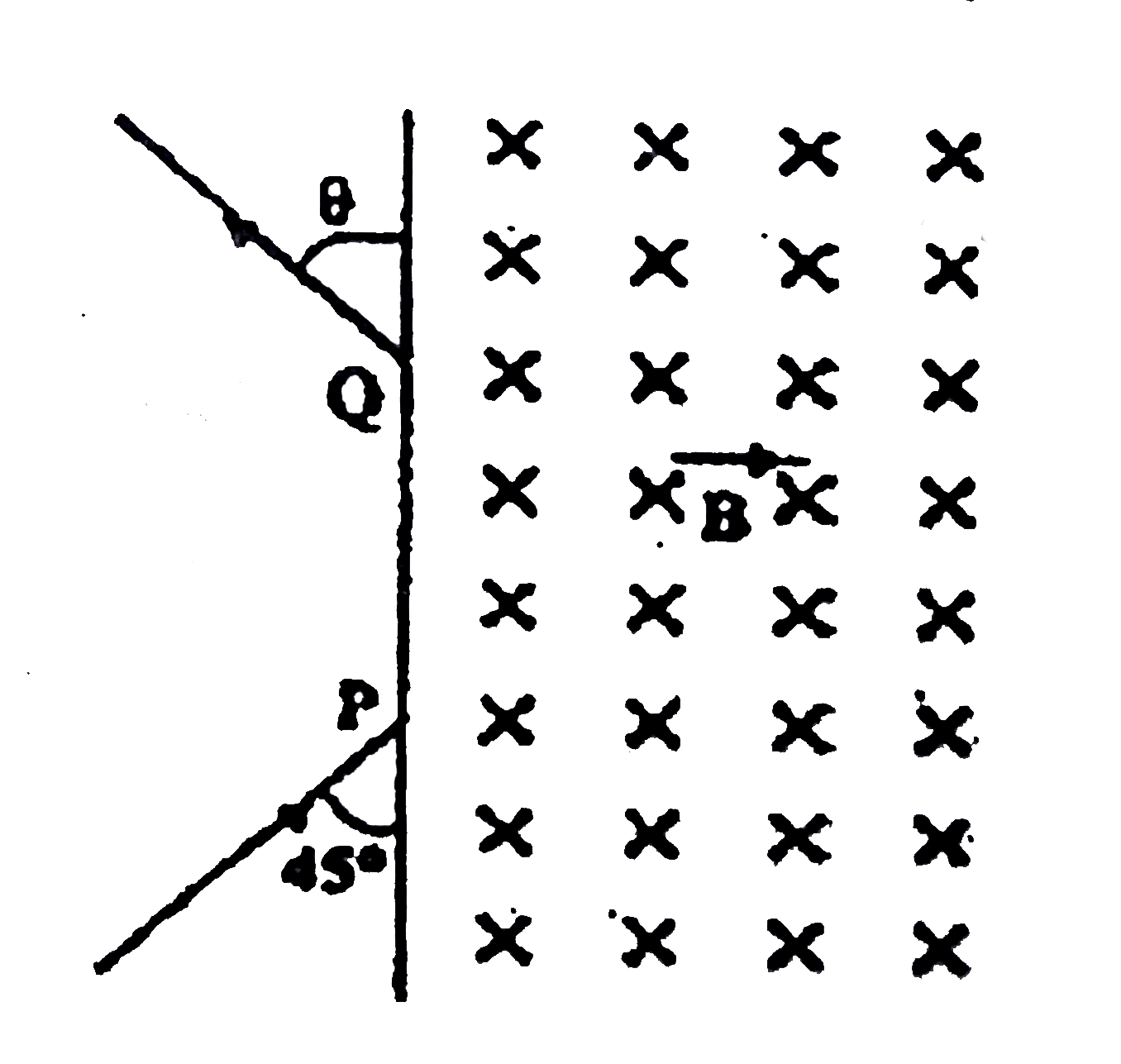 A0.14 mB0.28 mC0.4 mD0.5 m
A0.14 mB0.28 mC0.4 mD0.5 mA particle of mass 'm' and charge 'Q' is acceleration in cyclotron. If magnetic field is 'B' and radius cyclotron is r then find the kinetic energy of particle.
AQBr2mBQ2B2r2mCQ2B2r22mDQ2B2r2m
A proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be

View SolutionA cyclotron oscillator frequency is 10MHz. What should be the operating magnetic field for accelerating α-particle? If the radius of the dees is 50cm, what is the kinetic energy in MeV of the α-particle beam produced by the accelerator?
(e=1⋅6×10−19C,mα=4⋅0028a.m.u.,1a.m.u.=1⋅66×10−27kg)
View SolutionA cyclotron's oscillator frequency is 10MHz. What should be the operating magnetic field fro accelerating protons? If the radius of its dees is 60cm, what is the kinetic energy (in MeV) of the proton beam produced by the acceleration?
(e−1.60×10−19C,mp=1.67×10−27kg,1MeV=1.6×10−13J)
View SolutionA cyclotron's oscillator frequency is 10MHz. What should be the operating magnetic field fro accelerating protons? If the radius of its dees is 60cm, what is the kinetic energy (in MeV) of the proton beam produced by the acceleration?
(e−1.60×10−19C,mp=1.67×10−27kg,1MeV=1.6×10−13J)
View Solution
