Repeat both the parts of the above question, If the train moves with an acceleration a=g/2 up the plane.
To solve the problem step by step, we need to analyze the situation where a train is moving up an inclined plane with an acceleration a=g2. We will consider the forces acting on a box placed on the inclined plane and derive the necessary equations.
Step 1: Understand the Forces Acting on the Box
The box experiences the following forces:
- The gravitational force acting downwards, mg.
- The tension T in the string acting along the incline.
- The normal force N acting perpendicular to the incline.
Step 2: Set Up the Coordinate System
Let’s assume the incline makes an angle θ with the horizontal. The forces can be resolved into components parallel and perpendicular to the incline:
- The component of gravitational force acting down the incline: mgsinθ.
- The component of gravitational force acting perpendicular to the incline: mgcosθ.
Step 3: Apply Newton's Second Law
Since the train is accelerating up the incline with a=g2, we can apply Newton's second law along the incline:
T−mgsinθ=ma
Substituting a=g2:
T−mgsinθ=m(g2)
This can be rearranged to:
T=mgsinθ+mg2
Step 4: Analyze the Forces Perpendicular to the Incline
Now, considering the forces acting perpendicular to the incline, we have:
N=mgcosθ
Since there is no acceleration in the perpendicular direction, the normal force balances the perpendicular component of the weight.
Step 5: Relate Tension and Normal Force
The tension can also be expressed in terms of the angle θ:
Tcosθ=N
Substituting for N:
Tcosθ=mgcosθ
Step 6: Solve for Tension
From the equation T=mgsinθ+mg2, we can substitute T into the equation for the normal force:
(mgsinθ+mg2)cosθ=mgcosθ
This simplifies to:
mgsinθcosθ+mg2cosθ=mgcosθ
Step 7: Rearranging the Equation
Rearranging gives:
mgsinθcosθ=mgcosθ−mg2cosθ
This simplifies to:
mgsinθcosθ=mg2cosθ
Dividing both sides by mgcosθ (assuming cosθ≠0):
sinθ=12
Step 8: Find the Angle θ
The angle θ can be found using the inverse sine function:
θ=sin−1(12)=30∘
Step 9: Calculate Tension
Now substituting θ=30∘ back into the tension equation:
T=mgsin(30∘)+mg2=mg⋅12+mg2=mg
Final Solution
Thus, the tension in the string when the train accelerates up the incline with a=g2 is:
T=mg
The box experiences the following forces:
- The gravitational force acting downwards, mg.
- The tension T in the string acting along the incline.
- The normal force N acting perpendicular to the incline.
Let’s assume the incline makes an angle θ with the horizontal. The forces can be resolved into components parallel and perpendicular to the incline:
- The component of gravitational force acting down the incline: mgsinθ.
- The component of gravitational force acting perpendicular to the incline: mgcosθ.
Since the train is accelerating up the incline with a=g2, we can apply Newton's second law along the incline:
T−mgsinθ=ma
Substituting a=g2:
T−mgsinθ=m(g2)
This can be rearranged to:
T=mgsinθ+mg2
Now, considering the forces acting perpendicular to the incline, we have:
N=mgcosθ
Since there is no acceleration in the perpendicular direction, the normal force balances the perpendicular component of the weight.
The tension can also be expressed in terms of the angle θ:
Tcosθ=N
Substituting for N:
Tcosθ=mgcosθ
From the equation T=mgsinθ+mg2, we can substitute T into the equation for the normal force:
(mgsinθ+mg2)cosθ=mgcosθ
This simplifies to:
mgsinθcosθ+mg2cosθ=mgcosθ
Rearranging gives:
mgsinθcosθ=mgcosθ−mg2cosθ
This simplifies to:
mgsinθcosθ=mg2cosθ
Dividing both sides by mgcosθ (assuming cosθ≠0):
sinθ=12
The angle θ can be found using the inverse sine function:
θ=sin−1(12)=30∘
Now substituting θ=30∘ back into the tension equation:
T=mgsin(30∘)+mg2=mg⋅12+mg2=mg
Thus, the tension in the string when the train accelerates up the incline with a=g2 is:
T=mg
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
In the above question, the acceleration of the rim will be?
View SolutionA plumb bob is hung from the ceiling of a train compartment. If the train moves with an acceleration a along a straight horizontal track, the string supporting the bob makes an angle tan1(ag) with the normal to the ceiling. Suppose the train moves on an inclined straight track with uniform velocity, if the angle of incline is tan−1(ag), the string again makes the same angle with the normal to the ceiling. Can a person sitting inside the compartment tell by looking at the plumb line whether the train is accelerated on a horizontal straight track or it is going on an incline? If yes, how? If no, suggest a method to do so.
View SolutionFor what value of 'a' block slides up the Plane with an acceleration 'g' relative to the inclined plane.
View SolutionIn the above question, if the disc executes rotatory motion, its angular acceleration will be:
View SolutionFor what value of 'a' block slides up the Plane with an acceleration 'g' relative to the inclined plane.
View SolutionA block of mass 2 kg rests on an inclined plane which makes an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is √3/2. (i) What force should be applied on the block so that it moves down without any acceleration ? (ii) What force should be applied on the block so that it moves up without any acceleration ? (iii) Calculate the ratio of the powers in the above two cases if the block moves with uniform speed in both the cases.
View SolutionA train in standing on a platform, a man inside a compartment of a train drops a stone. At the same instant train starts to move with constant acceleration. The path of the particle as seen by the person who drops the stone is:
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
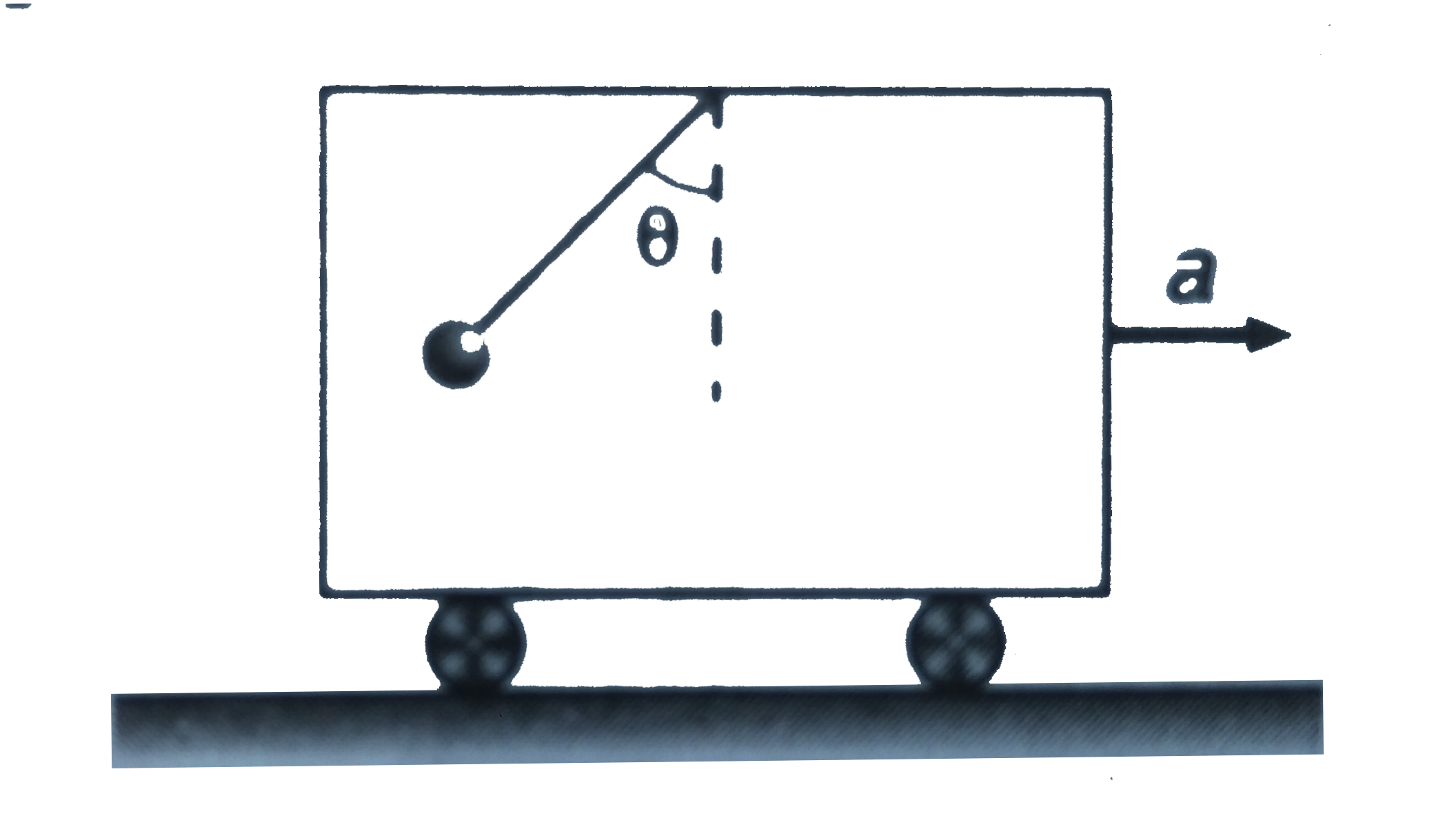
View SolutionWhen an empty lift is moving down with an acceleration of g4ms−2 the tension in the cable is 9000N. When the lift is moving up with an acceleration of g3ms−2 the tension in the cable is
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2
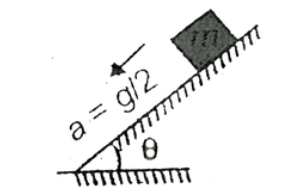
View Solution
