A 2kg object is slide along the frictionless floor with intial transverse volocity (10m/s)ˆk (a) Describe the motion (a) in car's frame and (b) in ground frame.
To solve the problem, we will analyze the motion of the object in two different frames: the car's frame (which is a non-inertial frame) and the ground frame (which is an inertial frame).
1. Identify the Given Information:
- Mass of the object, m=2kg
- Initial transverse velocity in the z-direction, vz=10m/s
- Acceleration of the car (non-inertial frame), a=5m/s2 in the x-direction.
2. Apply Pseudo Force:
- Since the car is accelerating, we need to introduce a pseudo force acting on the object. The pseudo force Fpseudo is given by:
Fpseudo=−m⋅a=−2kg⋅5m/s2=−10N (in the x-direction)
3. Determine the Motion in the x-direction:
- The initial velocity in the x-direction, ux=0.
- The acceleration in the x-direction due to the pseudo force is −5m/s2.
- Using the equation of motion vx=ux+axt:
vx=0−5t=−5t
4. Calculate the Displacement in the x-direction:
- Using the equation sx=uxt+12axt2:
sx=0+12(−5)t2=−2.5t2
5. Determine the Motion in the z-direction:
- The initial velocity in the z-direction, uz=10m/s.
- The acceleration in the z-direction is 0.
- Using the equation of motion:
vz=uz+azt=10+0=10m/s
6. Calculate the Displacement in the z-direction:
- Using the equation sz=uzt+12azt2:
sz=10t+0=10t
Summary of Motion in Car's Frame:
- Velocity in x-direction: vx=−5t
- Displacement in x-direction: sx=−2.5t2
- Velocity in z-direction: vz=10m/s
- Displacement in z-direction: sz=10t
---
Part (b): Motion in the Ground Frame
1. Identify the Given Information:
- In the ground frame, the object is not subjected to any pseudo force as it is an inertial frame.
- The initial velocity in the z-direction remains vz=10m/s.
- The acceleration in the x-direction is 0.
2. Determine the Motion in the x-direction:
- Since there is no acceleration, the velocity in the x-direction remains 0:
vx=0
3. Calculate the Displacement in the x-direction:
- The displacement in the x-direction is also 0:
sx=0
4. Determine the Motion in the z-direction:
- The initial velocity in the z-direction is 10m/s and the acceleration is 0:
vz=10m/s
5. Calculate the Displacement in the z-direction:
- Using the equation:
sz=uzt+12azt2=10t+0=10t
Summary of Motion in Ground Frame:
- Velocity in x-direction: vx=0
- Displacement in x-direction: sx=0
- Velocity in z-direction: vz=10m/s
- Displacement in z-direction: sz=10t
---
- Mass of the object, m=2kg
- Initial transverse velocity in the z-direction, vz=10m/s
- Acceleration of the car (non-inertial frame), a=5m/s2 in the x-direction.
- Since the car is accelerating, we need to introduce a pseudo force acting on the object. The pseudo force Fpseudo is given by:
Fpseudo=−m⋅a=−2kg⋅5m/s2=−10N (in the x-direction)
- The initial velocity in the x-direction, ux=0.
- The acceleration in the x-direction due to the pseudo force is −5m/s2.
- Using the equation of motion vx=ux+axt:
vx=0−5t=−5t
- Using the equation sx=uxt+12axt2:
sx=0+12(−5)t2=−2.5t2
- The initial velocity in the z-direction, uz=10m/s.
- The acceleration in the z-direction is 0.
- Using the equation of motion:
vz=uz+azt=10+0=10m/s
- Using the equation sz=uzt+12azt2:
sz=10t+0=10t
- Velocity in x-direction: vx=−5t
- Displacement in x-direction: sx=−2.5t2
- Velocity in z-direction: vz=10m/s
- Displacement in z-direction: sz=10t
- In the ground frame, the object is not subjected to any pseudo force as it is an inertial frame.
- The initial velocity in the z-direction remains vz=10m/s.
- The acceleration in the x-direction is 0.
- Since there is no acceleration, the velocity in the x-direction remains 0:
vx=0
- The displacement in the x-direction is also 0:
sx=0
- The initial velocity in the z-direction is 10m/s and the acceleration is 0:
vz=10m/s
- Using the equation:
sz=uzt+12azt2=10t+0=10t
- Velocity in x-direction: vx=0
- Displacement in x-direction: sx=0
- Velocity in z-direction: vz=10m/s
- Displacement in z-direction: sz=10t
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question32videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension9videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason28videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
A 2kg object is sliding along the frictionless floor with initial velocity (10m/s)ˆi (a) Describe the motion of the object relation to car (b) when does the object reach its original position relative to the box car.
View SolutionA 2kg object is slide along a rough floor (coefficient of sliding friction =0.3)with initial volocity (10m/s)ˆi. Describe the motion of the object relation to car assuming that the coefficient of static friction is greater than 0.5.
View SolutionAn object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use g=10m/s2.
View SolutionTwo blocks of masses 5kgand2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are respectively :
View SolutionTwo blocks of masses 5kg and 2kg are placed on a frictionless surface and connected by a spring. An external kick gives a velocity of 14m/s to the heavier block in the direction of lighter one. The magnitudes of velocities of two blocks in the centre of mass frame after the kick are, respectively,
View SolutionA particle moves perpendicular towards a plane mirror with a constant speed of 4cm/s.What is the speed of the image observed by an observed moving with 2cm/s along the same direction? Mirror is also moving with a speed of 10cm/s in the opposite direction.
(All speeds are with respect to ground frame of refrence)View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
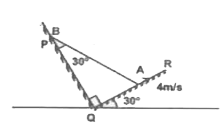 View Solution
View SolutionA 50−kg ball is attached to one end of a 1m cord that has a mass of 0.10kg. The other end o the cord is attached to a ring that can slide on a frictionless horizontal shaft AB, as shown in the diagram.
A horizontal blow is delivered to the cord and excites the fundamental vibratiion with a maximum transverse velocity of 15m/s. Assume that the ball remains essentially stationary as the cord vibrates. [g=9.8m/s2]
 View Solution
View SolutionA 30kg mass is intially at rest on floor of a truck . The coefficient of static friction between the mass and the floor of truck in 0.3 and coefficient of kinetic friction is 0.2 . Intially the truck is travelling due east at constant speed.Find the magnitude and direction of the friction force acting on the mass , if : (take g=10m/s2)
(a) the truck acdceleration at 1.8m/s2 eastward
(b) the truck acdceleration at 3.8m/s2 westwardView SolutionA block of mass 10kg is released on a fixed wedge inside a cart which is moving with constant velocity 10ms1 towards right. There is no relative motion between block and cart. Then work done by mormal reaction on block in two seconds from ground frame will be (g=10 ms^(1))
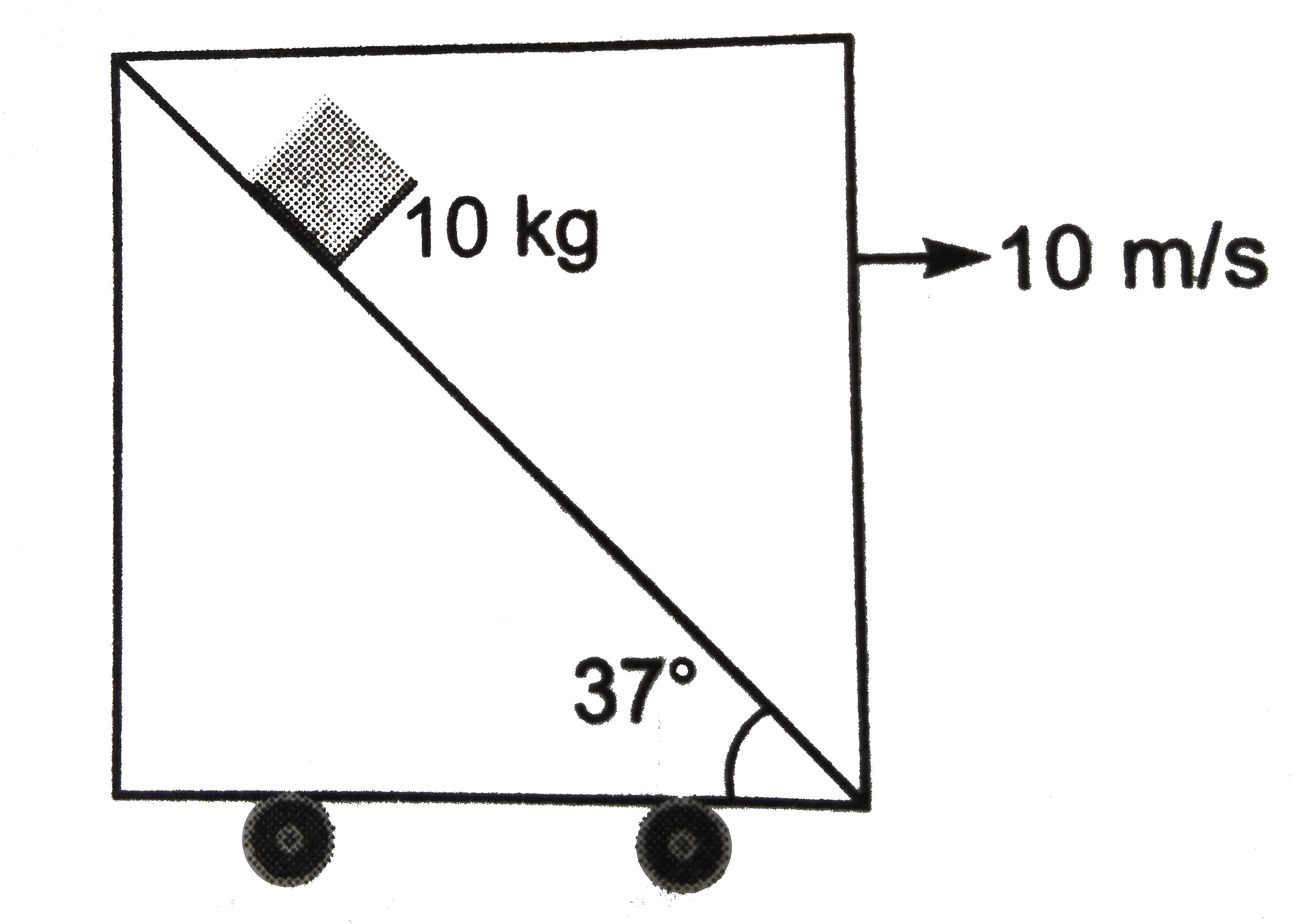 View Solution
View Solution

