State Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.Solution in Punjabi
Ampere.s Circuital Law : This law states that line integral of magnetic field over a closed circuital is equal to μ0 (absolute permeability of free space) times the current threading the circuit.
∮→B.→dl=μ0I
Proof: Consider a long straight conductor PQ carrying current I. Magnetic field lines are produced around the long straight current carrying conductor PQ as concentric circles.
Magnetic field due to infinitely long straight conductor at distance a=B=μ04π2Ia ...(1)
Consider a circle of radius .a. around the current carrying infinitely long straight conductor. Let XY be a small elementary portion of length dl.
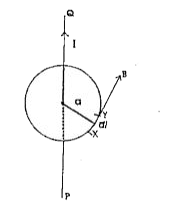
∵→B acts along the tangent to the circle.
∴→B and →dl are in same direction i.e., angle between them is 0∘.
∴∮→B.→dl=∮Bdlcosϕ
=∮Bdlcos0∘
=∮μ04π2Iadl(1) [Using eqn. (1)]
=μ04π2Ia∮dl
=μ04π2Ia(l)
where l=2πa = Length of the circular loop. =
⇒∮→B.→dl=μ04π2Ia(2πa)
⇒∮→B.→dl=μ0I
which is Ampere.s circuital law.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - NUMERICALS PROBLEMS3videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - SHORT ANSWER TYPE QUESTIONS4videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC DIPOLES AND EARTH'S MAGNETISMEXERCISE - Most Expected Questions8videos
MAGNETIC DIPOLES AND EARTH'S MAGNETISM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - NUCLEAR REACTIONSEXERCISE - Numerical Problems9videos
NUCLEAR REACTIONS
Similar Questions
A current of 15A flows through a coil Magnetic field at centre of semi-circular loop of 5.0 cm radius as shown in fig. Find out the direction and magnitude of magnetic field at the centre of the arc.
 02:54View Solution
02:54View SolutionExplain Biot-Savart law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
11:49View SolutionWhat do you mean by Neutral Point in a magnetic field?
05:24View SolutionIt is given that each fission of a chain reaction produces 200 MeV energy. What is the number of fissions taking place per second it the reactor produces 1012W Power ?
03:30View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
05:24View SolutionState Ampere's circuital law. Use this law to find the magnetic field due to a straight infinite current carrying wire. How are the magnetic fields lines different from the electrostatic field lines ?
03:02View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
05:24View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
05:57View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
05:24View SolutionExplain how the expression for magnetic field due to, straight conductor derived from Biot Savart's law is in accordance with Ampere's circuital law.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
05:57View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
02:51View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
02:03View SolutionState Biot-Savart.s law. Derive an expression for magnetic field at a point near an infinitely long and straight current carrying conductor.
02:51View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
02:51View SolutionUsing Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
02:22View Solution

