Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole →p in an electrostatic field →E and (ii) magnetic dipole →M in a magnetic field →B. Write down a set of conditions on →E, →B, →p, →M so that the two motions are verified to be identical. (Assume identical initial conditions).
To verify the analogy between electrostatic and magnetostatic forces acting on electric and magnetic dipoles, we need to establish a set of conditions on the electric field →E, magnetic field →B, electric dipole moment →p, and magnetic dipole moment →M. Below is a step-by-step solution to derive these conditions.
1. Understanding the Torque on Dipoles:
- For an electric dipole →p in an electric field →E, the torque →τE is given by:
→τE=→p×→E
- For a magnetic dipole →M in a magnetic field →B, the torque →τB is given by:
→τB=→M×→B
2. Equating the Torques:
- To verify the analogy, we want the torques to be equal:
→p×→E=→M×→B
3. Considering the Magnitudes:
- The magnitudes of the torques can be expressed as:
|→τE|=pEsinθ
|→τB|=MBsinϕ
- Here, θ is the angle between →p and →E, and ϕ is the angle between →M and →B.
4. Setting Conditions for Identical Motions:
- For the two motions to be identical, we need:
pEsinθ=MBsinϕ
- If we assume that the angles θ and ϕ are equal (i.e., θ=ϕ), we can simplify this to:
pE=MB
5. Relating Electric and Magnetic Fields:
- From electromagnetic theory, we know the relationship between electric and magnetic fields in a vacuum is given by:
E=cB
- Here, c is the speed of light in vacuum.
6. Substituting the Relationship:
- Substitute E=cB into the equation pE=MB:
p(cB)=MB
- Dividing both sides by B (assuming B≠0):
pc=M
7. Final Condition:
- Rearranging gives us the condition:
pM=1c
Summary of Conditions:
- The conditions for the electric field →E, magnetic field →B, electric dipole moment →p, and magnetic dipole moment →M to verify the analogy are:
1. pE=MB
2. E=cB
3. pM=1c
- For an electric dipole →p in an electric field →E, the torque →τE is given by:
→τE=→p×→E
- For a magnetic dipole →M in a magnetic field →B, the torque →τB is given by:
→τB=→M×→B
- To verify the analogy, we want the torques to be equal:
→p×→E=→M×→B
- The magnitudes of the torques can be expressed as:
|→τE|=pEsinθ
|→τB|=MBsinϕ
- Here, θ is the angle between →p and →E, and ϕ is the angle between →M and →B.
- For the two motions to be identical, we need:
pEsinθ=MBsinϕ
- If we assume that the angles θ and ϕ are equal (i.e., θ=ϕ), we can simplify this to:
pE=MB
- From electromagnetic theory, we know the relationship between electric and magnetic fields in a vacuum is given by:
E=cB
- Here, c is the speed of light in vacuum.
- Substitute E=cB into the equation pE=MB:
p(cB)=MB
- Dividing both sides by B (assuming B≠0):
pc=M
- Rearranging gives us the condition:
pM=1c
- The conditions for the electric field →E, magnetic field →B, electric dipole moment →p, and magnetic dipole moment →M to verify the analogy are:
1. pE=MB
2. E=cB
3. pM=1c
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Long Answer Type Questions7videos
MOVING CHARNGES AND MAGNETISM
Similar Questions
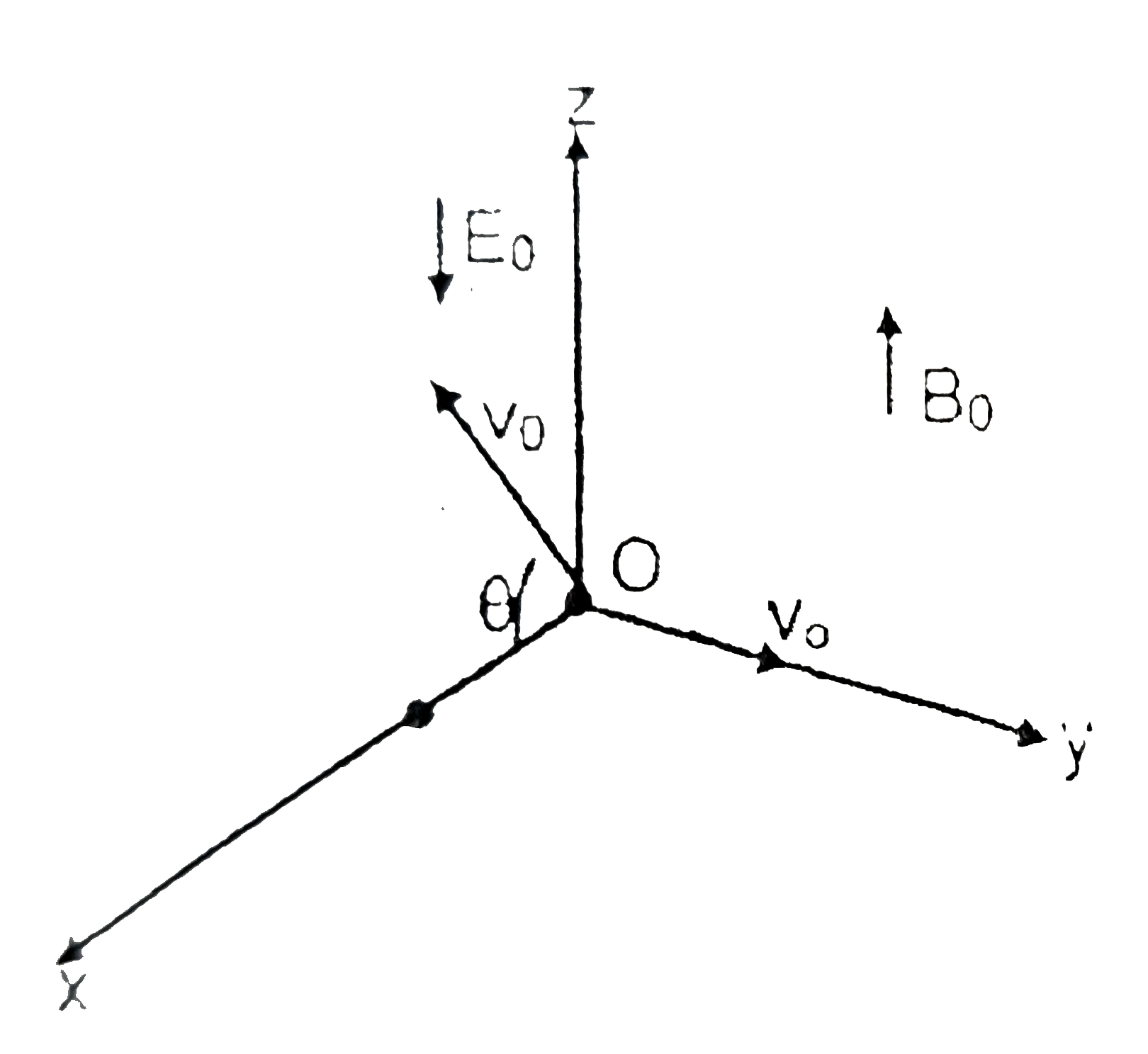
A charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
 View Solution
View SolutionAn electric dipole of dipole moment →p is placed in a uniform electric field →E with its axis inclined to the field. Write an expression for the torque →τ experienced by the dipole in vector form. Show diagrammatically how the dipole should be kept in the electric field so that the torque acting on it is:
(i) maximum (ii) zeroView Solution(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
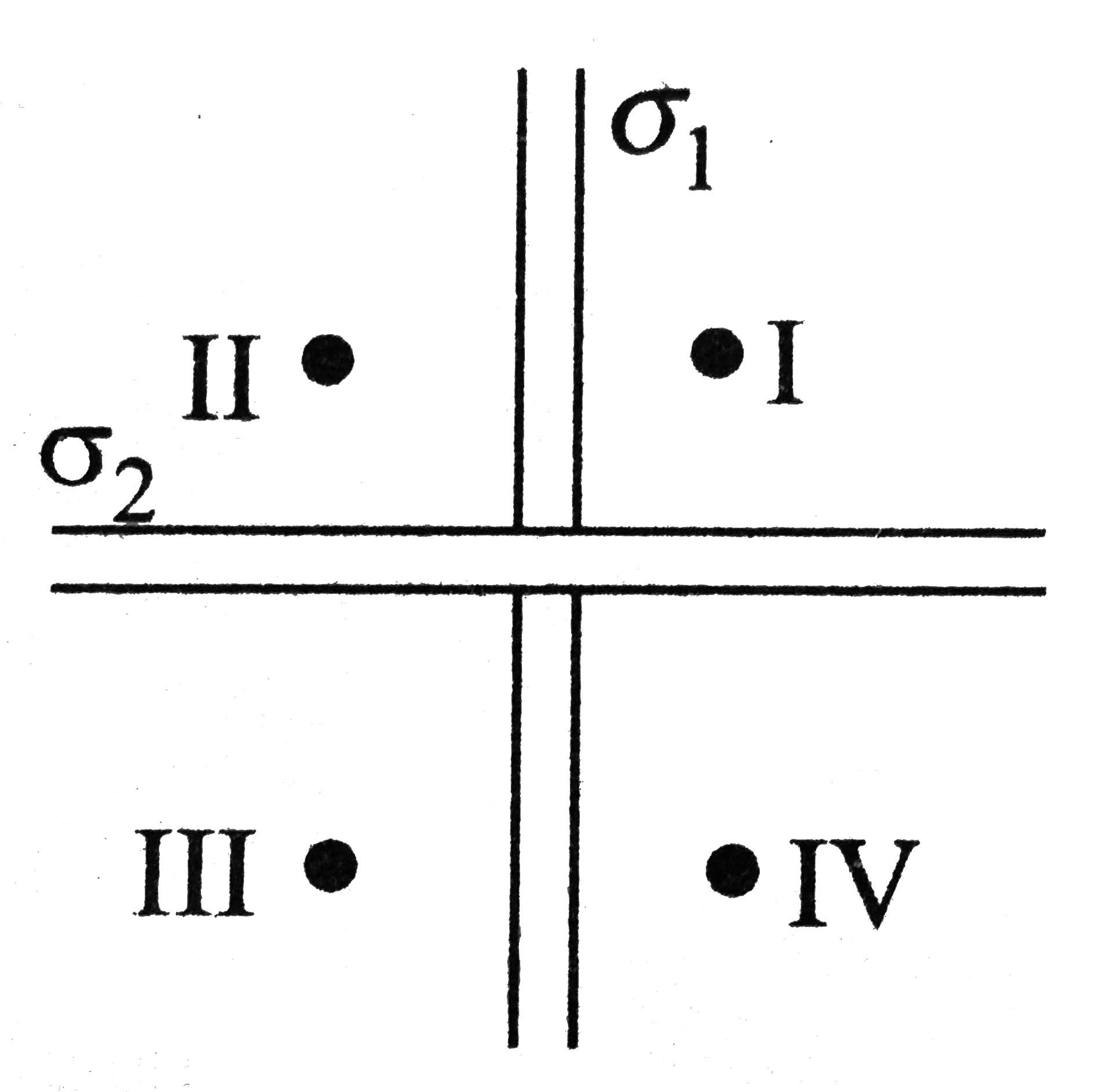
→τ=→m×→B, where →m is the magnetic moment of the loop.View SolutionTwo infinite sheets having charge densities σ1 and σ2 are placed in two perpendicular planes whose two-dimensional view is shown in figure. The charges are distributed uniformly on the sheets in electrostatic equilibrium condition. Four points are marked I, II, III and IV. The electric field intensities at these points are →E1,→E2,→E3,and→E4, respectively. The correct expression for the electric field intensities is
 View Solution
View SolutionConsider two concentric conducting spheres. The outer sphere is hollow and initially has a charge −7Q on it. The inner sphere is solid and has a charge +2Q on it.
a. How much charge is on the outer surface and inner surface of the outer sphere.
b. If a wire is connected between the inner and outer sphere, after electrostatic equilibrium is established how much total charge is on the outer sphere? How much charge is on the outer surface and inner surface of the outer sphere? Does the electric field at the surface of the inside sphere change when the wire is connected?
c. We return to original condition in (a). We now connect the outer sphere to ground with a wire and then disconnect it. How much total charge will be on the outer sphere? How much charge will be on the inner surface and outer surface of the outer sphere?View SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The force between point charge +q and earthed conducting plane isView SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The work done in carrying charge q from distance d to distance y from earthed conducting plane isView SolutionA person wants to roll a solid non-conducting spherical ball of mass m and radius r on a surface whose coefficient of static friction is μ. He placed the ball on the surface wrapped with n turns of closely packed conducting coils of negligible mass at the diameter.
By some arrangement he is able to pass a current i through the coils in anti-clockwise direction when viewed downwards from point P. A constant horizontal magnetic field →B is present throughout the space along the positive x direction as shown in the figure. (Assume μ is large enough to help pure rolling motion and initially the plane of the coils is perpendicular to the y-axs)
If current i is passed through the coil thenView SolutionA person wants to roll a solid non-conducting spherical ball of mass m and radius r on a surface whose coefficient of static friction is μ. He placed the ball on the surface wrapped with n turns of closely packed conducting coils of negligible mass at the diameter.
By some arrangement he is able to pass a current i through the coils in anti-clockwise direction when viewed downwards from point P. A constant horizontal magnetic field →B is present throughout the space along the positive x direction as shown in the figure. (Assume μ is large enough to help pure rolling motion and initially the plane of the coils is perpendicular to the y-axs)
The angular velocity of the ball when it is has rotated through an angle θ is (θ<180∘)View Solution

