The angular velocity , ω of a rotating body or shaft can be measured by attaching an open cylinder of liquid , as shown in Fig and measuring the change in the fluid level , H−h0 , caused by the rotation of the fluid . Determine the relationship between this change in fluid level and the angular velocity . Assume no fluid is spilling out of the vessel.
The height h , of the free surface above the tank bottom can be determined as follows
h−ω2r22g+h0
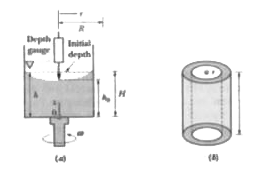
The initial volume of fluid in the tank , Vi=πR2H
The volume of the fluid with the rotating tank can be found by considering a differential element of cylindrical shape as shown in Fig . This cylindrical shell is taken at some arbitary radius , r and thickness dr . Thus , its volume is
dV=2πrhdr
The total volume is , therefore ,
V.=2π∫R0r(ω2r22g+h0)dr=πω2R44g+πR2h0
Since the volume of the fluid in the tank must remain constant (given that none spills over the top) , it follows that πR2H=πω2R44g=πR2h0
or H−h0=ω2R24g
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.151videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.161videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - SAMPLE PROBLEM 14.131videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
ELECTROMAGNETIC WAVES
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
FORCE AND MOTION - I
Similar Questions
A hemispherical bowl of radius R=0.1m is rotating about its own axis (which is verticle) with an angular velocity ω. A particle of mass 10−2kg on the smooth inner surface of the bowl is also rotating with the same ω. The particle is at a height h from the bottom of the bowl (a) obtain the relation betweemn h and ω. what is the minimum value of ω needed, in order to have a non-zero value of h? (b) it is desired to measure g using this set up, by measuring h accurately. assuming that R and Ω are known precisely and least count in the measurement of h is 10−4m, what is the minimum possible error Δg in the measured value of g? (g=10m/s2)
View SolutionA simple accelerometer (an instrument for measuring acceleration) can be made in the form of a tube filled with a liquid and bent as shown. During motion, the level of the liquid in the left arm will be at a height h1 and in the right arm at a height h2. Determine the acceleration a of a carriage in which the accelerometer is installed, assuming that the diameter of the tube is much smaller than h1 and h2.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A simple accelerometer (an instrument for measuring acceleration) can be made in the form of a tube filled with a liquid and bent as shown. During motion, the level of the liquid in the left arm will be at a height h1 and in the right arm at a height h2. Determine the acceleration a of a carriage in which the accelerometer is installed, assuming that the diameter of the tube is much smaller than h1 and h2.
 Ag(h2+h1)h2−h1Bg(h2h1)h2+h1Cg(h2−h1)h2+h1Dg(h2h1)h2−h1
Ag(h2+h1)h2−h1Bg(h2h1)h2+h1Cg(h2−h1)h2+h1Dg(h2h1)h2−h1 - Question 2 - Select One or More
A unifom cylinder of steel of mass M radius R is placed on frictionless bearings and sct to rotate about its axis with angular velocity ω0 After the cylinder has reached the specified state of rotation, it is heated from temperature T0→(T0+ΔT) without any mechanical contact. If (DeltaI)/I is the fractional change in moment of inertia of the cylinder and Δωω0 be the fractional change in the angular velocity of the cylinder and alpha be the coefficient of linear expansion, then
AΔII=2ΔRRBΔII=2Δωω0CΔωω0=−2αΔTDΔII=−2ΔRR
A U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
View SolutionA U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
View SolutionTwo cylinders having radiii R1 and R2 and rotational inertia I1 and I2 respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocityω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity ω2 of the small cylinder in terms of I1,I2,R1,R2 and ω0. (b) Is total angular momentum conserved in this case ?
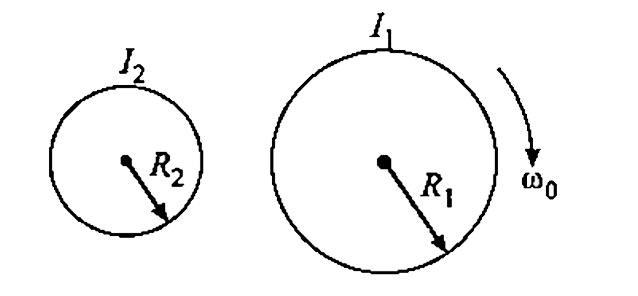 View Solution
View SolutionA horizontally oriented bent thin tube ABC of length 1.4m rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A as shown in figure. The portion BC of tube is parallel to OO' and its length is equal 0.4m. At t=0, AB part of tube is filled with an ideal fluid. The end A of tube is open, the closed end C has a very small orifice. Find the maximum height reached by fluid relative to end C. (take g=10/s2 and ω=10rad/s)
 View Solution
View SolutionA bullet of mass m moving with velocity v strikes and becomes embedded at the edge of a cylinder of mass M and radius R0 as shown in fig. The cylinder, initially at rest, begins to rotate about its symmetry axis, which remains fixed in position. Assuming no frictional torque, what is the angular velocity of the cylinder after this collision? Kinetic energy conseved?
 View Solution
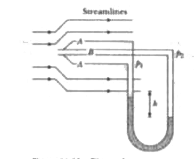
View SolutionFigure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density ρ the density of the fluid in manometer (U-tube) σ and the height h .
 View Solution
View Solution

