The bob of a pendulum at rest is given a sharp hit to impat a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with teh upward vertical.
The correct Answer is:A, B, C
a.Let the velocity at B be v2
12mv21=12mv22+mgl
→12m(10gl)=12mv22+mgl
v22=8gl
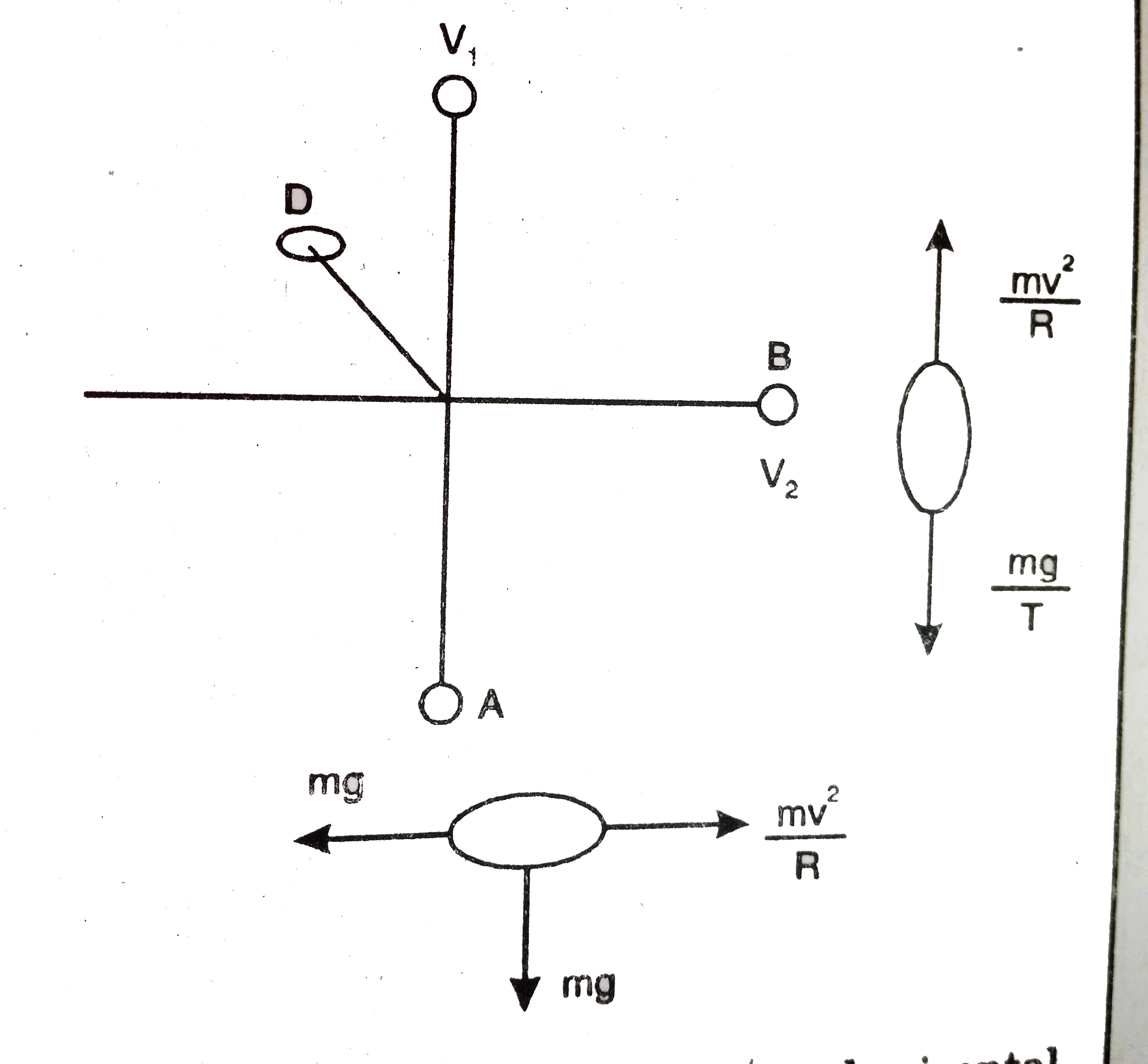
so the tension in the string at horizontal position
T=mv2R=m8gll
=8mg
b. Let the velocity at C be v3
12mv21=12mv23+mg2l
→12m10gl=12mv23+2mgl
→v23=6gl
So, the tension in the string is given by
TC=mv23l−mg=5mg
c. Let the velocity at point D be v4<br>Aga∈1/2 mv_1^2=1/2 mv_4^2+mgl(1+cos60^0)<br>rarr v_4^2=7gl<br>so,thetension∈thestr∈gis<br>T_D=(mv^2)/l-mgcos 60^0<br>=m(7gl)/l-0.5 mg<br>=7mg=0.5mg<br>6.5 mg
Topper's Solved these Questions
Similar Questions
The bobo of a pendulum at rest is given a sharp hit to impart a horizontal velocity u where l is the length of the pendulum. Find the angle rotated by the string before it becomes slack.
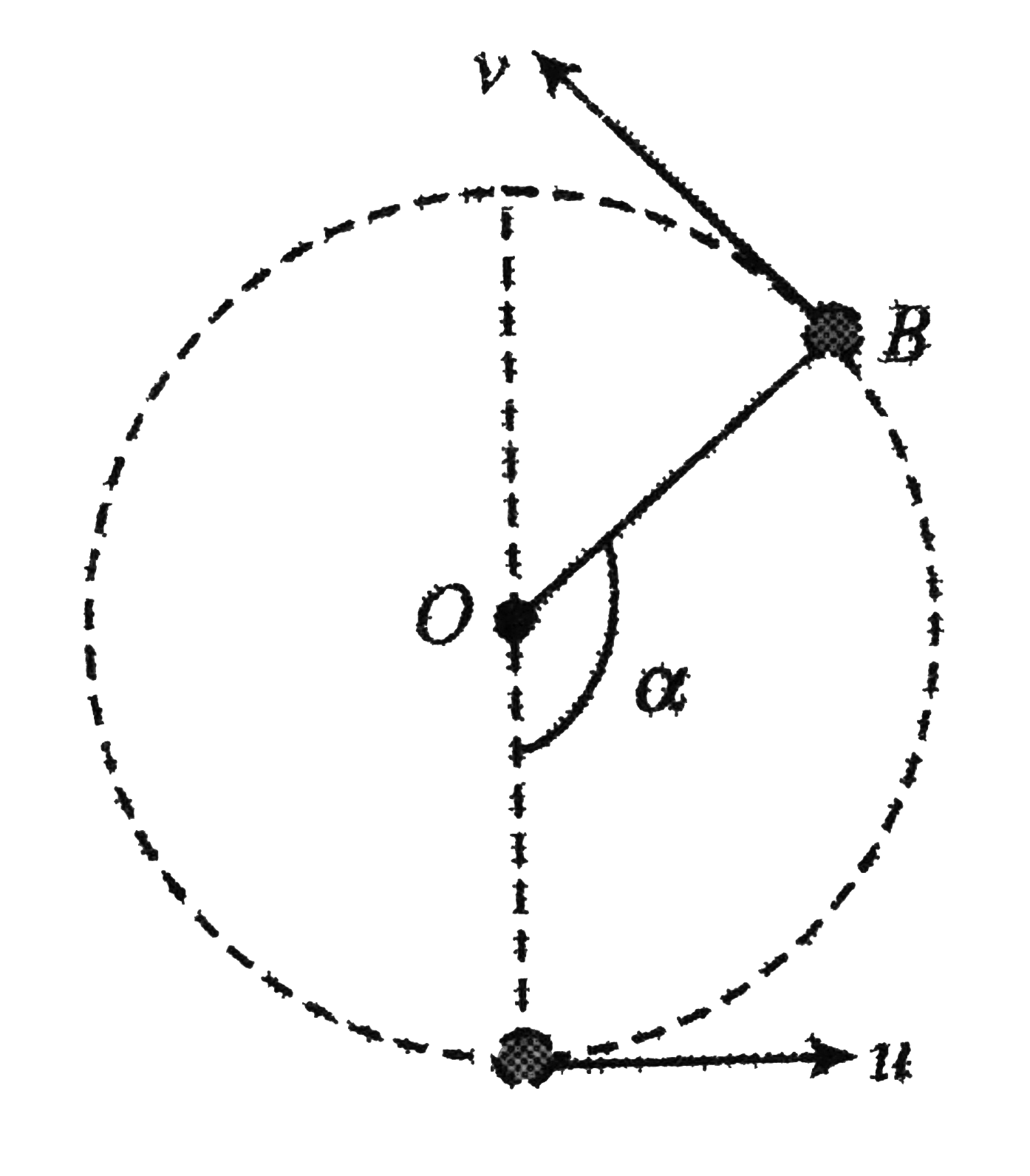
View SolutionThe bob of a stationary pendulum is given a sharp hit to impart it a horizontal speed of √3gl. Find the angle rotated by the string before it becomes slack.
View Solution
Knowledge Check
A particle of mass m is attached to a string of length L and given velocity √10hL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (a) (i) lowest position (ii) highest position, (b) when the string makes an angle 60∘ with (i) lower vertical and (ii) upper vertical.
A11mg , 5 mg , 9.5mg , 6.5 mgB10mg , 5 mg , 9.5mg , 6.5 mgC11mg , 5 mg , 9mg , 6.5 mgD11mg , 5 mg , 9.5mg , 6 mgIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
Aθ=cos−1(1/3)Bθ=60∘Cθ=cos−1(2/3)Dθ=0
The bob of pendulum is project with horizontal velocity of √3gf I is the length of string. Find the angular displacement of string before it becomes slack.

View SolutionThe bob of a simple pendulum of length l is given a sharp hit to impart it a horizontal speed of √3gl . When it was at its lowermost position. Find
angle α shown of the string from upside of vertical and speed of the particle when the string becomes slack.
View SolutionThe bob of a simple pendulum of length 1m hangs at rest. It is suddenly projected horizontally with velocity 10ms−1. Calculate the velocity of the bob and tension of the string when it is horizontal. The mass of the bob is 12kg.
[Hint : See worked out example 4]
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionBob of the simple pendulum is at rest at its lowest position , Sharp hit imparts a speed of √9gl to the pendium bob. Calculate tension of the thread when it makes an angle 60∘ with the vertical .
View SolutionThe bob of a simple pendulum is given a sharp hit impart it a horizontal speed of √3gL. Find an angle made by the string with the upper verticle before it becomes slack. Also, calculate the maximum height attained by the bob above the point of suspension. L is length of the string.
View Solution
