The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
The correct Answer is:A, B
To find the tension in the string of the pendulum at the lowest point, we can follow these steps:
Step 1: Identify the forces acting on the bob
At the lowest point of the pendulum's swing, two forces act on the bob:
1. The gravitational force (weight) acting downward, Fg=mg
2. The tension in the string, T, acting upward.
Step 2: Calculate the gravitational force
Given:
- Mass of the bob, m=100g=0.1kg (since 1 g = 0.001 kg)
- Acceleration due to gravity, g=10m/s2
The gravitational force can be calculated as:
Fg=mg=0.1kg×10m/s2=1N
Step 3: Calculate the centripetal force
At the lowest point, the bob is also undergoing circular motion. The centripetal force required to keep the bob moving in a circle is provided by the tension in the string minus the gravitational force:
Fc=mv2r
where:
- v=1.4m/s (the speed of the bob)
- r=1m (the length of the pendulum)
Calculating the centripetal force:
Fc=mv2r=0.1kg×(1.4m/s)21m=0.1×1.961=0.196N
Step 4: Write the equation for tension
At the lowest point, the tension in the string can be expressed as:
T=Fg+Fc
Substituting the values we calculated:
T=1N+0.196N=1.196N
Step 5: Round the answer
The tension in the string at the lowest point is approximately:
T≈1.2N
Final Answer
The tension in the string at this instant is approximately 1.2 N.
---
At the lowest point of the pendulum's swing, two forces act on the bob:
1. The gravitational force (weight) acting downward, Fg=mg
2. The tension in the string, T, acting upward.
Given:
- Mass of the bob, m=100g=0.1kg (since 1 g = 0.001 kg)
- Acceleration due to gravity, g=10m/s2
Fg=mg=0.1kg×10m/s2=1N
At the lowest point, the bob is also undergoing circular motion. The centripetal force required to keep the bob moving in a circle is provided by the tension in the string minus the gravitational force:
Fc=mv2r
where:
- v=1.4m/s (the speed of the bob)
- r=1m (the length of the pendulum)
Fc=mv2r=0.1kg×(1.4m/s)21m=0.1×1.961=0.196N
At the lowest point, the tension in the string can be expressed as:
T=Fg+Fc
Substituting the values we calculated:
T=1N+0.196N=1.196N
The tension in the string at the lowest point is approximately:
T≈1.2N
The tension in the string at this instant is approximately 1.2 N.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 2
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
A simple pendulm has a length L and a bob of mass M. The bob is vibrating with amplitude a .What is the maximum tension in the string?
View SolutionA pendulum bob can swing along a ciircular path on a smooth inclined plane, as shown in Fig. 3E.31, where m=1.2kg,1=.075m,θ=37∘. At the lowest point of the circle the tension in the sting is T=110N. Determine
(a) the speed of the bob at the lowest point,
(b) the speed of the bob at the highest point on the circle and
(c) the tension in the string at the highest position
(a)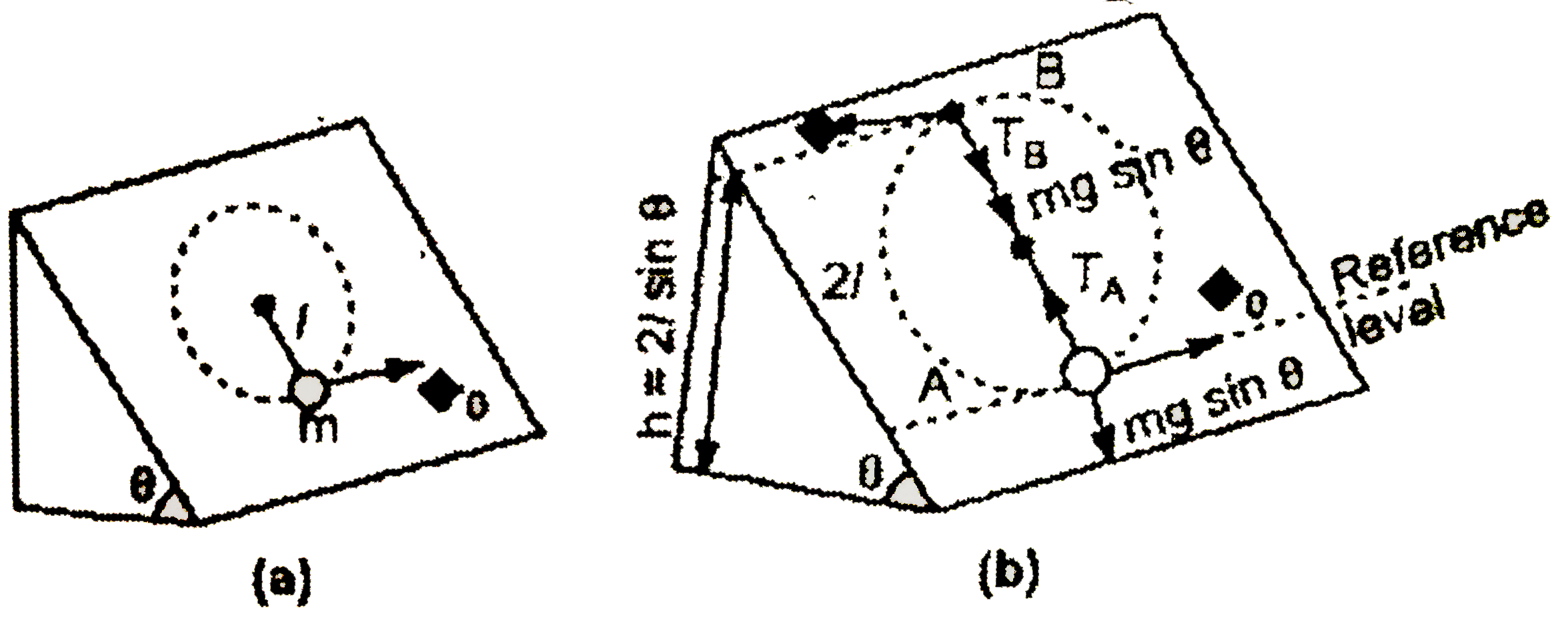
View Solution
Knowledge Check
A body of mass 100 gram is tied at the end of a string of length 1m. It is rotated in a vertical circle at a critical speed of 4 m/s at the highest point . The tension in the string at the huighest point in its path is [ take g=10m/s2]
A0.3NB0.6NC0.9ND1.2NThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
AmgB2 mgC3 mgD6 mgThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
AmgB3 mgC2 mgD6 mg
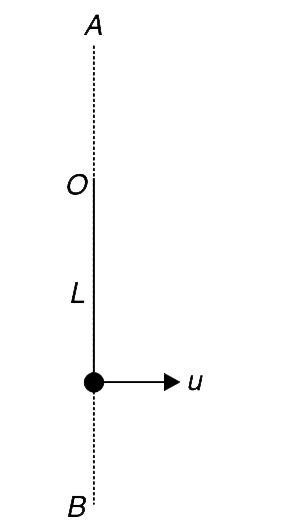
Bob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionThe wooden bob of a simple Pendulum of length 1 m is struck by a bullet of mass 10−3 kg moving with a speed of 300 m s−1 . If the bullet gets embedded into the bob then calculate the height to which the bob will rise before going back to mean position. The mass of bob is 0.8 kg .
View SolutionMass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
View Solutiona simple pendulum with a bob of mass m savings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the strings is-
View Solution
