The coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
The path of the particle is an ellipse
The velocity and acceleration of the particles are normal to each toerh at t=π/2p.
The acceleration of the particle is always directed towards a forucs
The distance travelled by the particle in time interval t=0 to t=π/2p is a.
The correct Answer is:a,b
x=αcos(pt):y=bsin(pt)
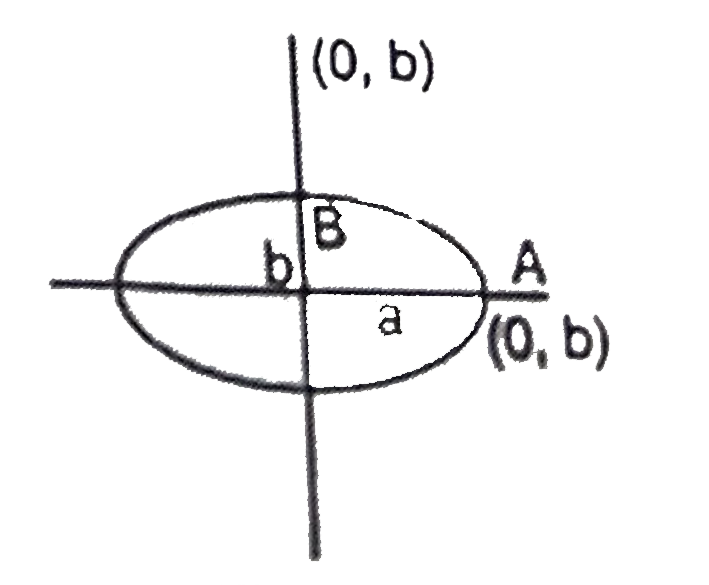
Equation of path in x-y plane is
(xa)2+(yb)2=
i.e., the path of the particle is an elipse.
Position vector of a point P is
→r=acosptˆi+bsinptˆj
⇒→v=P(−asinptˆi+bcosptˆj)
and →a=−p2(−acosptˆi+bsinptˆj)=−p2→r
Acceleration of directed towards the centre.
Also, →v,→a=0 at t=π/2p
At t=0,→r=aˆi
At t=π/2p,→r=bˆj
So, in time t=0 to t=π/2p, particle goes from A to B travelling a distance more than a.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The coordinates of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a)andp are positive constants of appropriate dimensions. Then
Athe path of the particle is an ellipse.Bthe velocity and acceleration of the particle are normal to each other at t=π/(2p).Cthe acceleration of the particle is always directed toward a focus.Dthe distance traveled by the particle in time interval t = 0 to t=π/(2p) is a.The coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
A2t(c-b)B√(c2+b2)C2t√(c2+b2)D2t√(c2+b2)The coordinates of a moving particle at any time t are given by x=ct and y=bt2. The speed of the particle is given by
A2t√b2−c2B√4b2t2+c2C2t(b+c)D2t(b−c)
The coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
View SolutionThe coordinates of a particle moving in XY-plane vary with time as x=4t2,y=2t. The locus of the particle is a : -
View SolutionThe coordinates of a moving particle at any time t are given by x=αt3 and y=βt3. The speed of the particle at time t is given by
View SolutionThe coordinates of a moving particle at time t are given by x=ct2 and y=bt2. The speed of the particle is given by :-
View SolutionThe equations of motion of a particle P(x,y) on a plane are given by x=4+r.cost,y=6+r.sint, where t is time and r is constant . Its velocity at time t is
View Solution
