The friction coeficient bettween the board and the floor shownin filgure is μ. Find the maximum force that the man can exert on the rope so tht the board does not slipon the floor.

Let the minimum force exerted by the man is T
From the free body diagram, <br>R+T=Mg<br>rarr R=Mg-T.i<br>Aga∈R−R−mg−0
R1=R+mg..ii
andT−μR1=0
From equatioon ii, T−μ(r+mg)=0
→T−μR−μmg=0
→T−μ(Mg−T)−μmg=0
T−μMg+μt−μmg=0


T(1+μ)=μMg+μmg
→T=μ(M+m)g1+μ
Maximum force exerted by man is μ(M+m)g1+μ
Topper's Solved these Questions
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Objective -2
5 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
Similar Questions
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionThe friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionThe friction coefficient between plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then

View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)
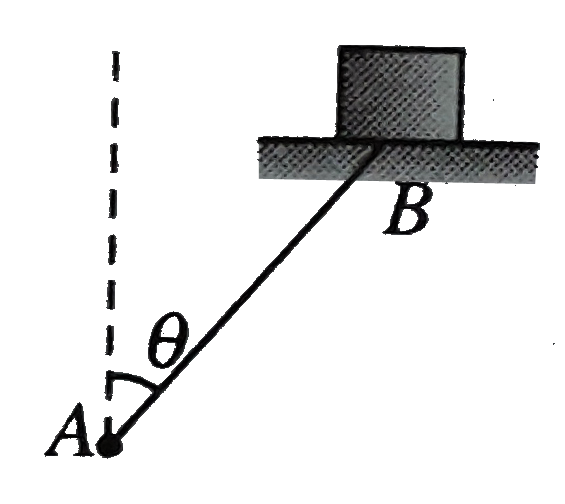
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)

View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionA car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road figure. A small bock of mass 100 g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is μ=0.58. a. Find the normal contact force exerted by the plate on the block. b. The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases Find the angle at which the block will just start sliding on the plate.

View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

View SolutionThe friction coefficient between the two blocks shown in figure is μ and the horizontal plane is smooth. A. If the system is slightly diplaced and released find the time period. B. find the magnitude of the frictional force between the blocks when the displacement from the mean position is x. c. What can be the maximum amplitude if the upper block does not slip relative to the lower block?
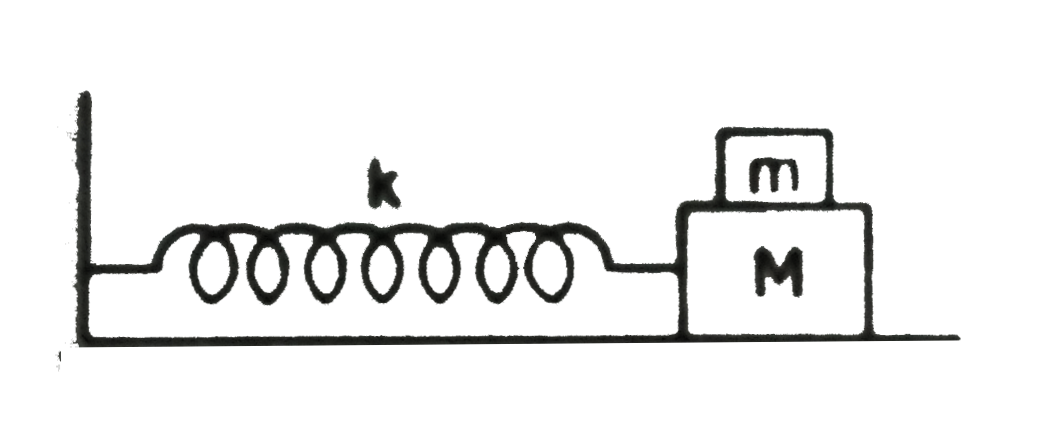
View SolutionTwo blocks a and B of mass mA=1kg and mB=3kg are kept on the table as shown in figure the coefficient of friction between A and B is 0.2 and between B and the surface of the table is also 0.2 the maximum force F that can be applied on B horizontally, so that the block A does not slide over the block B is [Take g=10m/s2]
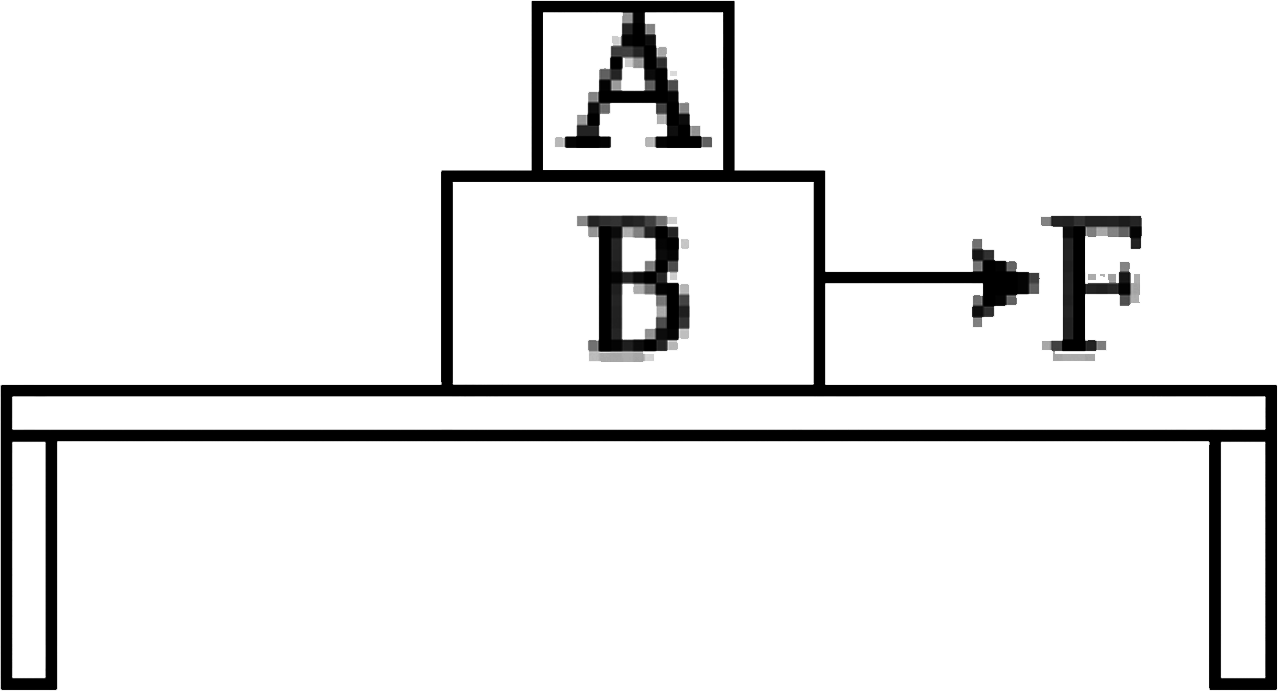
View Solution
