The Gaussian surface for calculating the electric field due to a charge distribution is
(a)any surface near the charge distribution
(b) always a spherical surface
(c) a symmetrical closed surface containing the charge distribution, at very point of which electric field has a single fixed value
(d) None of the given options
The correct Answer is:C
To solve the question regarding the Gaussian surface for calculating the electric field due to a charge distribution, we can follow these steps:
1. Understanding Gauss's Law:
Gauss's Law states that the electric flux through a closed surface is equal to the charge enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
ΦE=∮→E⋅d→A=Qencϵ0
where ΦE is the electric flux, →E is the electric field, d→A is the differential area vector, and Qenc is the enclosed charge.
2. Choosing a Gaussian Surface:
The Gaussian surface should be chosen based on the symmetry of the charge distribution. Common symmetrical shapes include:
- Spherical surfaces for point charges or uniformly charged spheres.
- Cylindrical surfaces for infinitely long charged wires.
- Planar surfaces for infinite charged planes.
3. Symmetry Consideration:
The key to applying Gauss's Law effectively is to ensure that the electric field has the same magnitude and direction at every point on the Gaussian surface. This is typically achieved when the surface is symmetrical with respect to the charge distribution.
4. Electric Field Calculation:
Once the appropriate Gaussian surface is selected, you can calculate the electric field by evaluating the surface integral of the electric field over the Gaussian surface. If the electric field is constant over the surface, the integral simplifies to:
ΦE=E⋅A
where A is the area of the Gaussian surface.
5. Conclusion:
Therefore, the Gaussian surface for calculating the electric field due to a charge distribution is a symmetrical closed surface that contains the charge distribution. The electric field at every point on this surface should ideally have a single fixed value.
Final Answer:
The Gaussian surface for calculating the electric field due to a charge distribution is a symmetrical closed surface containing the charge distribution, at every point of which the electric field has a single fixed value.
---
Gauss's Law states that the electric flux through a closed surface is equal to the charge enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
ΦE=∮→E⋅d→A=Qencϵ0
where ΦE is the electric flux, →E is the electric field, d→A is the differential area vector, and Qenc is the enclosed charge.
The Gaussian surface should be chosen based on the symmetry of the charge distribution. Common symmetrical shapes include:
- Spherical surfaces for point charges or uniformly charged spheres.
- Cylindrical surfaces for infinitely long charged wires.
- Planar surfaces for infinite charged planes.
The key to applying Gauss's Law effectively is to ensure that the electric field has the same magnitude and direction at every point on the Gaussian surface. This is typically achieved when the surface is symmetrical with respect to the charge distribution.
Once the appropriate Gaussian surface is selected, you can calculate the electric field by evaluating the surface integral of the electric field over the Gaussian surface. If the electric field is constant over the surface, the integral simplifies to:
ΦE=E⋅A
where A is the area of the Gaussian surface.
Therefore, the Gaussian surface for calculating the electric field due to a charge distribution is a symmetrical closed surface that contains the charge distribution. The electric field at every point on this surface should ideally have a single fixed value.
The Gaussian surface for calculating the electric field due to a charge distribution is a symmetrical closed surface containing the charge distribution, at every point of which the electric field has a single fixed value.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Calculate electric field due to a charge uniformly distributed in a spherical volume
View SolutionIt is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss's theorem because:
View SolutionElectric Field due to Dipole
View SolutionThe law goverening electrostatics is coulomb's law.In priciple coulomb's law can be used to compute electric field due to any charge configuation .In pracitce however it is a formidable task to compute electric field due to uniform charge distributions .For such cases Gauss proposed a theorem which states that
∮¯¯¯E.¯¯¯¯ds=qε0
where ds is an element of area directed across the outward normal for the surface at every point .The integral is called electric flux.Any convenient surface that we choose to evalute the surface integral is called the Gaussian surface.
The SI unit of electric flux is
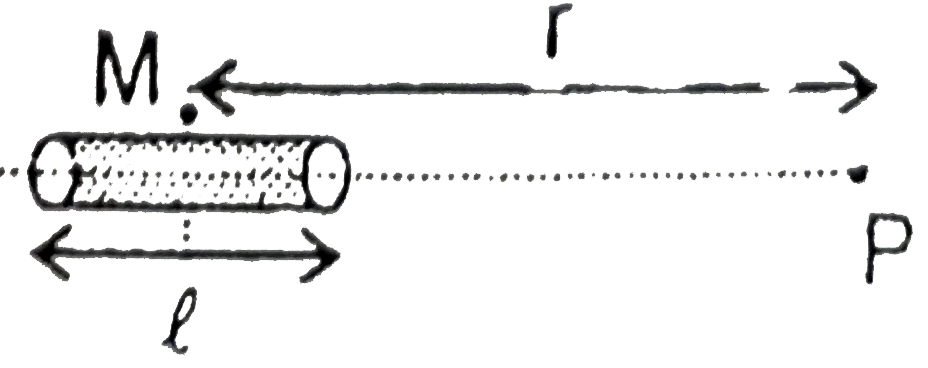
View SolutionA insulating cylindrical rod of diameter d and length l(l>>d) has a uniform surface charge density such that the electric field just outside the curved surface of the cylinder at point M is E0. Find the electric field due to charge distribuition at point P(r>>l).
View SolutionA charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.

View SolutionThe spatial distribution of the electric field due to charges (A,B) is shown in figure. Which of the following statements is correct?

View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionA charge is moved in an electric field of a fixed charge distribution from point A to another point B slowly. The work done by external agent in doing so is 100J . What is the change in potential energy of the charge as it moves from A to B ? What is the work done by the electric field of the charge distribution as the charge moves from A to B ?
View Solution
