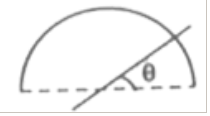
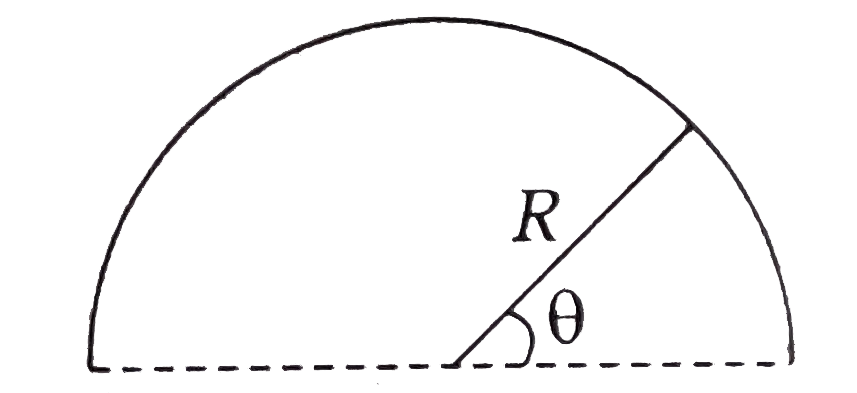
The moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle with the line joining its ends as shown in figure is
A
B
C
any angle
D
Text Solution
The correct Answer is:C
If we complete the ring, its mass become 2m
.
This value is independent of angle .
|
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2The moment of inertia of semicircular ring about its centre is
AMR2BMR22CMR24DNone of theseFind the moment of inortia of ring of mass m and radius R about an axis passing through its centre and making an angle of 45∘ with its plane:
 AMR24BMR22C34MR2DMR2
AMR24BMR22C34MR2DMR2
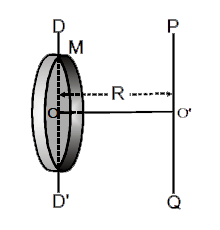
The moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution