The property of matter by virtue of which it does not regain its original shape and size after the removal of deforming force is called
deforming force
plasticity
elasticity
electricity
The correct Answer is:B
(c) The property of matter by virtue of whih it regains its original shape and size, when the deforming forces have been removed is called elasticity.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.215videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.315videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective10videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
The property of a body by virtue of which it tends to regain its original configuration as soon as the deforming forces applied on the body are removed is called elasticity. Coefficient of elasticity, E=stressstrain=F/aΔl/l=Flπr2(Δl) The value of E depends upon nature of material. A material with higher value of E is said to be more elastic. Read the above passage and answer the following question : (i) Which is more elastic steel or rubber ? Why ?
View SolutionThe delay in recovery on removal of the deforming force is called ___
View SolutionName the property of an object by virtue of which it opposes or tends to oppose any change in its state.
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
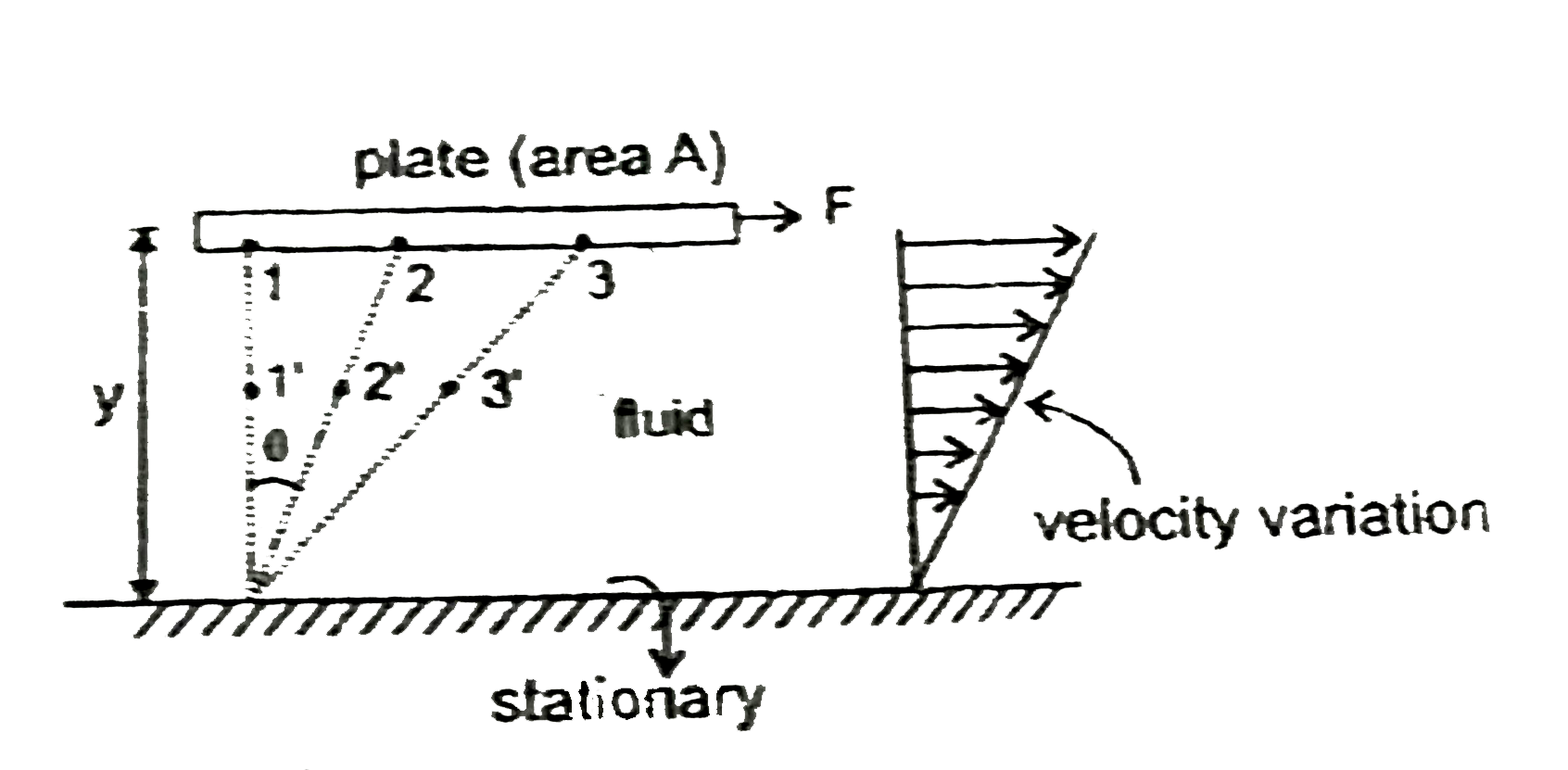
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
The velocity gradient just near the bottom boundary is equal to -View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
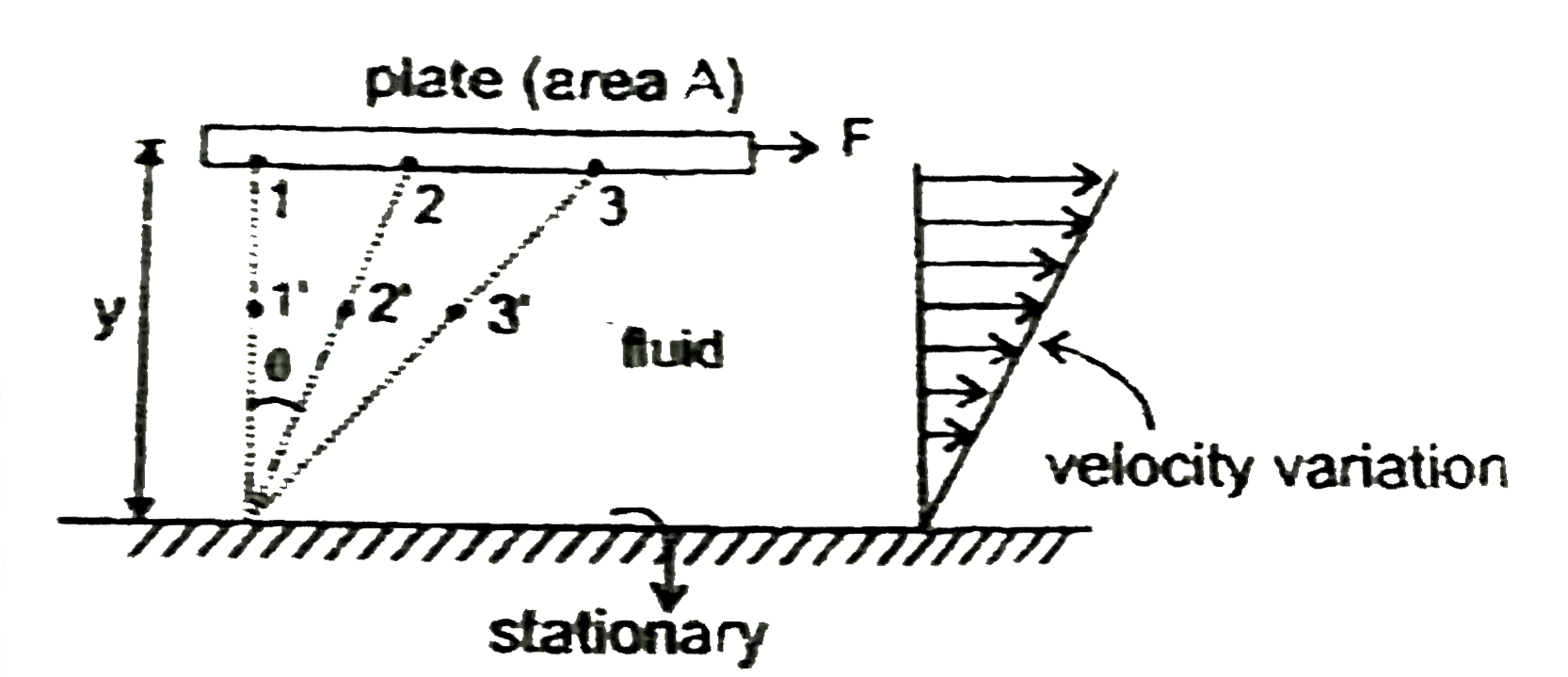
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
The velocity gradient just below the plate, in above problem is equal to - (per second)View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
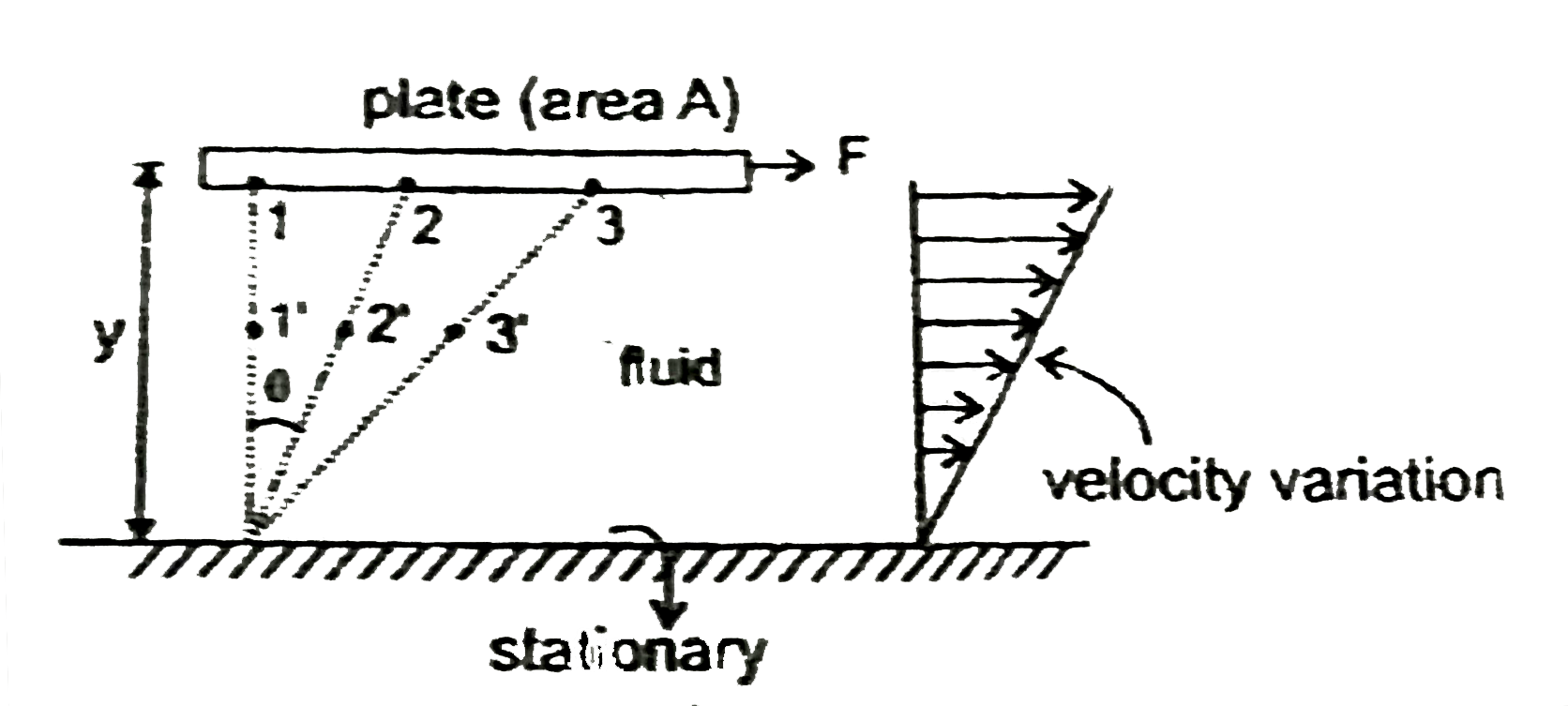
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
If velocity distribution is given as (parabolic)
u=c1y2+c2y+c3
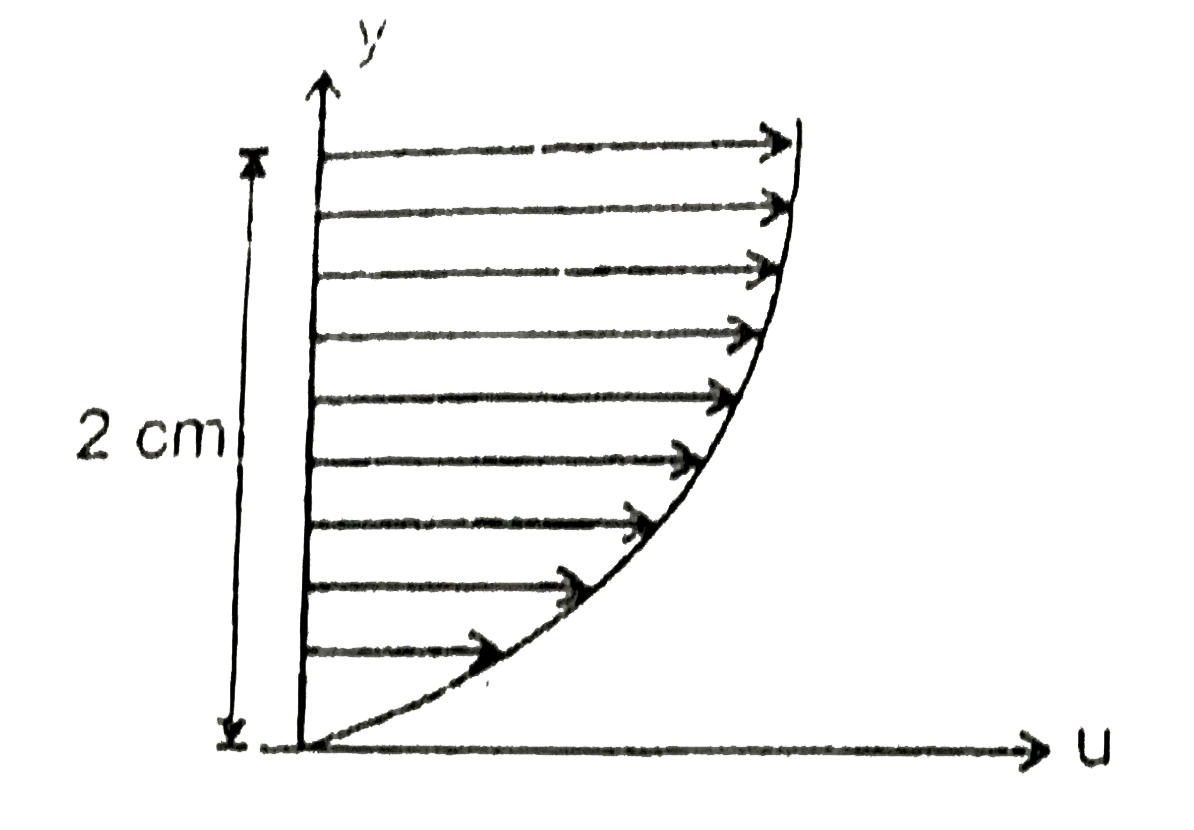For the same force of 2N and the speed of the plate 2m/sec, and area of plate is 1 and viscousity is .001, the constant C1,C2 & C3 are View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
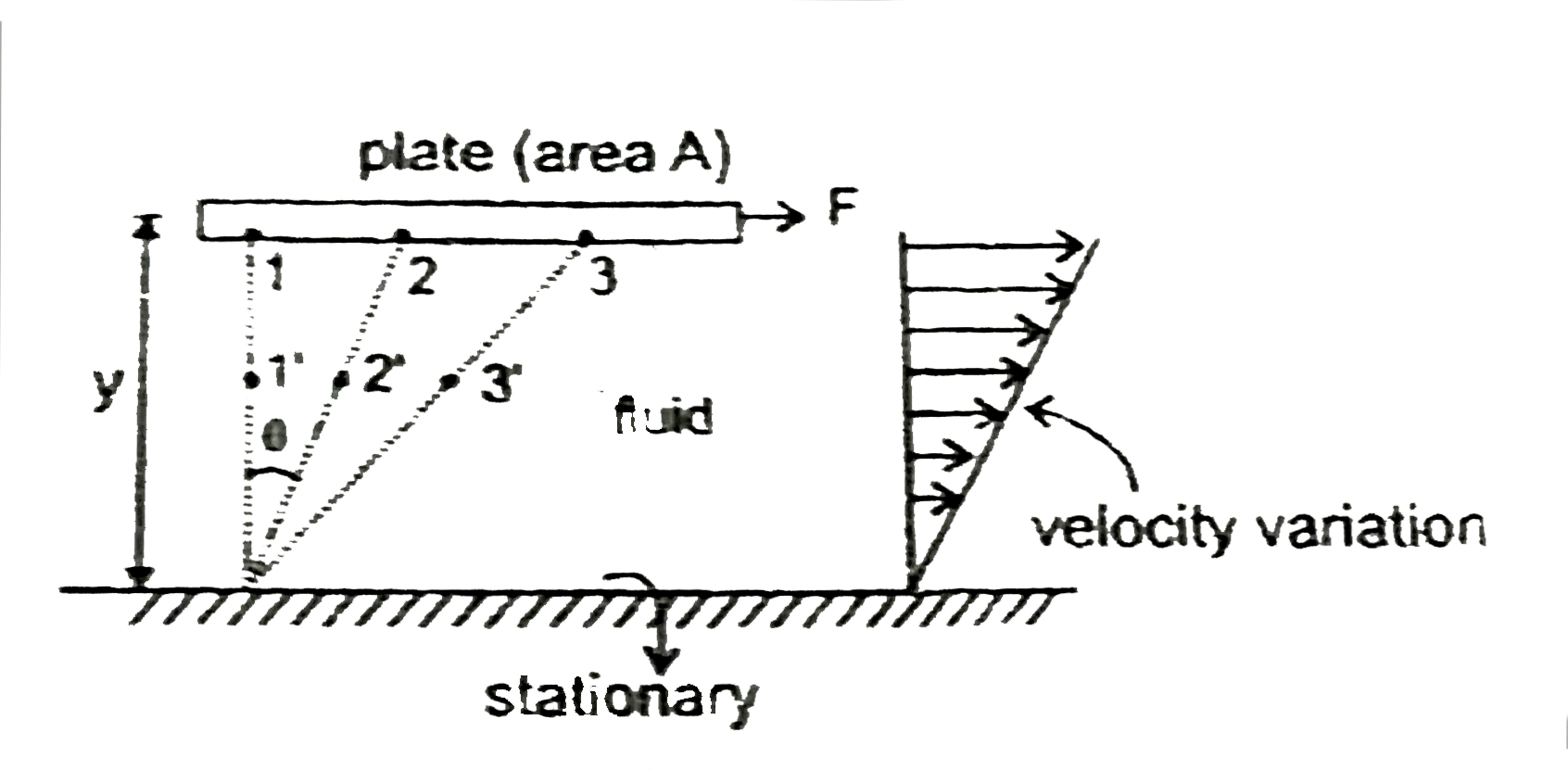
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
In the given figure if force of 2N required to maintain constant velocity of plate, the value of constant C1,&C2 are -
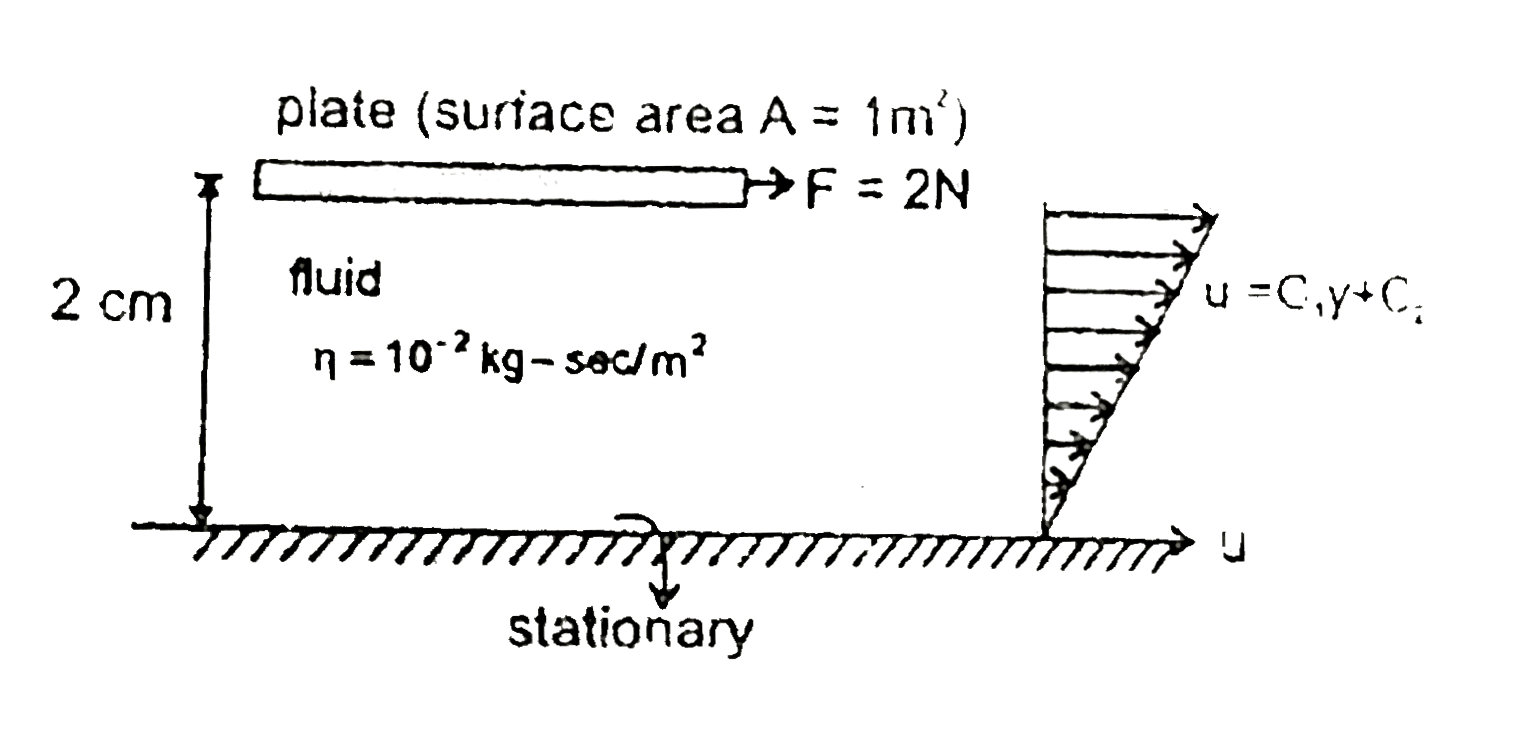View SolutionAssertion Upto the elastic limit, strain ∝ stress.
Reason Upto elastic limit, material returns to its original shape and size, when external force is removed.View SolutionThe one which does not lose its identity even after crystallisation is
View SolutionAssertion Upto elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed.
Reason Within elastic limit, the wire follows Hooke's law.View Solution