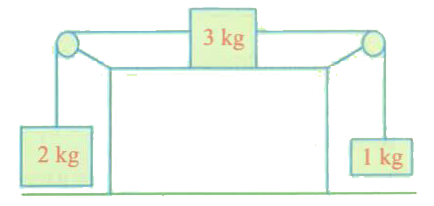
The system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

Video Solution
Text Solution
The correct Answer is:mgsinθM+2m(1−cosθ).
Let acceleration of the wedge be a leftwards then acceleration of block, relative to the wedge will also be equal to a but down the incline. Hence, net acceleration of the block will be equal to vector sum of these two as shown in fig.
Now considering FBD's

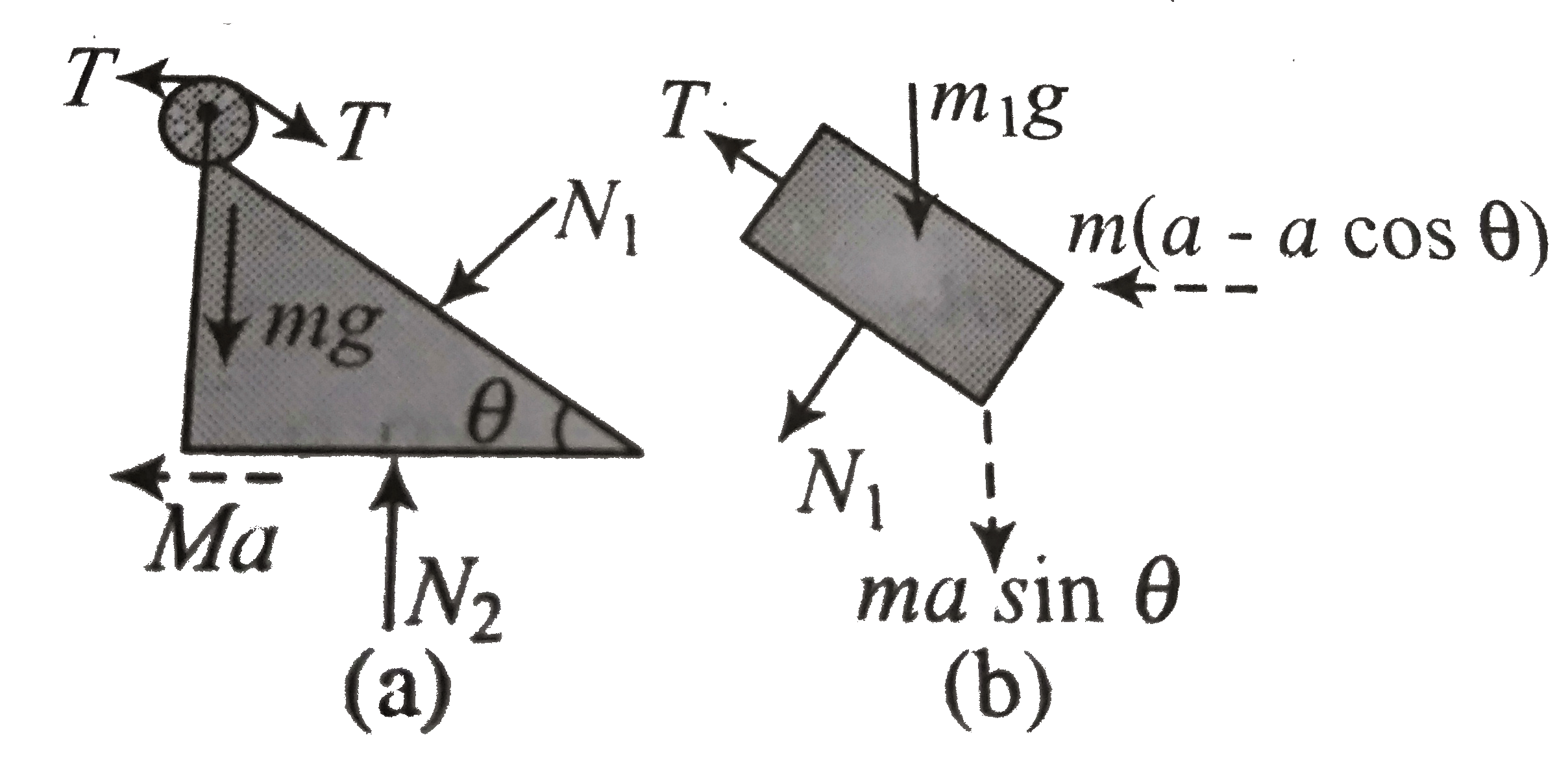
For the wedge,
N2=Tsinθ+N1cosθ..(i)
T−Tcosθ+N1sinθ=Ma ..(ii)
For the block,
mg−N1cosθ=masinθ ..(iii)
Tcosθ−N1sinθ=m(a−acosθ)
Solving above equation, a=mgsinθM+2m(1−cosθ).
|
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
76 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Knowledge Check
The tension in the string in the pulley system shown in
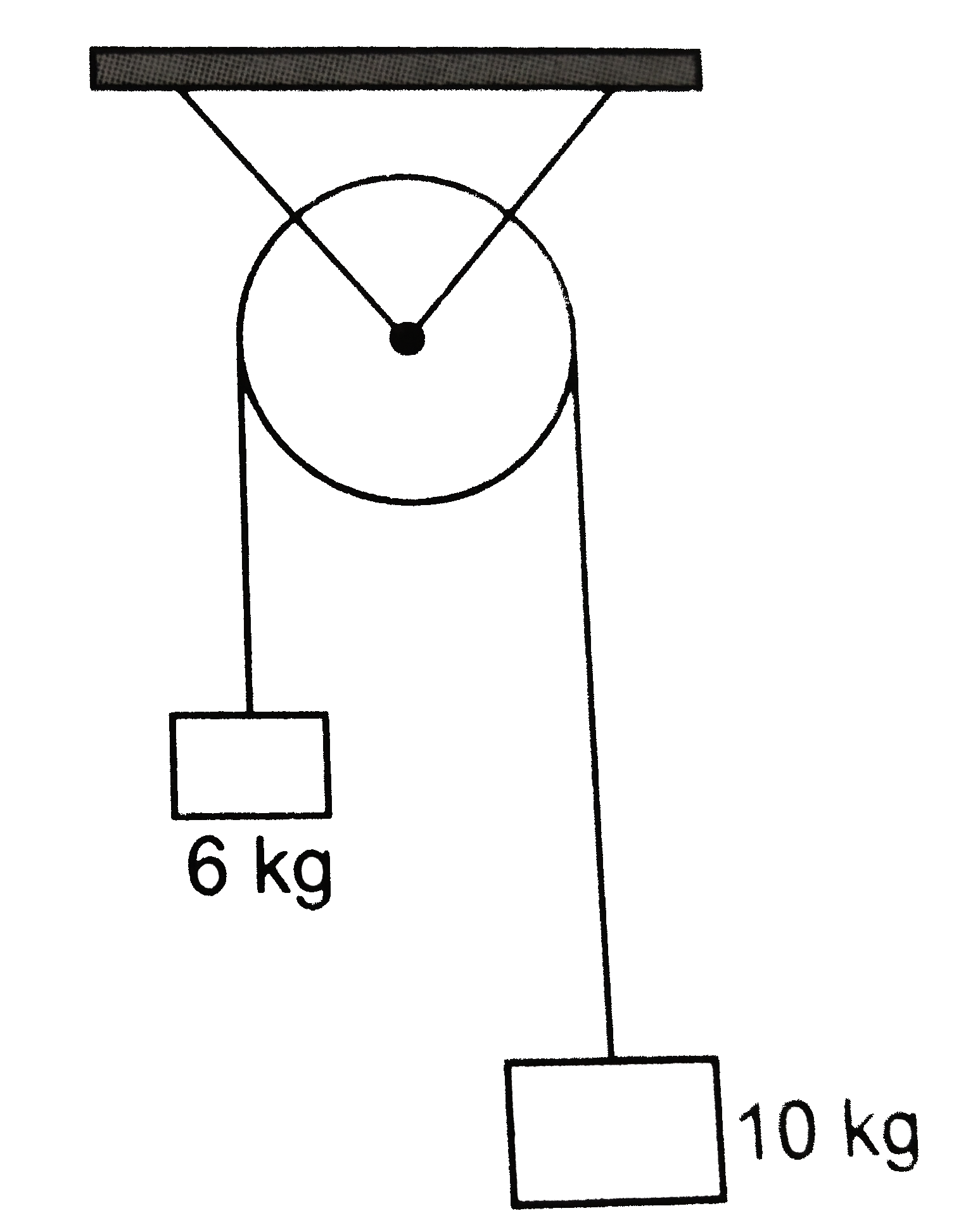 .A5.7NB7NC7.5ND73.5N
.A5.7NB7NC7.5ND73.5NThe system shown in th fig is released from rest. (Neglecting friction and mass of the pulley, string and spring). The spring can be elongated:
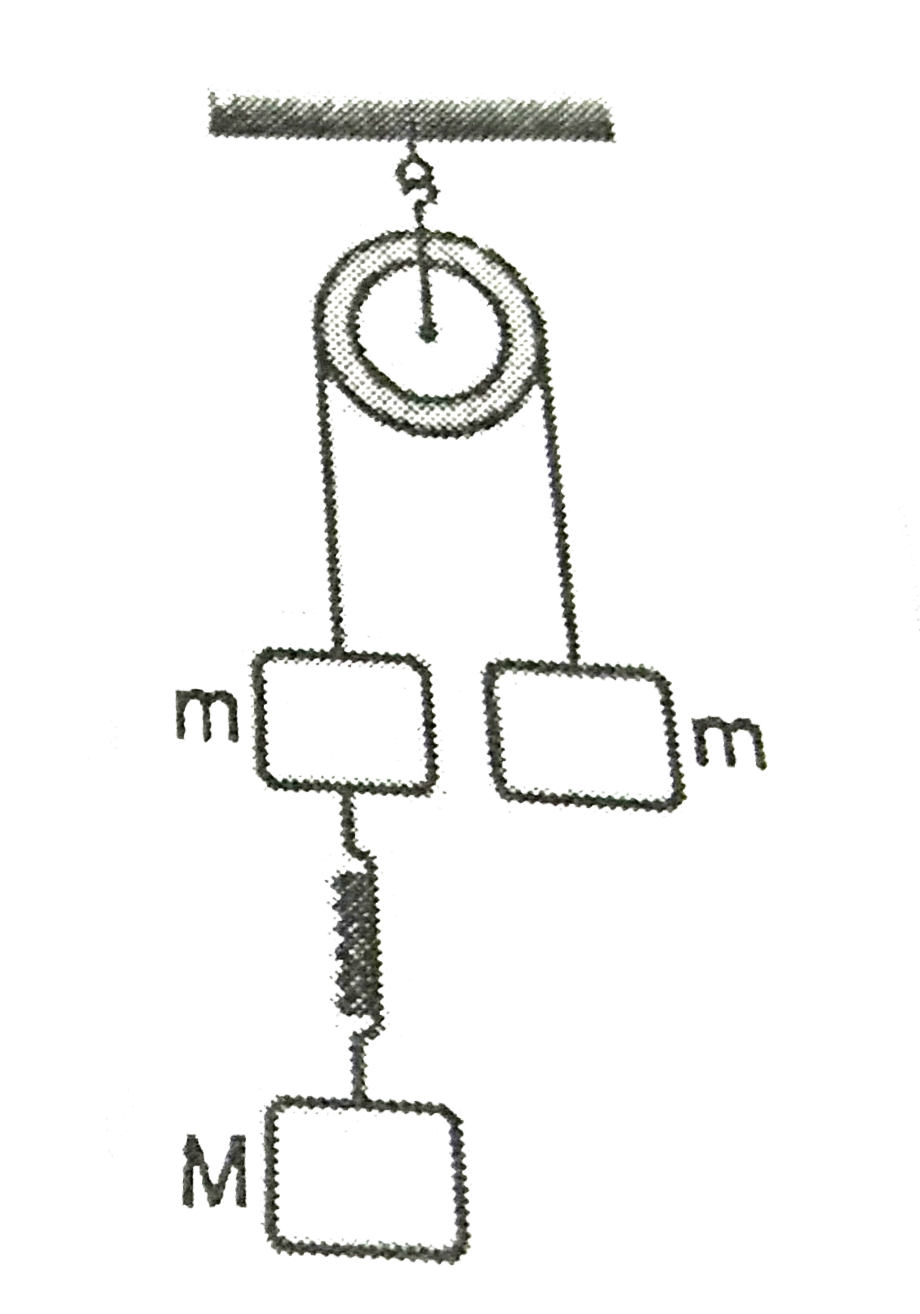 Aif M>mBif M>2mCif M>m2Dfor any value of M (M should be greater than zero)
Aif M>mBif M>2mCif M>m2Dfor any value of M (M should be greater than zero)
In the system shown in figure, the block A is released from rest. Find
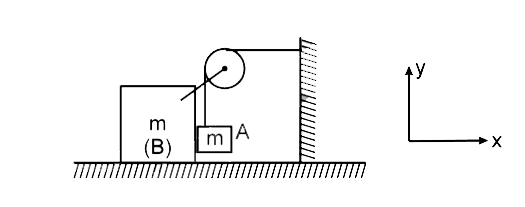
Tension in the string.
View SolutionThe force exerted by the ideal string on the ideal pulley P shown in the figure is

View SolutionFind the acceleration and tension in the string in the following cases . The pulley and string are massless.
(a)
(b)
View SolutionFind the acceleration blocks in fig. The pulley and the string are massless.

View SolutionThe system shown in figure is released is released from rest . Find acceleration of different string blocks and tenson in different strings.

View SolutionFor the system shown in the figure,the pulleys are light and frictionless.The tension in the string will be
View Solution