The triangular plate described in the last question has angle <A=θ. Now find its moment of inertia about an axis through A perpendicular to the plane of the plate.
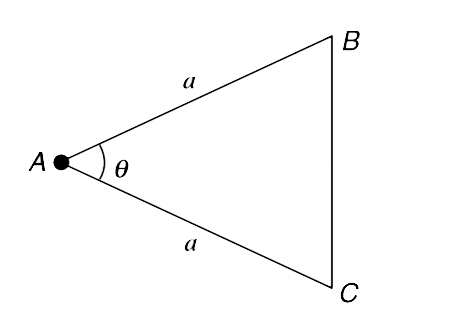
The correct Answer is:12Ma2(1−23sin2(θ)2)
Step by step video, text & image solution for The triangular plate described in the last question has angle lt A = theta. Now find its moment of inertia about an axis through A perpendicular to the plane of the plate. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
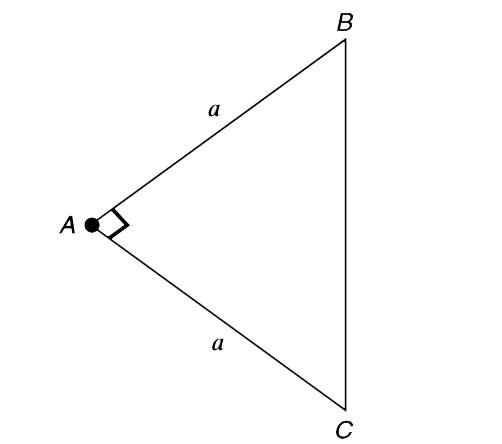
ABC is an isosceles triangle right angled at A. Mass of the triangular plate is M and its equal sides are of length a. Find the moment of inertia of this plate about an axis through A perpendicular to the plane of the plate. Use the expression of moment of inertia for a square plate that you might have studied.
View SolutionA uniform rectangular plate has moment of inertia about its longer side, equal to I. The moment of inertia of the plate about an axis in its plane, passing through the centre and parallel to the shorter sides is also equal to I. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
View Solution
Knowledge Check
Find the ratio of moment of inertia about axis perpendicular to rectangular plate passing through O & O
 A12B13C14D18
A12B13C14D18The diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
 A43Ma2BI+14Ma2C2IDI2
A43Ma2BI+14Ma2C2IDI2What is the moment of inertia of a triangular plate ABC of mass M and side BC='a' about a axis passing through A and perpedicular to the plane of the plate?
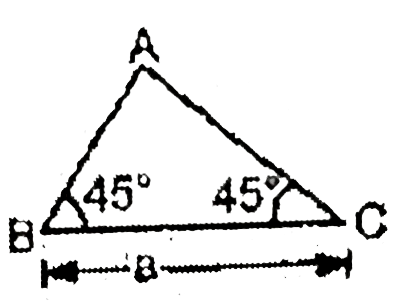 AMa26B3Ma24CMa224DMa212
AMa26B3Ma24CMa224DMa212
Moment of inertia of a rectangular plate about an axis passing through P and perpendicular to the plate is I. Moment of PQR about an axis perpendicular to the plane of the plate :
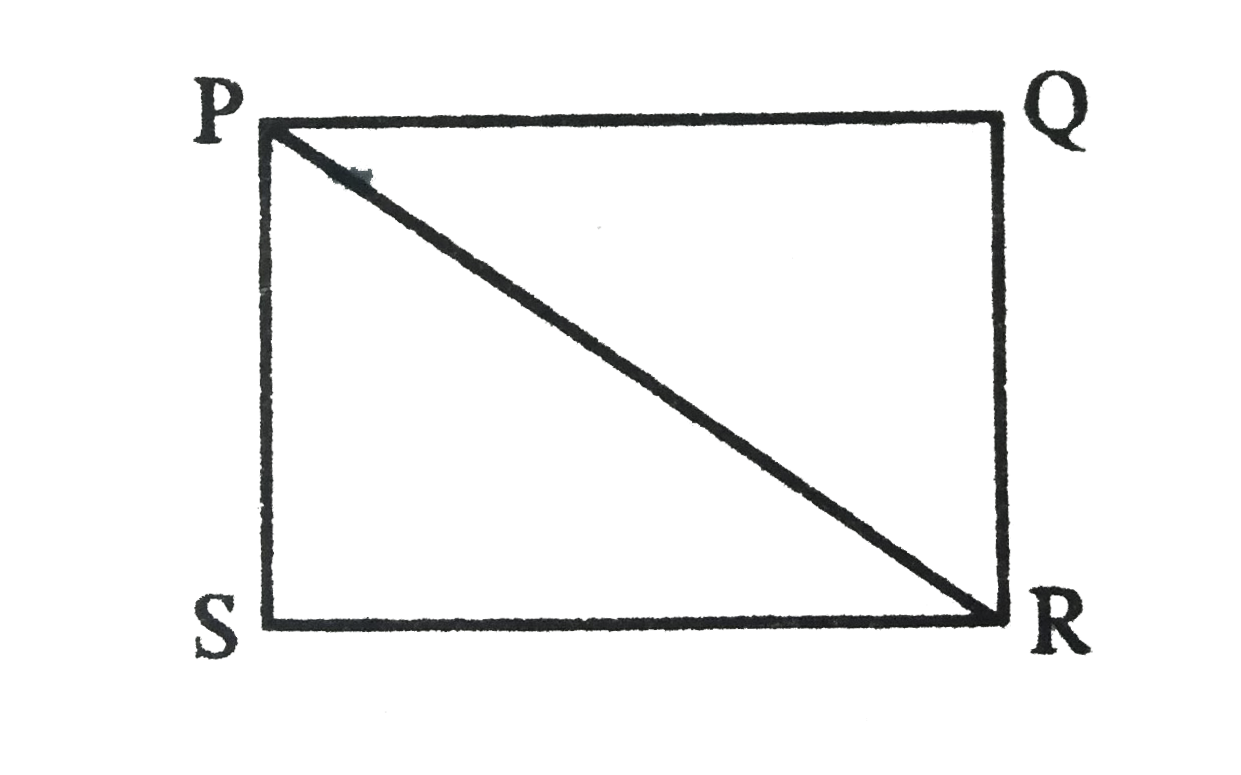 .
.
View SolutionA solid cylinder has diameter D and length L. Find its moment of inertia about an axis perpendicular to its length and passing through the centre of gravity.
View SolutionA hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane

View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionMoment of inertia of a circular ring about an axis through its centre and perpendicular to its plane is
View Solution
