What is potential at a distance r(<R) in a dielectric sphere of uniform charge density ρ, radius R and dielectric constant εr.
To find the potential at a distance r (where r<R) inside a dielectric sphere of uniform charge density ρ, radius R, and dielectric constant ϵr, we can follow these steps:
Step 1: Understand the Setup
We have a sphere of radius R with a uniform charge density ρ. We need to find the electric potential at a point inside the sphere at a distance r from the center.
Step 2: Determine the Total Charge Inside the Sphere
The total charge Q within a sphere of radius R is given by:
Q=ρ⋅Volume=ρ⋅(43πR3)
Step 3: Calculate the Electric Field Inside the Sphere
Using Gauss's Law, the electric field E at a distance r from the center (where r<R) is given by:
E=Qenc4πϵ0ϵrr2
where Qenc is the charge enclosed within radius r:
Qenc=ρ⋅(43πr3)
Thus,
E=ρ⋅(43πr3)4πϵ0ϵrr2=ρr3ϵ0ϵr
Step 4: Calculate the Potential Difference
The potential difference VB−VA between a point B on the surface of the sphere (at r=R) and a point A inside the sphere (at r) can be calculated using:
VB−VA=−∫rREdr
Substituting the expression for E:
VB−VA=−∫rRρr3ϵ0ϵrdr
Step 5: Evaluate the Integral
Evaluating the integral:
VB−VA=−(ρ3ϵ0ϵr⋅r22)rR=−ρ6ϵ0ϵr(r2−R2)
Step 6: Find the Potential at Point A
The potential at point A (inside the sphere) can be expressed as:
VA=VB+(VB−VA)
Assuming the potential at the surface VB is given by:
VB=Q4πϵ0R=ρ⋅(43πR3)4πϵ0R=ρR23ϵ0
Thus,
VA=ρR23ϵ0−ρ6ϵ0ϵr(r2−R2)
Step 7: Simplify the Expression
Combining the terms, we get:
VA=ρR23ϵ0−ρ6ϵ0ϵrr2+ρR26ϵ0ϵr
This can be simplified to:
VA=ρ6ϵ0(2R2+R2ϵr−r2)
Final Result
Thus, the potential at a distance r inside the dielectric sphere is:
VA=ρ6ϵ0(2R2+R2ϵr−r2)
We have a sphere of radius R with a uniform charge density ρ. We need to find the electric potential at a point inside the sphere at a distance r from the center.
The total charge Q within a sphere of radius R is given by:
Q=ρ⋅Volume=ρ⋅(43πR3)
Using Gauss's Law, the electric field E at a distance r from the center (where r<R) is given by:
E=Qenc4πϵ0ϵrr2
where Qenc is the charge enclosed within radius r:
Qenc=ρ⋅(43πr3)
Thus,
E=ρ⋅(43πr3)4πϵ0ϵrr2=ρr3ϵ0ϵr
The potential difference VB−VA between a point B on the surface of the sphere (at r=R) and a point A inside the sphere (at r) can be calculated using:
VB−VA=−∫rREdr
Substituting the expression for E:
VB−VA=−∫rRρr3ϵ0ϵrdr
Evaluating the integral:
VB−VA=−(ρ3ϵ0ϵr⋅r22)rR=−ρ6ϵ0ϵr(r2−R2)
The potential at point A (inside the sphere) can be expressed as:
VA=VB+(VB−VA)
Assuming the potential at the surface VB is given by:
VB=Q4πϵ0R=ρ⋅(43πR3)4πϵ0R=ρR23ϵ0
Thus,
VA=ρR23ϵ0−ρ6ϵ0ϵr(r2−R2)
Combining the terms, we get:
VA=ρR23ϵ0−ρ6ϵ0ϵrr2+ρR26ϵ0ϵr
This can be simplified to:
VA=ρ6ϵ0(2R2+R2ϵr−r2)
Thus, the potential at a distance r inside the dielectric sphere is:
VA=ρ6ϵ0(2R2+R2ϵr−r2)
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example3videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 179videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
Similar Questions
A solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnetude) at point 'C' inside the cavity
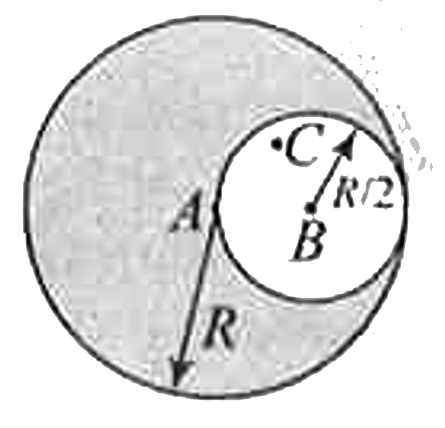 View Solution
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
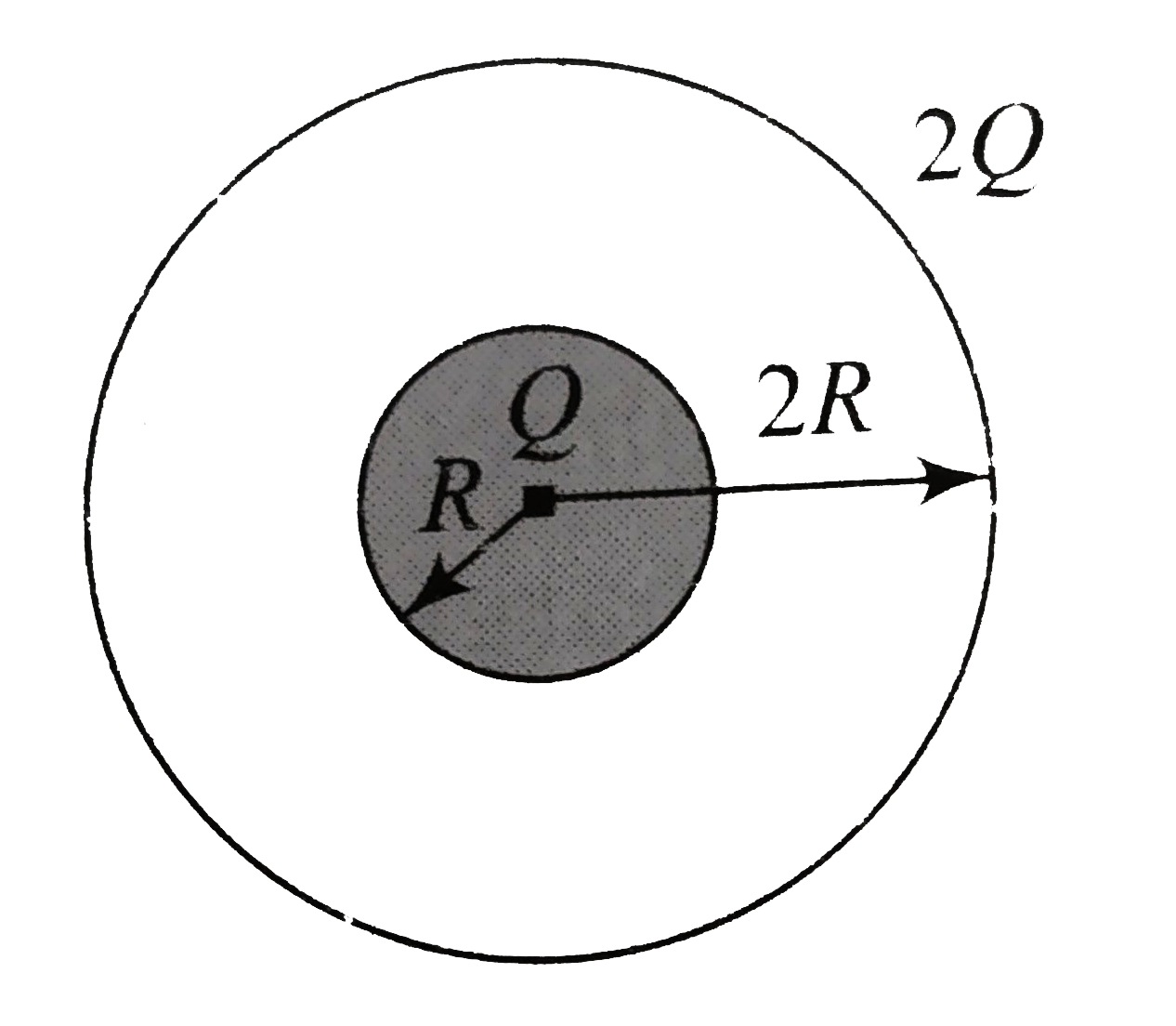 View Solution
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?
 View Solution
View SolutionFind V and E at point r where : (Q is a point charge kept at the centre of the non-conducting neutral thick sphere of inner radius 'a' and outer radius 'b') (dielectric constant =∈r)

(i) 0<r<a (ii)a≤r<b (iii)r≥bView SolutionIf →a and →b are two unit vectors and θ is the angle between them, then the unit vector along the angular bisector of →a and →b will be given by
View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View SolutionPotential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
View SolutionA and C are concentric conducting spherical shells of radius a and c respectively.A is sueeounded by a concentric dielectric medium of inner radius a, outer radius b and dielectric constant k. If sphere A is given a charge Q, the potential at the outer surface of the dielectric is
 View Solution
View Solution

