Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
connecting them in parallel
connecting two in series and one in parallel
connecting two in parallel and one in series
connecting all of them in series
The correct Answer is:B
To solve the problem of connecting three capacitors of 4 µF each to achieve an effective capacitance of 6 µF, we need to analyze the possible configurations: series and parallel connections.
1. Understanding Capacitor Configurations:
- When capacitors are connected in parallel, the total capacitance (C_eq) is the sum of the individual capacitances:
Ceq=C1+C2+C3
- When capacitors are connected in series, the total capacitance is given by:
1Ceq=1C1+1C2+1C3
2. Calculating Maximum Capacitance:
- For three capacitors of 4 µF connected in parallel:
Ceq=4+4+4=12μF
- This configuration gives the maximum capacitance.
3. Calculating Minimum Capacitance:
- For three capacitors of 4 µF connected in series:
1Ceq=14+14+14=34
Ceq=43μF≈1.33μF
- This configuration gives the minimum capacitance.
4. Finding a Combination to Achieve 6 µF:
- We need to find a combination of series and parallel connections to achieve an effective capacitance of 6 µF.
- One possible way is to connect two capacitors in parallel and one in series with that combination.
5. Calculating the Effective Capacitance for the Combination:
- Connect two capacitors in parallel:
Cparallel=4+4=8μF
- Now, connect this parallel combination in series with the third capacitor:
1Ceq=18+14
- Finding a common denominator (8):
1Ceq=18+28=38
Ceq=83μF≈2.67μF
- This does not give us the required capacitance.
6. Trying Another Configuration:
- Connect one capacitor in series with two capacitors in parallel:
- Two capacitors in parallel:
Cparallel=4+4=8μF
- Now connect this in series with the third capacitor:
1Ceq=18+14
1Ceq=18+28=38
Ceq=83μF≈2.67μF
- This is still not yielding 6 µF.
7. Final Configuration:
- Connect two capacitors in series:
1Cseries=14+14=12⟹Cseries=2μF
- Now connect this series combination in parallel with the third capacitor:
Ceq=Cseries+Cthird=2+4=6μF
Conclusion:
To achieve an effective capacitance of 6 µF, connect two capacitors in series (2 µF) and then connect this combination in parallel with the third capacitor (4 µF).
- When capacitors are connected in parallel, the total capacitance (C_eq) is the sum of the individual capacitances:
Ceq=C1+C2+C3
- When capacitors are connected in series, the total capacitance is given by:
1Ceq=1C1+1C2+1C3
- For three capacitors of 4 µF connected in parallel:
Ceq=4+4+4=12μF
- This configuration gives the maximum capacitance.
- For three capacitors of 4 µF connected in series:
1Ceq=14+14+14=34
Ceq=43μF≈1.33μF
- This configuration gives the minimum capacitance.
- We need to find a combination of series and parallel connections to achieve an effective capacitance of 6 µF.
- One possible way is to connect two capacitors in parallel and one in series with that combination.
- Connect two capacitors in parallel:
Cparallel=4+4=8μF
- Now, connect this parallel combination in series with the third capacitor:
1Ceq=18+14
- Finding a common denominator (8):
1Ceq=18+28=38
Ceq=83μF≈2.67μF
- This does not give us the required capacitance.
- Connect one capacitor in series with two capacitors in parallel:
- Two capacitors in parallel:
Cparallel=4+4=8μF
- Now connect this in series with the third capacitor:
1Ceq=18+14
1Ceq=18+28=38
Ceq=83μF≈2.67μF
- This is still not yielding 6 µF.
- Connect two capacitors in series:
1Cseries=14+14=12⟹Cseries=2μF
- Now connect this series combination in parallel with the third capacitor:
Ceq=Cseries+Cthird=2+4=6μF
To achieve an effective capacitance of 6 µF, connect two capacitors in series (2 µF) and then connect this combination in parallel with the third capacitor (4 µF).
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionSeven capacitors, each a of a cpacitance 2μF, are to be connected in a configuration to obatin an effective capacitance of (1613)μF. Which of the combinations, shown in figure below, will achieve the desired value ?
View SolutionThe effective capacitence in μF in between A and B will be
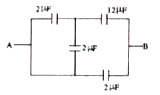
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
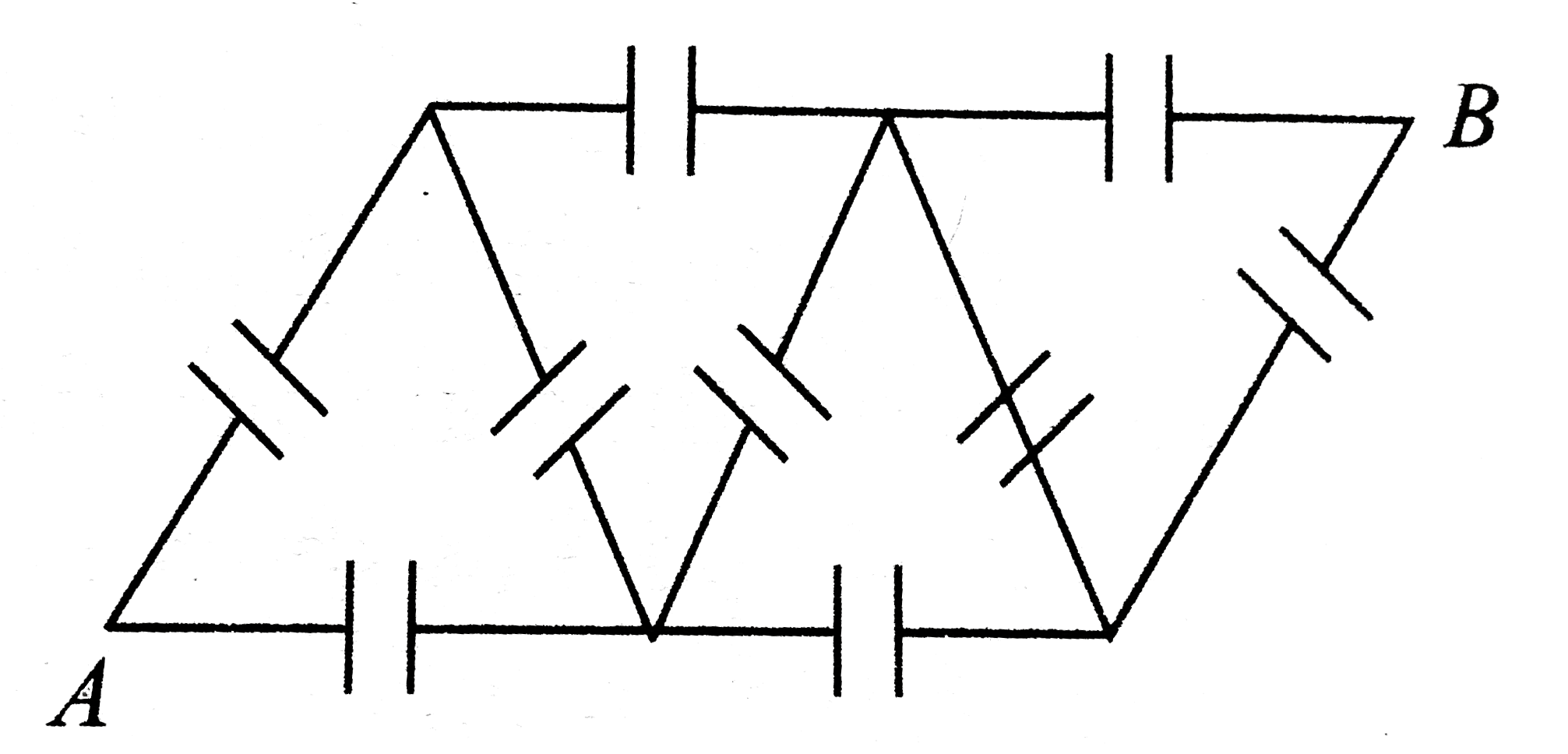 .
.
View SolutionThree capacitors 2μF,3μFand6μF are joined with each other. What is the minimum effective capacitance?
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View SolutionFour capacitors each of capacity 8μF area connected with each other as shown in figure. The equivalent capacitance between points X and Y will be

View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View SolutionFour capacitors of each of capacity 3μF are connected as shown in the adjoining figure. The ratio of equivalent capacitance between A and B and between A and C will be

View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
View Solution


