Three capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
2:49
49:2
4:49
49:4
The correct Answer is:C
To find the ratio of the equivalent capacitances of three capacitors connected in series and in parallel, we can follow these steps:
Step 1: Calculate the equivalent capacitance in series
For capacitors connected in series, the formula for the equivalent capacitance Cs is given by:
1Cs=1C1+1C2+1C3
Given the capacitances:
- C1=1μF
- C2=2μF
- C3=4μF
Substituting the values into the formula:
1Cs=11+12+14
Finding a common denominator (which is 4):
1Cs=44+24+14=4+2+14=74
Now, taking the reciprocal to find Cs:
Cs=47μF
Step 2: Calculate the equivalent capacitance in parallel
For capacitors connected in parallel, the equivalent capacitance Cp is simply the sum of the individual capacitances:
Cp=C1+C2+C3
Substituting the values:
Cp=1+2+4=7μF
Step 3: Calculate the ratio of equivalent capacitances
Now, we need to find the ratio of the equivalent capacitance in series to that in parallel:
Ratio=CsCp=477
This simplifies to:
Ratio=47×17=449
Final Answer
Thus, the ratio of the equivalent capacitances of the capacitors in series to that in parallel is:
449
For capacitors connected in series, the formula for the equivalent capacitance Cs is given by:
- C1=1μF
- C2=2μF
- C3=4μF
For capacitors connected in parallel, the equivalent capacitance Cp is simply the sum of the individual capacitances:
Now, we need to find the ratio of the equivalent capacitance in series to that in parallel:
Thus, the ratio of the equivalent capacitances of the capacitors in series to that in parallel is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
View SolutionTwo identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
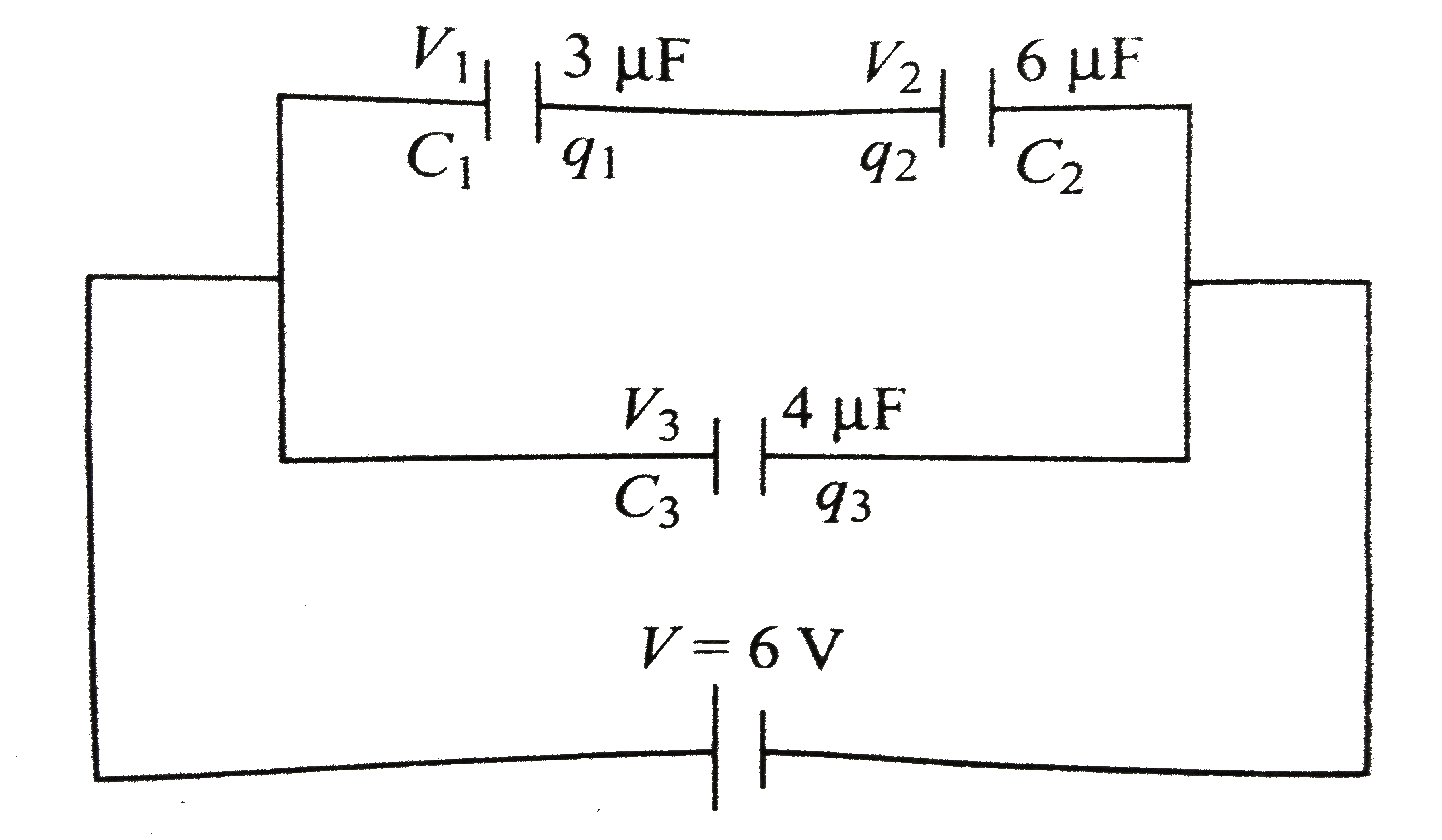
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionA series combination of three capacitors of capacities 1μF,2μF and 8μF is connected to a battery of e.m.f. 13 volt .The potential difference across the plates of 2μF capacitor will be
View SolutionThree capcitors of capacitances 4μF,
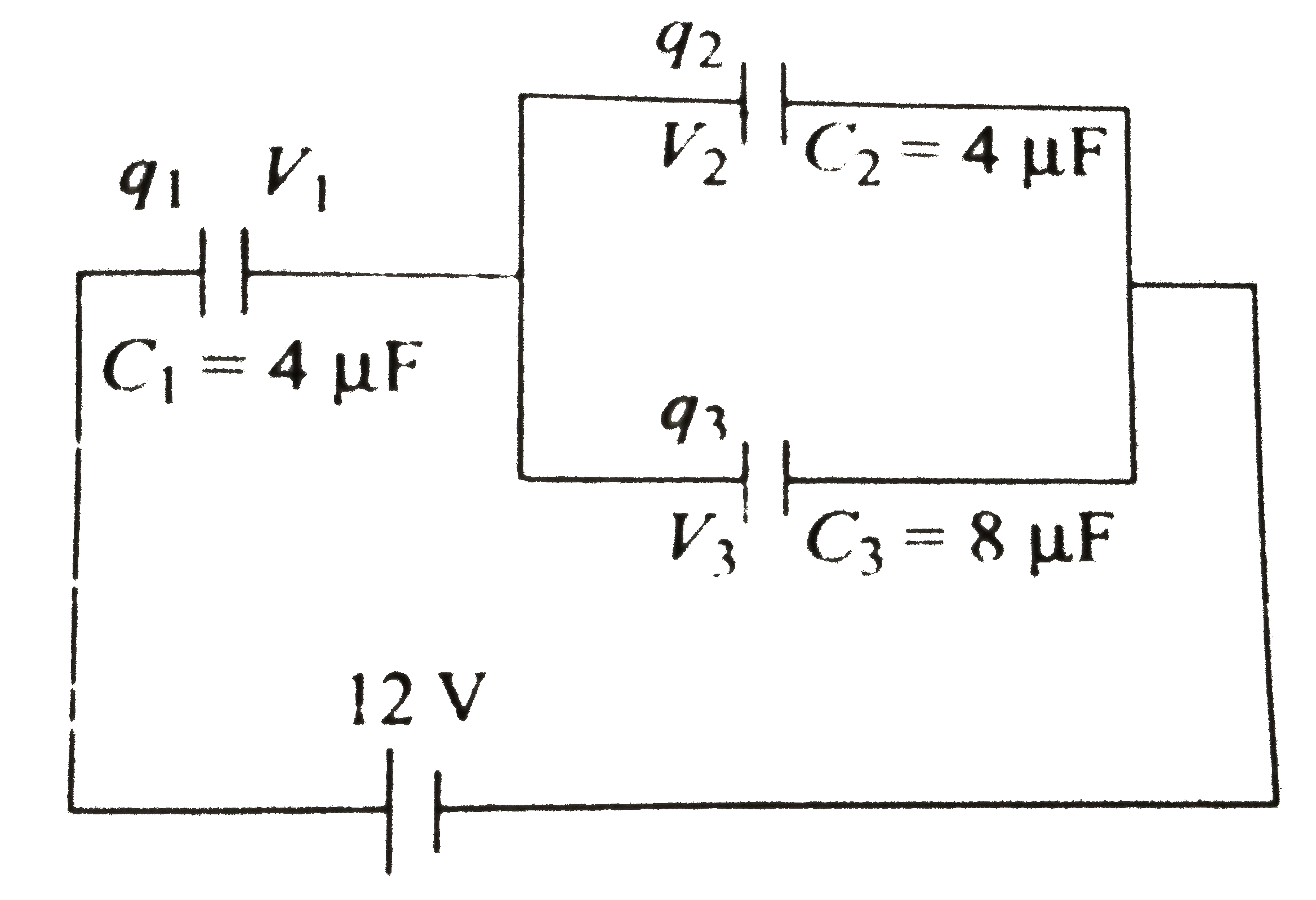 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?
View Solution
