Three concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
1:2:3
1:3:5
1:4:9
1:8:18
The correct Answer is:B
To solve the problem, we need to find the ratio of the charges Q1:Q2:Q3 on three concentric metallic spherical shells with radii R,2R, and 3R respectively, given that the surface charge densities on the outer surfaces of the shells are equal.
1. Understanding Surface Charge Density:
The surface charge density σ on a spherical shell is defined as:
σ=QA
where Q is the charge on the shell and A is the surface area of the shell.
2. Calculating Surface Areas:
The surface area A of a sphere is given by 4πr2. Therefore, the surface areas for the three shells are:
- For the first shell (radius R):
A1=4πR2
- For the second shell (radius 2R):
A2=4π(2R)2=16πR2
- For the third shell (radius 3R):
A3=4π(3R)2=36πR2
3. Setting Up the Equation for Equal Surface Charge Densities:
Since the surface charge densities are equal, we can write:
σ1=σ2=σ3
This gives us the equations:
Q14πR2=Q216πR2=Q336πR2
4. Simplifying the Equations:
We can cancel 4πR2 from each term:
Q1=k⋅4(1)
Q2=k⋅16(2)
Q3=k⋅36(3)
where k is a constant.
5. Finding the Ratios:
Now we can express the charges in terms of k:
- From (1): Q1=4k
- From (2): Q2=16k
- From (3): Q3=36k
Therefore, the ratio of the charges is:
Q1:Q2:Q3=4k:16k:36k
Simplifying this gives:
Q1:Q2:Q3=4:16:36
Dividing each term by 4:
Q1:Q2:Q3=1:4:9
Final Answer:
The ratio of the charges given to the shells is:
Q1:Q2:Q3=1:4:9
The surface charge density σ on a spherical shell is defined as:
σ=QA
where Q is the charge on the shell and A is the surface area of the shell.
The surface area A of a sphere is given by 4πr2. Therefore, the surface areas for the three shells are:
- For the first shell (radius R):
A1=4πR2
- For the second shell (radius 2R):
A2=4π(2R)2=16πR2
- For the third shell (radius 3R):
A3=4π(3R)2=36πR2
Since the surface charge densities are equal, we can write:
σ1=σ2=σ3
This gives us the equations:
Q14πR2=Q216πR2=Q336πR2
We can cancel 4πR2 from each term:
Q1=k⋅4(1)
Q2=k⋅16(2)
Q3=k⋅36(3)
where k is a constant.
Now we can express the charges in terms of k:
- From (1): Q1=4k
- From (2): Q2=16k
- From (3): Q3=36k
Q1:Q2:Q3=4k:16k:36k
Simplifying this gives:
Q1:Q2:Q3=4:16:36
Dividing each term by 4:
Q1:Q2:Q3=1:4:9
The ratio of the charges given to the shells is:
Q1:Q2:Q3=1:4:9
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Three concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionConcentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThree concentric conducting spherical shells of radii R,2R carry charges Q, -2Q and 3Q, respectively. Find the electric potential at r = R and at r = 3 R, where r is the radii distance from the centre.

View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solutionthere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
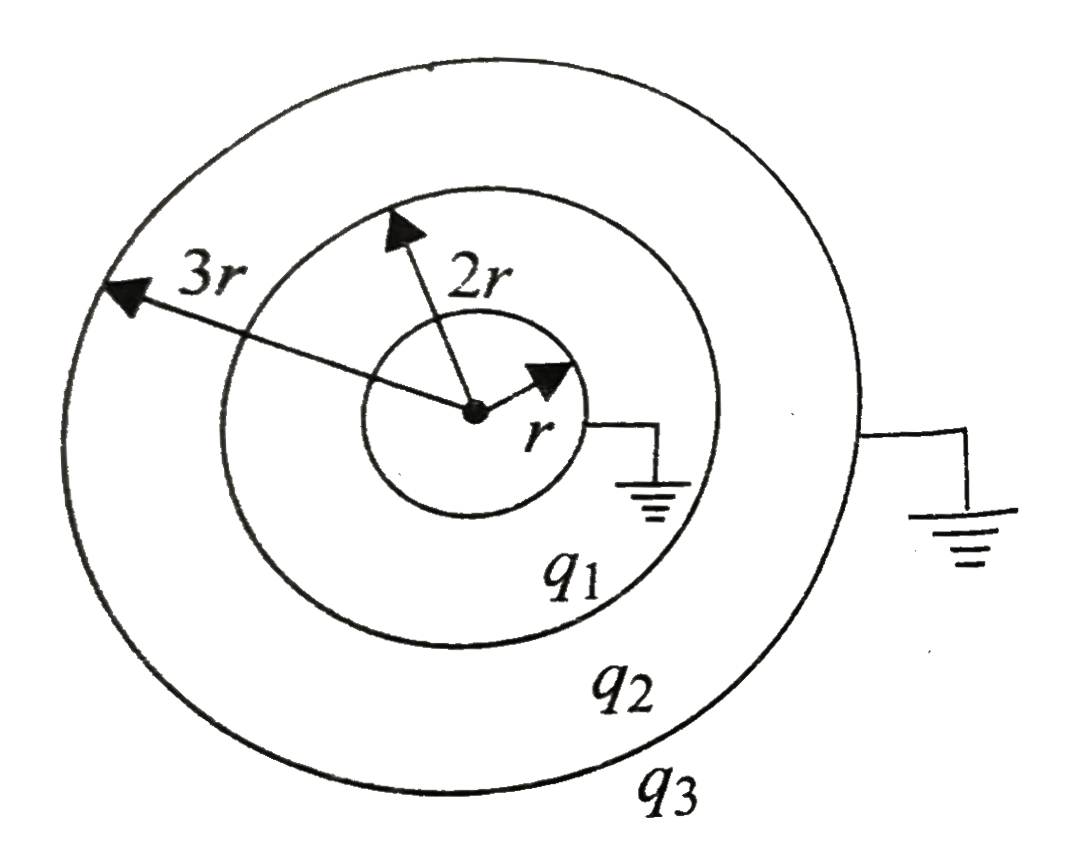
View SolutionThree concentric conducting spherical shells have radii r, 2r, and 3r and charges q1,q2andq3, respectively. Innermost and outermost shells are earthed as shown in figure. The charges shown are after earthing. Select the correct alternative.
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View Solution
