Three identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of . What charges should be imparted to the balls for each thread to form an angle of with the vertical?
The correct Answer is:A, C
To solve the problem, we need to find the charge that should be imparted to each of the three identical small balls so that they form an angle of α=30∘ with the vertical when suspended by silk threads of length l=20cm.
1. Convert Units:
- Convert the mass of each ball from grams to kilograms:
m=0.1g=0.1×10−3kg=10−4kg
- Convert the length of the thread from centimeters to meters:
l=20cm=0.2m
2. Determine the Geometry:
- The angle α=30∘ implies that each ball will be at a distance R from the vertical. Using trigonometry:
R=lsin(30∘)=0.2×12=0.1m
- The distance between the two charges (balls) can be found using the geometry of the equilateral triangle formed by the three balls:
d=√3R=√3×0.1=0.1732m
3. Calculate the Forces:
- The gravitational force acting on each ball is:
Fg=mg=10−4×10=10−3N
- The electrostatic force F between any two charges q at a distance d is given by Coulomb's law:
F=kq2d2
- Here, k (Coulomb's constant) is approximately 9×109N m2/C2.
4. Force Balance:
- In the vertical direction, the tension T in the thread balances the weight of the ball:
Tcos(30∘)=mg
- In the horizontal direction, the tension provides the centripetal force due to the electrostatic repulsion:
Tsin(30∘)=F
5. Express Tension:
- From the vertical force balance:
T=mgcos(30∘)=10−3√32=2×10−3√3N
6. Substituting into Horizontal Force Equation:
- Substitute T into the horizontal force equation:
2×10−3√3⋅12=kq2d2
- Simplifying gives:
10−3√3=kq2(0.1732)2
7. Solving for Charge q:
- Rearranging gives:
q2=10−3⋅(0.1732)2k⋅√3
- Plugging in the values:
q2=10−3⋅(0.1732)29×109⋅√3
- Calculating q:
q=√10−3⋅0.03009×109⋅1.732≈3.33×10−8C
Final Answer:
The charge that should be imparted to each ball is approximately q≈3.33×10−8C.
- Convert the mass of each ball from grams to kilograms:
m=0.1g=0.1×10−3kg=10−4kg
- Convert the length of the thread from centimeters to meters:
l=20cm=0.2m
- The angle α=30∘ implies that each ball will be at a distance R from the vertical. Using trigonometry:
R=lsin(30∘)=0.2×12=0.1m
- The distance between the two charges (balls) can be found using the geometry of the equilateral triangle formed by the three balls:
d=√3R=√3×0.1=0.1732m
- The gravitational force acting on each ball is:
Fg=mg=10−4×10=10−3N
- The electrostatic force F between any two charges q at a distance d is given by Coulomb's law:
F=kq2d2
- Here, k (Coulomb's constant) is approximately 9×109N m2/C2.
- In the vertical direction, the tension T in the thread balances the weight of the ball:
Tcos(30∘)=mg
- In the horizontal direction, the tension provides the centripetal force due to the electrostatic repulsion:
Tsin(30∘)=F
- From the vertical force balance:
T=mgcos(30∘)=10−3√32=2×10−3√3N
- Substitute T into the horizontal force equation:
2×10−3√3⋅12=kq2d2
- Simplifying gives:
10−3√3=kq2(0.1732)2
- Rearranging gives:
q2=10−3⋅(0.1732)2k⋅√3
- Plugging in the values:
q2=10−3⋅(0.1732)29×109⋅√3
- Calculating q:
q=√10−3⋅0.03009×109⋅1.732≈3.33×10−8C
The charge that should be imparted to each ball is approximately q≈3.33×10−8C.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A sphere is suspended by a thread of length l. What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
View SolutionTwo small metallic spheres each of mass 'm' are suspended together with strings of length 'l' and placed together. When a quantum of charge 'q' is transferred to each the strings make and angle of 90∘ with each other. The value of 'q' is
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionA particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
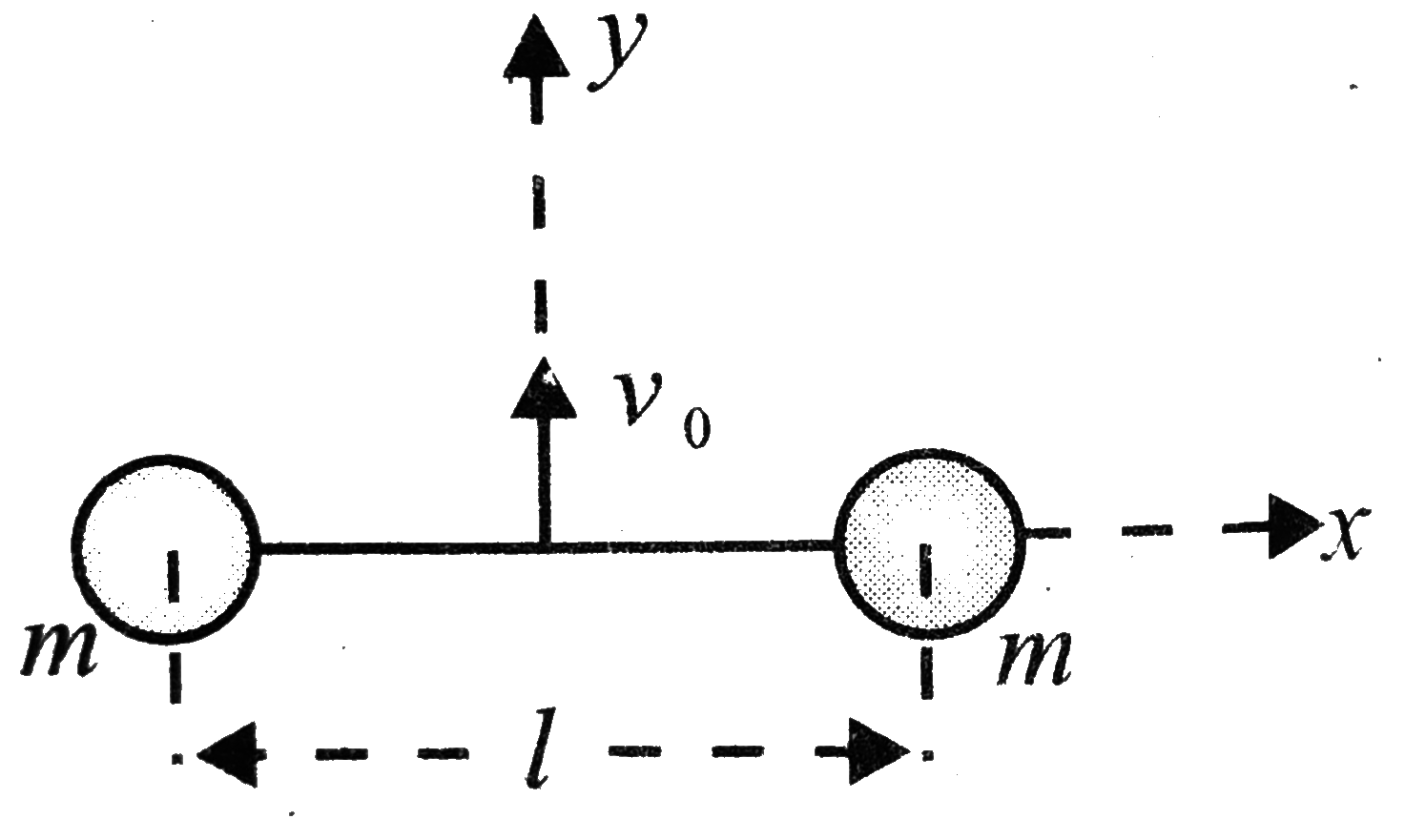
View SolutionTwo identical small balls, each of mass m, are connected by a massless and inextensible string of length l and placed on a smooth horizontal xy plane. An external agent pulling the string from its mid-point along y-axis with velocity v0 as shown in Fig. When the separation between the two balls reduces to l/2 then the speed of each ball will be
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution
