Three immiscible liquids of densities d1>d2>d3 and refractive indices μ1>μ2>μ3 are put in a beaker. The height of each liquid column is h3. A dot is made at the bottom of the beaker. For near normal vision, find the apparent depth of the dot.
h6(1μ1+1μ2+1μ3)
h6(1μ1−1μ2−1μ3)
h3(1μ1−1μ2−1μ3)
h3(1μ1+1μ2+1μ3)
The correct Answer is:D
To find the apparent depth of the dot at the bottom of the beaker containing three immiscible liquids, we can follow these steps:
Step 1: Understand the Setup
We have three immiscible liquids stacked in a beaker, each with a height of h3. The refractive indices of the liquids are given as μ1>μ2>μ3.
Step 2: Define Real Depth
The real depth of the dot at the bottom of the beaker is the total height of the three liquid columns:
Real Depth=h3+h3+h3=h
Step 3: Calculate Apparent Depth for Each Liquid
Using the formula for apparent depth, which relates the real depth and the refractive index:
Apparent Depth=Real Depthμ
For each liquid, we can calculate the apparent depth as follows:
1. For the first liquid (height h3, refractive index μ1):
x1=h3μ1=h3μ1
2. For the second liquid (height h3, refractive index μ2):
x2=h3μ2=h3μ2
3. For the third liquid (height h3, refractive index μ3):
x3=h3μ3=h3μ3
Step 4: Sum the Apparent Depths
The total apparent depth x when viewed from the air through all three liquids is the sum of the individual apparent depths:
x=x1+x2+x3
Substituting the values we calculated:
x=h3μ1+h3μ2+h3μ3
Step 5: Factor Out Common Terms
We can factor out h3 from the expression:
x=h3(1μ1+1μ2+1μ3)
Final Answer
Thus, the apparent depth of the dot is:
x=h3(1μ1+1μ2+1μ3)
We have three immiscible liquids stacked in a beaker, each with a height of h3. The refractive indices of the liquids are given as μ1>μ2>μ3.
The real depth of the dot at the bottom of the beaker is the total height of the three liquid columns:
Real Depth=h3+h3+h3=h
Using the formula for apparent depth, which relates the real depth and the refractive index:
Apparent Depth=Real Depthμ
x1=h3μ1=h3μ1
x2=h3μ2=h3μ2
x3=h3μ3=h3μ3
The total apparent depth x when viewed from the air through all three liquids is the sum of the individual apparent depths:
x=x1+x2+x3
Substituting the values we calculated:
x=h3μ1+h3μ2+h3μ3
We can factor out h3 from the expression:
x=h3(1μ1+1μ2+1μ3)
Thus, the apparent depth of the dot is:
x=h3(1μ1+1μ2+1μ3)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
There are three optical media 1,2 and 3 with the refractive indices μ1>μ2>μ3.
(TIR → total internal reflection)
View SolutionTwo immiscible liquid of densities rho and 3ρ are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats completely inside liquids with its axis vertical and length L3 in the denser liquid. The density d is equal to
View SolutionTwo non-mixing liquids of densities ρ and nρ (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to :
View SolutionThree immiscibles transparent liquids with erefractive indices 3/2,4/3 and 6/5 are arranged one on top of another. The depth of the liquid are 3 cm, 4 cm and 6 cm respectively. The apparent depth of the vessel is
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
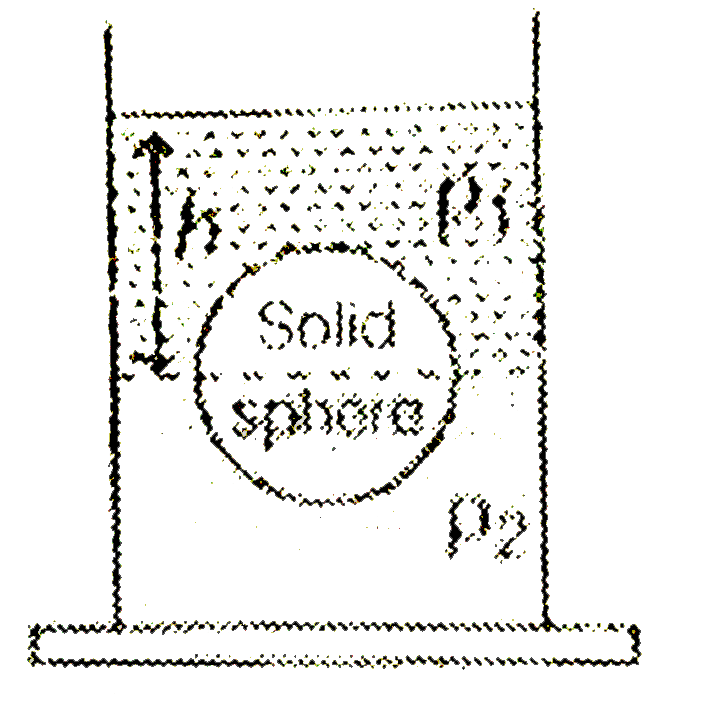
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionIn the figure shown, μ1>μ2>μ3. What are the limits of angle i so that it is neither get total internal reflection at AB nor at CD ?

View SolutionA beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K.oil is mu_2.
View Solution
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities d1 and d2 The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
View Solution
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities d1 and d2 The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
View Solution
