Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

Total thermal resistance
R=R1+R2+R93)=(L1K1A)+L2K2A+L3K3A
Now, Heat transfer H=T1−T2R
∴ H=T1−T2L1K1A+L2K2A+L3K3A
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.1
10 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionThree rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]

View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
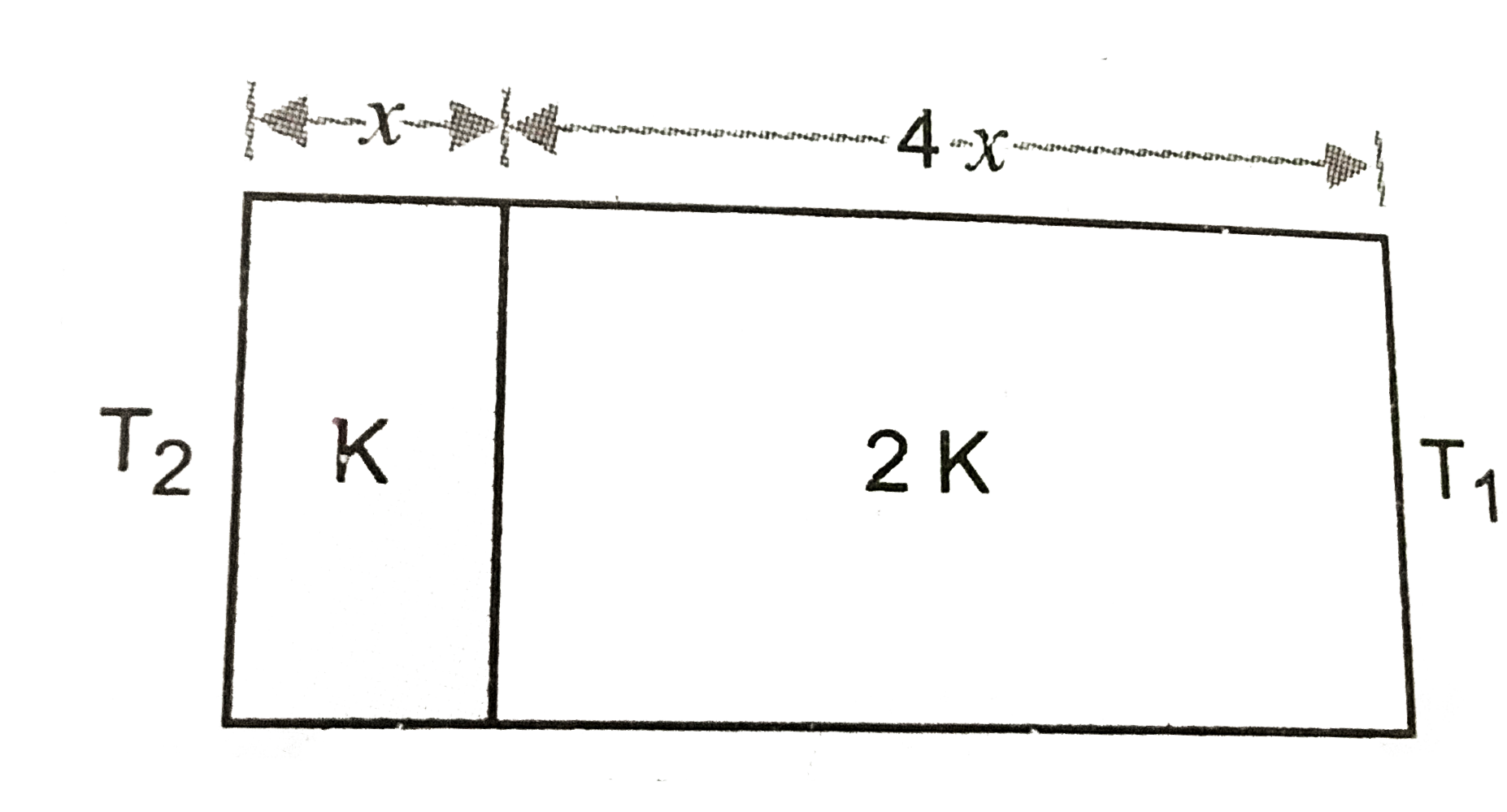 A1B12C23D13
A1B12C23D13
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionTwo identical rods of length (L), area of cross-sectional (A) and thermal conductivity k are joined end to end. If temperature difference of free ends is ΔT, the heat Q0 flows along rods per second. Find the total heat flowing per second along the rods if the two rods are placed parallel and temperature difference of free ends is ΔT. There is no heat loss from curved surface.
View SolutionA hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T2>T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2 .
View SolutionThe temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .
.
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.

If TA and TB are the temperature drops across the rod A and B, then
View Solution
