Two balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
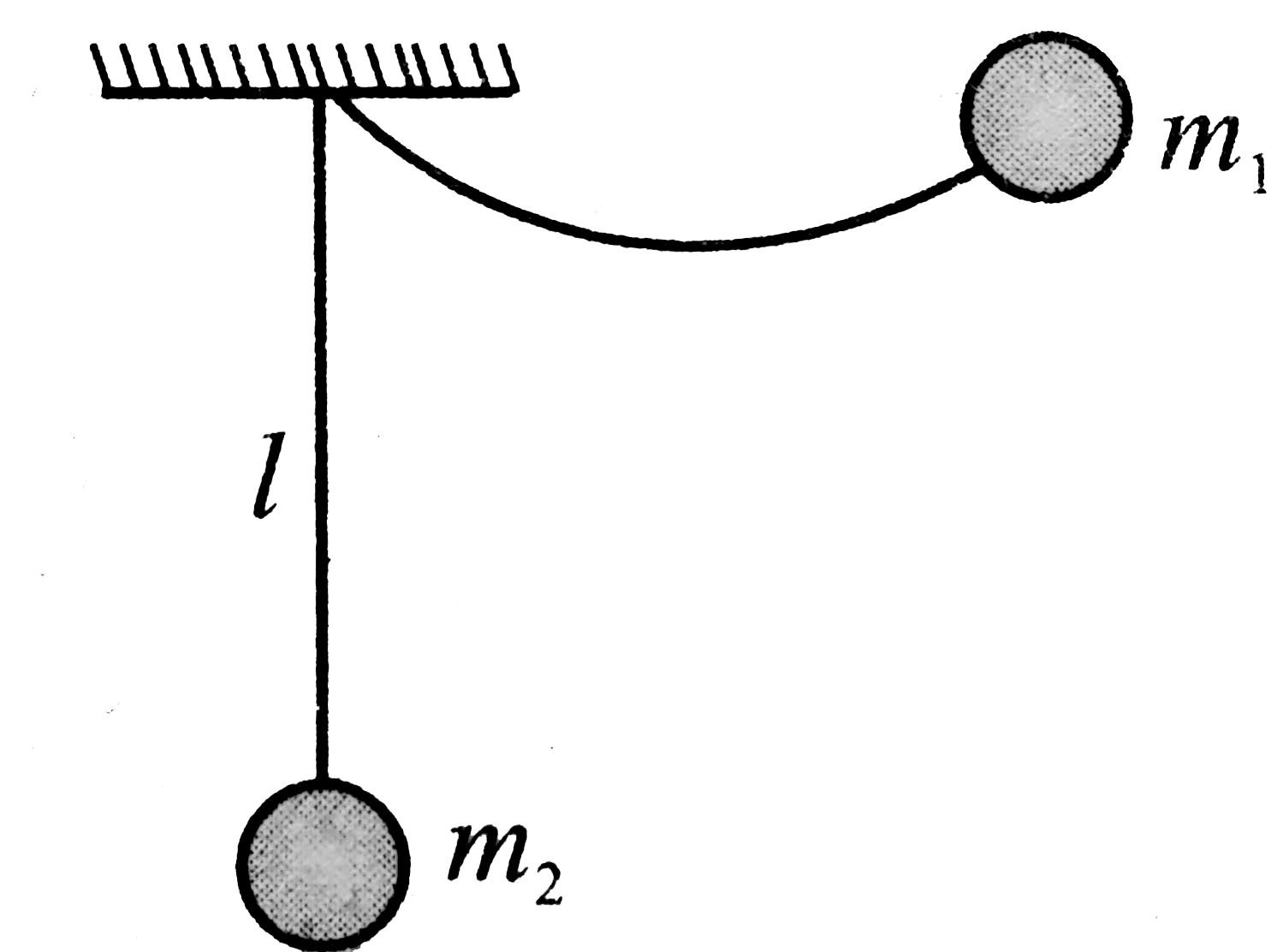 The maximum rise of centre of mass of the ball of mass m2 is
The maximum rise of centre of mass of the ball of mass m2 is
a. 0.20m
b. 0.50m
c. 0.75m
d. 1m
The correct Answer is:A
Ball of mass m1 falls freely till thread becomes taut. At that instant inclination θ of the thread with the vertical be given by
sinθ=(√32l)l=√32 or θ=60∘
Ball of mass m1 falls freely through height.

Velocity of this ball at this instant is v=√2g×l2=√gl
It can be resolved into two components.
i. vcosθ, along the thread. But thread is inextensible, hence this component decreases to zero (due to tension developed in the thread).
ii. vsinθ, perpendicular to the thread. Due to this component ball starts to move along a circle whose centre is at A.
According to law of conservation of energy,
Kinetic energy of ball m1 just before collision = Its kinetic energy at AC+ Further loss of its potential energy
12m1u21=12m1(√glsinθ)2+m1g(l−lcosθ)
u1=4m/s
According to law of conservation of momentums
m1v1+m2v2=m1u1+m2u2
and coefficient of restitution e=v2−v1u2−u1=1
substituting u1=4m/s,u2=,m1=0.1kg and m2=0.3kg,v2=2m/s, the height to which it rises is
h=v222g=0.20m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two balls of masses m1=100g and m2=300g are suspended from point A by two equal inextensible threads, each of length l=3235m. Ball of mass m1 is drawn aside and held at the same level as A but at a distance (√32)l from A, as shown in Fig. When ball m1 is released, it collides elastically with the stationary ball of mass m2.
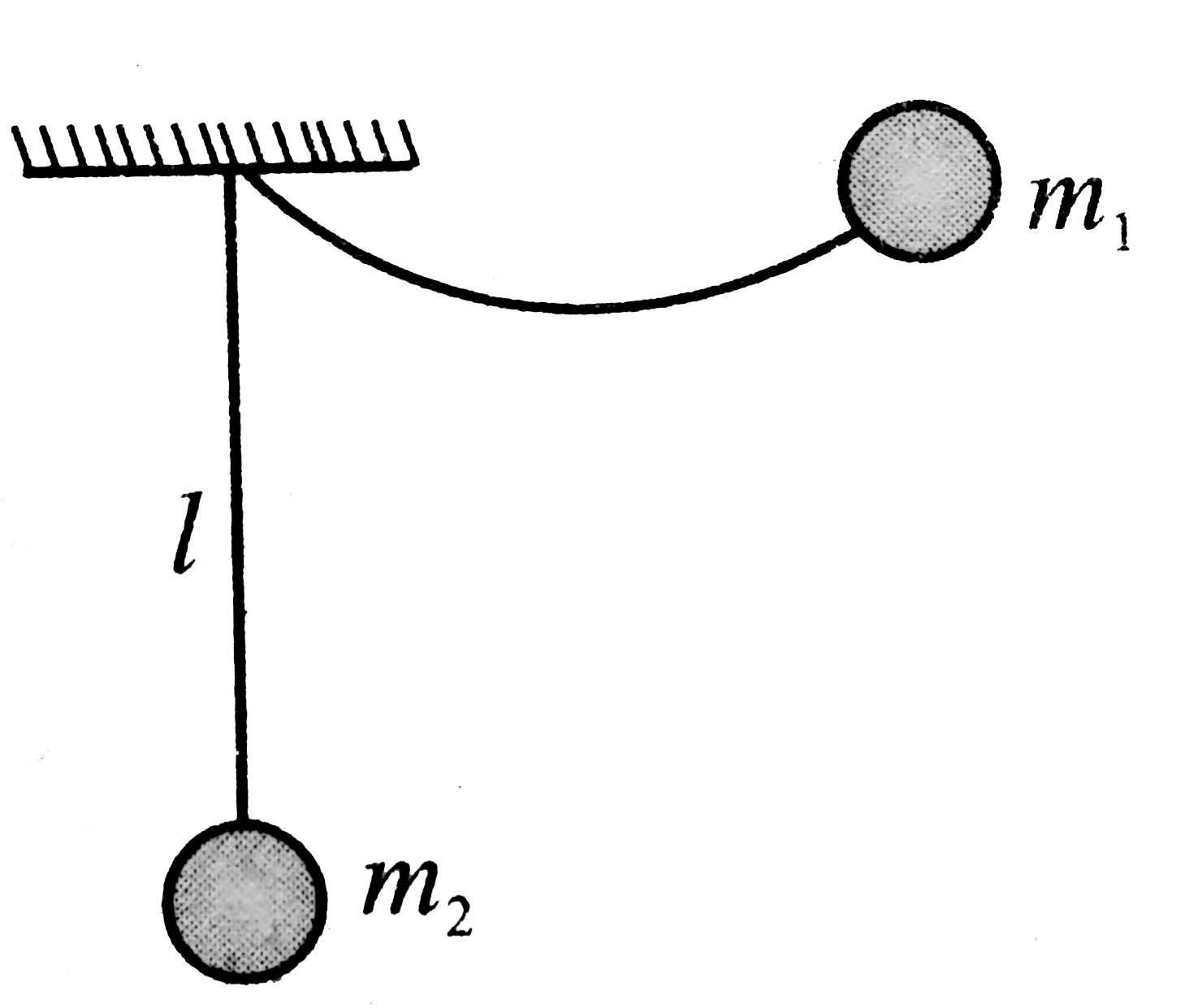
Velocity u1 with which the hall of mass m1 collides with the other ball is
View SolutionA ball of mass m=200gm is suspended from a point A by an inextensible string of length L. Ball is drawn to a side and held at same level as A but at a distance √32L from A as shown. Now the ball is released. Then :( assume string applies only that much jerk which is required so that velocity along string becomes zero ).

View Solution
Knowledge Check
A spherical ball of mass m1 collides head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kinetic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A body of mass M1 collides elastically with another mass M2 at rest. There is maximum transfer of energy when :
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
View SolutionA body of mass m1 collides elastically with a stationary body of mass m2 and returns along the same line with one fourth of its initial speed, then m1/m2=
View SolutionA ball of mass m1 is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m2 . The velocity of both the balls become v after collision. Then the value of the ratio m2m1 is
View SolutionA ball of mass m collides with a stationary identical ball a speed v0. Find the impulse of the colliding balls (e=1/2).
View Solution
