Two blocks are connected to an ideal spring of stiffness 200N/m. At a certain moment, the two block are moving in opposite diretion with speeds 4ms1 and ' 6 ms_(1) ' the instantaneous elongation of the spring 10cm, The rate at which the spring energy ((kx22) is increasing is: a) 500 J/s b) 400 J/s c) 200 J/s d) 100 J/s
500J/s
400J/s
200J/s
100J/s.
The correct Answer is:C
To solve the problem, we need to find the rate at which the spring energy is increasing when two blocks are connected to an ideal spring. The spring's stiffness is given as k=200N/m, the elongation of the spring is x=10cm=0.1m, and the speeds of the two blocks are v1=4m/s and v2=6m/s.
1. Understanding the Energy in the Spring:
The potential energy stored in the spring is given by the formula:
U=12kx2
where U is the potential energy, k is the spring constant, and x is the elongation of the spring.
2. Calculating the Potential Energy:
Plugging in the values:
U=12×200N/m×(0.1m)2=12×200×0.01=1J
3. Finding the Rate of Change of Potential Energy:
The rate at which the potential energy is increasing can be found using the relationship between the change in potential energy and the change in kinetic energy of the blocks. The increase in potential energy per unit time is equal to the decrease in kinetic energy of both blocks.
4. Calculating Kinetic Energy of Each Block:
The kinetic energy of each block is given by:
KE=12mv2
Since we do not have the masses of the blocks, we will denote the mass of the first block as m1 and the second block as m2.
5. Finding the Rate of Change of Kinetic Energy:
The rate of change of kinetic energy for each block is:
d(KE1)dt=12m1d(v21)dt=m1v1dv1dt
d(KE2)dt=12m2d(v22)dt=m2v2dv2dt
6. Using Newton's Second Law:
According to Newton's second law, the force exerted by the spring on each block is:
F=kx
Therefore, the force on each block is equal to the spring force:
F1=−kxandF2=kx
7. Setting Up the Equation:
The increase in potential energy per unit time is equal to the decrease in kinetic energy:
dUdt=−(d(KE1)dt+d(KE2)dt)
We can express this in terms of the velocities and spring force.
8. Calculating the Rate of Change of Spring Energy:
The rate at which the spring energy is increasing is given by:
dUdt=kx(v1+v2)
Substituting the values:
dUdt=200N/m×0.1m×(4m/s+6m/s)=200×0.1×10=200J/s
9. Final Answer:
The rate at which the spring energy is increasing is 200J/s.
Conclusion:
The correct answer is option c) 200 J/s.
The potential energy stored in the spring is given by the formula:
U=12kx2
where U is the potential energy, k is the spring constant, and x is the elongation of the spring.
Plugging in the values:
U=12×200N/m×(0.1m)2=12×200×0.01=1J
The rate at which the potential energy is increasing can be found using the relationship between the change in potential energy and the change in kinetic energy of the blocks. The increase in potential energy per unit time is equal to the decrease in kinetic energy of both blocks.
The kinetic energy of each block is given by:
KE=12mv2
Since we do not have the masses of the blocks, we will denote the mass of the first block as m1 and the second block as m2.
The rate of change of kinetic energy for each block is:
d(KE1)dt=12m1d(v21)dt=m1v1dv1dt
d(KE2)dt=12m2d(v22)dt=m2v2dv2dt
According to Newton's second law, the force exerted by the spring on each block is:
F=kx
Therefore, the force on each block is equal to the spring force:
F1=−kxandF2=kx
The increase in potential energy per unit time is equal to the decrease in kinetic energy:
dUdt=−(d(KE1)dt+d(KE2)dt)
We can express this in terms of the velocities and spring force.
The rate at which the spring energy is increasing is given by:
dUdt=kx(v1+v2)
Substituting the values:
dUdt=200N/m×0.1m×(4m/s+6m/s)=200×0.1×10=200J/s
The rate at which the spring energy is increasing is 200J/s.
The correct answer is option c) 200 J/s.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective
15 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Two identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V0 maximum extension of spring is
View SolutionFree end of an ideal spring of spring constant 100 N/m is at a distance 1 m from a vertical block of mass 2 kg moving on rough surface with initial speed 8 m/s as shown in figure. If coefficient of friction is 0.7, then maximum compression in spring is (g=10ms−2)
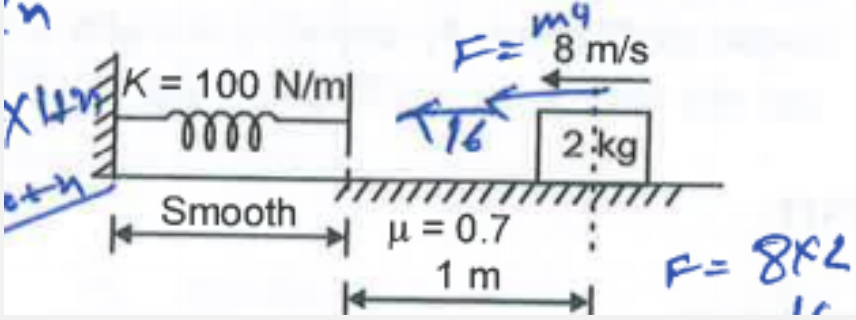
View Solution
Knowledge Check
An solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is: a) 40 J s b) 400 J s c) 20 J s d) 200 J s
A40 J sB400 J sC20 J sD200 J s
Two blocks A and B are joined together with a compressed spring. When the system is released, the two bloks appear to be moving with unequal speeds in the opposite directions as shown in figure.
Select incorrect statements(s) :
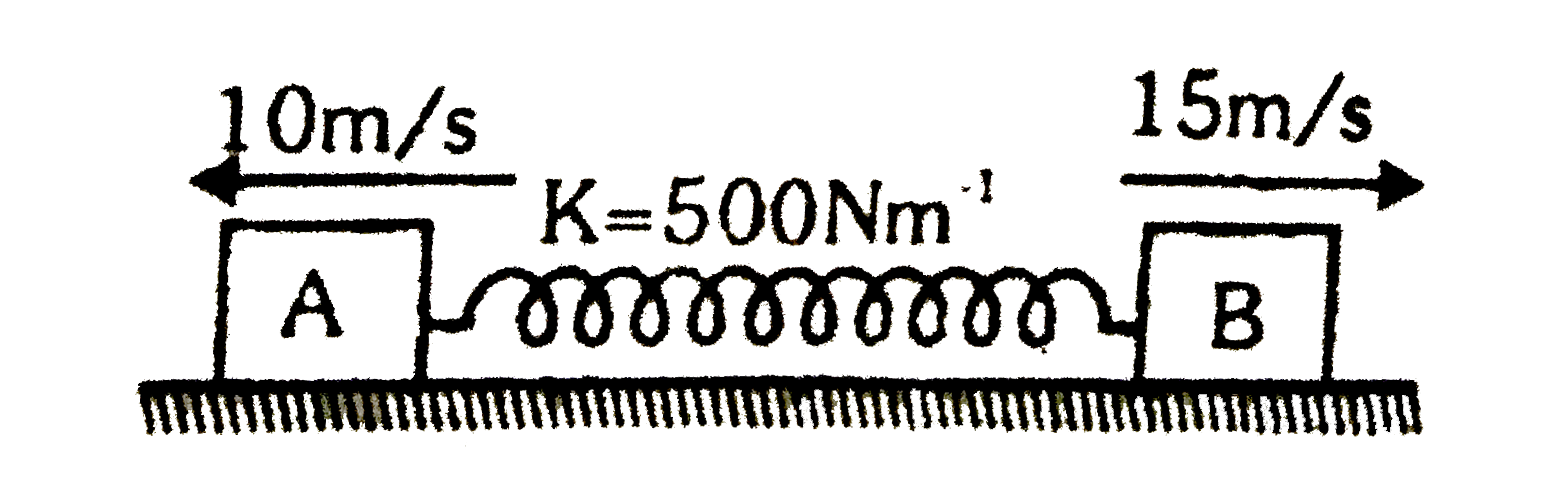
View SolutionTwo blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shape impulse so that it acquires a velocity v0 towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.
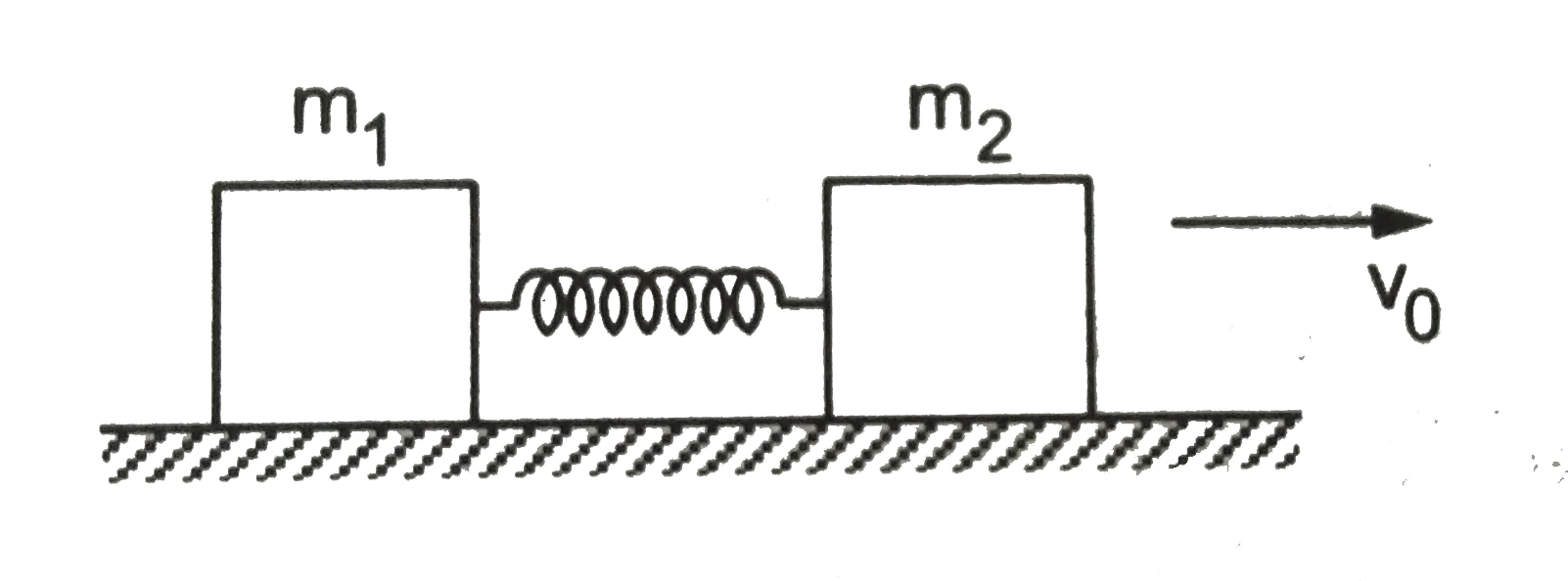
View SolutionTwo blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
View SolutionA block of mass M is placed on a smooth horizontal surface and it is pulled by a light spring as shown in the diagram. If the ends A and B of the spring are moving with 4ms−2and2ms−1 respectively and the rate at which spring energy is increasing is 20Js−1. then what is the value of spring force (in N)?
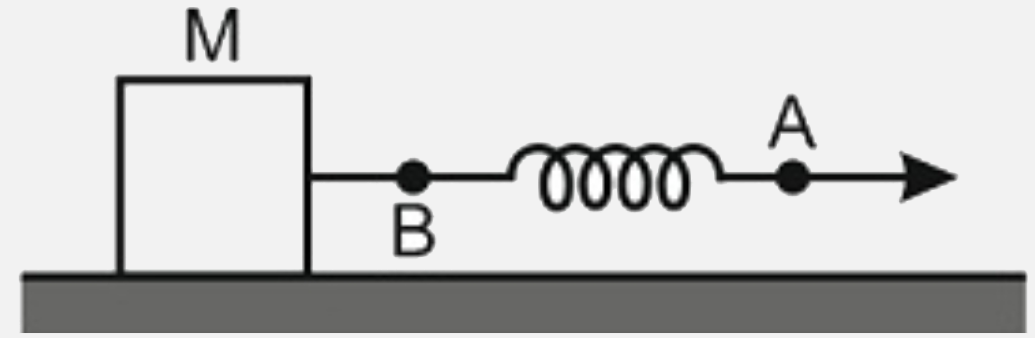
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring contant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .

View Solution