Two blocks of unequal masses are tied by a spring. The blocks are pulled stretching the spring slightly and the system is released on a frictionless horizontal platform. Are the forces due to the spring on the two blocks equal and opposite. If yes, is it can example of Newton's third law?
To solve the problem, we need to analyze the forces acting on the two blocks connected by a spring when they are pulled and then released on a frictionless surface.
1. Identify the System:
We have two blocks of unequal masses, let's denote them as m1 and m2, connected by a spring with spring constant k.
2. Understanding the Spring Force:
When the blocks are pulled apart, the spring stretches, creating a restoring force. According to Hooke's Law, the force exerted by the spring is proportional to the displacement x from its equilibrium position:
F=kx
This force acts on both blocks.
3. Force on Each Block:
- The force exerted by the spring on block m1 is Fs1=kx (acting towards m2).
- The force exerted by the spring on block m2 is Fs2=−kx (acting towards m1).
Here, the negative sign indicates that the force on m2 is in the opposite direction to that on m1.
4. Equal and Opposite Forces:
According to Newton's Third Law, for every action, there is an equal and opposite reaction. Therefore, the forces due to the spring on the two blocks are equal in magnitude but opposite in direction:
Fs1=−Fs2
Thus, the forces are indeed equal and opposite.
5. Application of Newton's Third Law:
Although we have established that the forces are equal and opposite, we need to clarify whether this situation exemplifies Newton's Third Law. The law states that the action and reaction forces must act on two different bodies. In this case:
- The force exerted by the spring on block m1 and the force exerted by block m1 on the spring are an action-reaction pair.
- Similarly, the force exerted by the spring on block m2 and the force exerted by block m2 on the spring is another action-reaction pair.
However, since we are considering the system of two blocks and the spring as a whole, the interaction between the two blocks through the spring does not represent a direct application of Newton's Third Law between just the blocks. Therefore, while the forces are equal and opposite, the situation as a whole does not serve as a classic example of Newton's Third Law.
Conclusion:
Yes, the forces due to the spring on the two blocks are equal and opposite. However, this situation is not a direct example of Newton's Third Law when considering the system as a whole.
We have two blocks of unequal masses, let's denote them as m1 and m2, connected by a spring with spring constant k.
When the blocks are pulled apart, the spring stretches, creating a restoring force. According to Hooke's Law, the force exerted by the spring is proportional to the displacement x from its equilibrium position:
F=kx
This force acts on both blocks.
- The force exerted by the spring on block m1 is Fs1=kx (acting towards m2).
- The force exerted by the spring on block m2 is Fs2=−kx (acting towards m1).
Here, the negative sign indicates that the force on m2 is in the opposite direction to that on m1.
According to Newton's Third Law, for every action, there is an equal and opposite reaction. Therefore, the forces due to the spring on the two blocks are equal in magnitude but opposite in direction:
Fs1=−Fs2
Thus, the forces are indeed equal and opposite.
Although we have established that the forces are equal and opposite, we need to clarify whether this situation exemplifies Newton's Third Law. The law states that the action and reaction forces must act on two different bodies. In this case:
- The force exerted by the spring on block m1 and the force exerted by block m1 on the spring are an action-reaction pair.
- Similarly, the force exerted by the spring on block m2 and the force exerted by block m2 on the spring is another action-reaction pair.
Yes, the forces due to the spring on the two blocks are equal and opposite. However, this situation is not a direct example of Newton's Third Law when considering the system as a whole.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises42videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
Two blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

Then the displacement of the centre of mass in at time t isView SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isView SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isView SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure. (a) Find the displacement of the centre of mass at time t. (b) If the extension of the spring is x0 at time t, find the displacement of the two blocks at this instant.
 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.View SolutionTwo springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
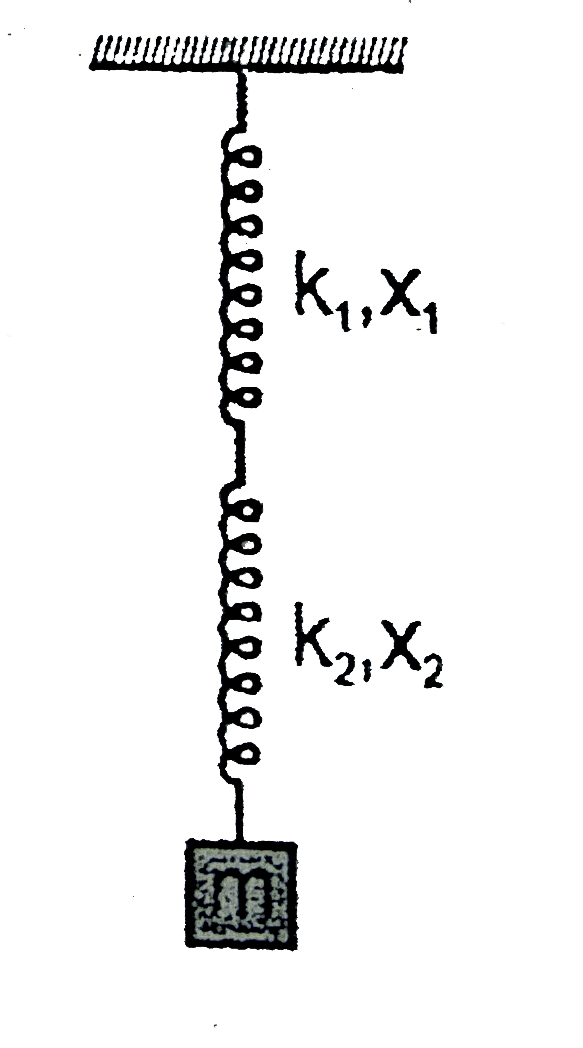 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of springView Solution

