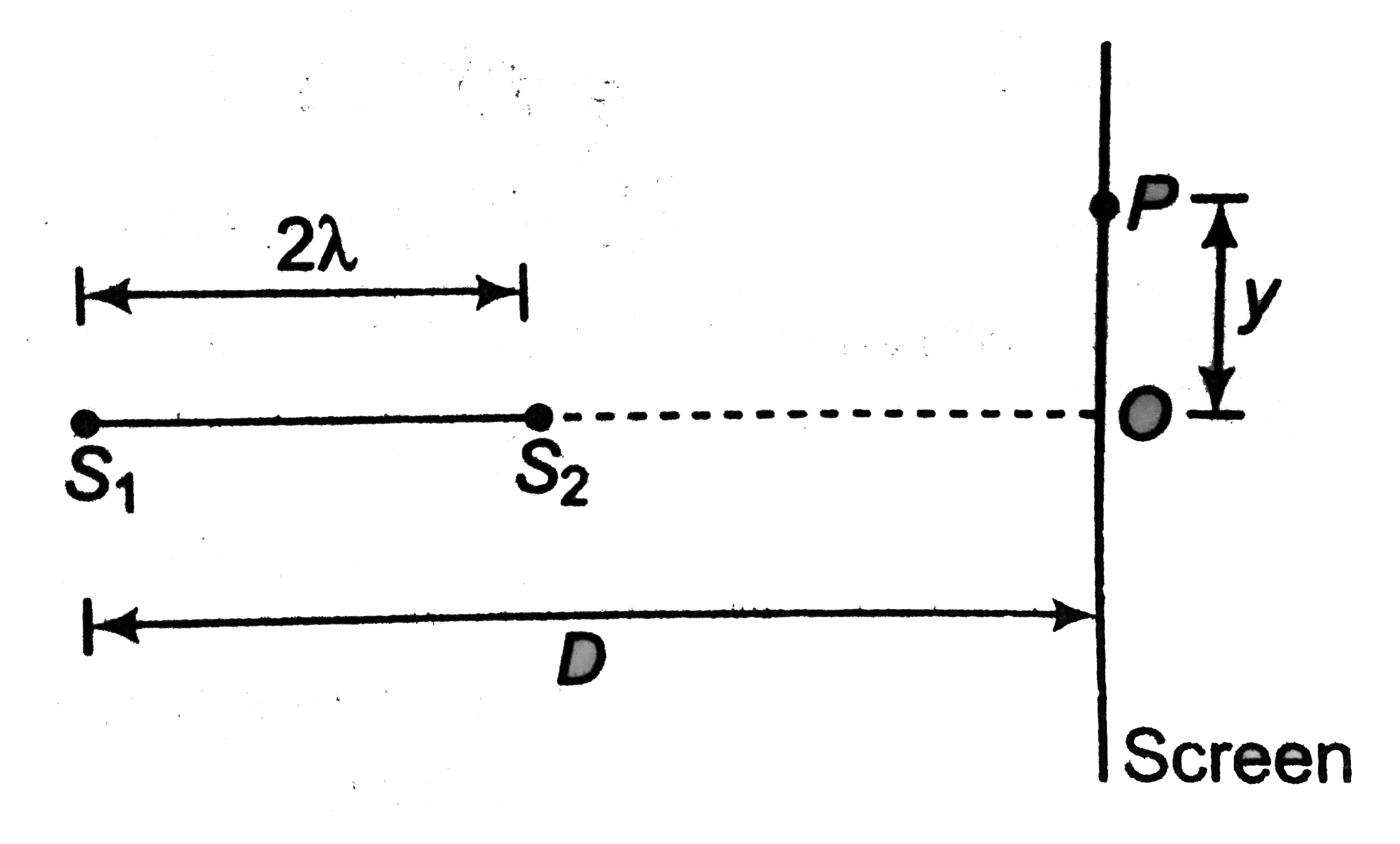
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
 Solution in Tamil
Solution in Tamil
The correct Answer is:C, D
Since S1,S2 are in same phase at O there wil be maximum intensity.
Given that there will be a maximum intensity at P.
→pathd⇔erence=△x=nl

From the ure (in question)
(S1P)2−(S2P)2
=(sqrtD^2+x_2)^2-[(sqrtD-2lamda^2+x^2]^2<br>=4lamdaD=4lamda^2=4lamdaD<br>(lamda^2issosmallandcan²cted)<br>S_1P-S_2P=(4lamdaD)/(2sqrt(x^2+D^2))=nlamda<br>=(2D)/(sqrt(x^2+D^2))=n<br>rarr n^2(x^2+D^2)=4D^2<br>rarr x=D/n sqrt4-n^2<br>Whenn=1, x=sqrt3D(1st order)<br>n=2,<br>x=0 (2nd order)
∴Wenx=√3D
at P there will be maximum intensity
Topper's Solved these Questions
Similar Questions
A load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View Solution0.32g of oxygen is kept in a rigid container and is heated. Find the amount of heat needed to raise the temperature from 250C→350C. The molar heat capacity of oxygen at constant volume is 20JK−1mol−1.
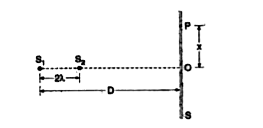
06:11View SolutionTwo coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2lamda . The sound is detected by moving a detector on the screen sum at a distance D(gtgtlamda) from the slit S_1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
04:00View SolutionTwo coherent narrow slits emitting wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda , the sound is detected by moving a detector on the screen S at a distance D (gtgt lambda) from the slit S_(1) as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O .
03:33View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
05:22View SolutionTwo coherent narrow slits emitting light of wavelength lamda in the same phase are placed parallel to each other at a small separation of 3lamda the light is collected on a screen S which is placed at a distance D(gt gt lamda) from the slits the smallest distance x such that the P is a maxima.
04:20View SolutionTwo coherent point sources S_1 and S_2 vibrating in phase emit light of wavelength lamda . The separation between them is 2lamda . The light is collected on a screen placed at a distance Dgt gt lamda from the slit S_1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
05:23View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......
02:46View SolutionTwo coherant narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda .The light is collected on a screen S which is placed at a distance D( gt gt A) from the slit S_(1) as shown in figure .Find teh finite distance x such that the intensity of P is equal to intensity at O .
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
02:05View SolutionThe intensity at the maximum in a Young's double slit experiment is I_(0) . Distance between two slits is d=5 lambda , where lambda is the wavelength of light used in the experiment. The intensity infront of one of the slits on the screen placed at a distance D=10 d is (I_(0))/(n) . Find n .
04:24View Solution_S01_032_Q01.png)
Figure shows two coherent microwave source S1 and S2 emitting waves of wavelength λ and separated by a distance 3λ for λ<<D and y≠0. The minimum value of y for point P to be an intensity maximum is √mDn determine the value of m+n, if m and n are coprime numbers.View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
05:52View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(>>λ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity at O.
 03:53View Solution
03:53View Solution

