Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.

Text Solution

Verified by Experts

(i) Let there be two concentric circular coils of radii r and R respectively. Where R $> >$ r. If a current $I_{1}$ , flows through the outer coil, then magnetic field developed at its centre is
$B = \frac{μ_{0} I_{1}}{2 R}$
As r is very small, magnetic field on the inner loop may be assumed to be uniform at
$B = \frac{μ_{0} I_{1}}{2 R}$
$∴$ Magnetic flux linked with inner loop $ϕ_{2} = B (π r^{2}) = \frac{μ_{0} I_{1} π r^{2}}{2 R}$
$∵ ϕ_{2} = M I_{1}$

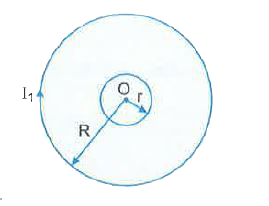
$∴$ Mutual inductance of the given pair of coils M= $\frac{ϕ_{2}}{I_{1}} = \frac{μ_{0} π r^{2}}{2 R}$
As per question R =20 cm = 0.2 m and r =1 cm = 0.01 m
$∴ M = \frac{(4 π \times 10^{- 7}) \times π \times {(0.01)}^{2}}{2 \times 0.2} = 9.87 \times 10^{10}$ H
(ii) If rate of change of current in outer loop i.e., $\frac{d I_{1}}{d t} = 5 A / m s = 5 \times 10^{3} A s^{- 1}$ then magnitude of induced emf in the inner loop is
$ε_{2} = M \frac{d I_{1}}{d t} = (9.87 \times 10^{- 10}) \times (5 \times 10^{- 3}) = 4.935 \times 10^{- 6} V = 4.9 μ V$

Updated on:21/07/2023

|

Class 12 PHYSICS CBSE EXAMINATION PAPER 2020 (SOLVED)

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two different wire loops are concentric and lie in the same plane. The current in the outer loop is clockwise and increasing with time. The induced current in the inner loop then is
Aclockwise
Bzero
Ccounter clockwise
Din a direction that depends on the ratio of the, loop radii

U-LIKE SERIES-CBSE EXAMINATION PAPER 2020 (SOLVED)-SECTION D

Home
Ask Doubt
Profile