Two condensers of capacity 0.3μF and 0.6μF respectively are connected in series. The combination is connected across a potential of 6 volts. The ratio of energies stored by the condensers will be
12
2
14
4
The correct Answer is:B
To find the ratio of energies stored by two capacitors connected in series, we can follow these steps:
Step 1: Understand the Capacitors in Series
When capacitors are connected in series, they have the same charge (Q) on them. The total voltage (V) across the series combination is the sum of the voltages across each capacitor.
Step 2: Calculate the Equivalent Capacitance
The formula for the equivalent capacitance (C_eq) of capacitors in series is given by:
1Ceq=1C1+1C2
Where:
- C1=0.3μF
- C2=0.6μF
Substituting the values:
1Ceq=10.3+10.6
Step 3: Calculate the Individual Contributions
Calculating the right-hand side:
1Ceq=20.6+10.6=30.6=5
Thus,
Ceq=15=0.2μF
Step 4: Calculate the Charge (Q)
The total charge (Q) stored in the capacitors can be calculated using the formula:
Q=Ceq×V
Where V=6V:
Q=0.2μF×6V=1.2μC
Step 5: Calculate the Energy Stored in Each Capacitor
The energy (U) stored in a capacitor is given by the formula:
U=Q22C
For Capacitor 1 (C1 = 0.3 μF):
U1=Q22C1=(1.2×10−6)22×0.3×10−6=1.44×10−120.6×10−6=2.4×10−6J
For Capacitor 2 (C2 = 0.6 μF):
U2=Q22C2=(1.2×10−6)22×0.6×10−6=1.44×10−121.2×10−6=1.2×10−6J
Step 6: Find the Ratio of Energies
Now, we can find the ratio of the energies stored in the two capacitors:
U1U2=2.4×10−61.2×10−6=2
Final Answer
The ratio of energies stored by the capacitors is 2:1.
---
When capacitors are connected in series, they have the same charge (Q) on them. The total voltage (V) across the series combination is the sum of the voltages across each capacitor.
The formula for the equivalent capacitance (C_eq) of capacitors in series is given by:
1Ceq=1C1+1C2
Where:
- C1=0.3μF
- C2=0.6μF
1Ceq=10.3+10.6
Calculating the right-hand side:
1Ceq=20.6+10.6=30.6=5
Thus,
Ceq=15=0.2μF
The total charge (Q) stored in the capacitors can be calculated using the formula:
Q=Ceq×V
Where V=6V:
Q=0.2μF×6V=1.2μC
The energy (U) stored in a capacitor is given by the formula:
U=Q22C
U1=Q22C1=(1.2×10−6)22×0.3×10−6=1.44×10−120.6×10−6=2.4×10−6J
U2=Q22C2=(1.2×10−6)22×0.6×10−6=1.44×10−121.2×10−6=1.2×10−6J
Now, we can find the ratio of the energies stored in the two capacitors:
U1U2=2.4×10−61.2×10−6=2
The ratio of energies stored by the capacitors is 2:1.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
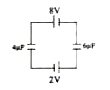
Two condensers of capacities 4mF and 6mF are connected to two cells as shown. Then
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power supplied by the battery,
View Solution
Knowledge Check
Two capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
A2 VB8 VC6 VD1 V
Two resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.
View SolutionA condenser of capacity 1 μ F and a resistance 0.5 mega-ohm are connected in series with a DC supply of 2 V. The time constant of circuit is
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is

View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionTwo capicitors of capacitances 4and6μF respectively are connected in series across a pd of 250 V. These are disconnected and now connected in parallel. Find the new pd and charge on each capacitor.
View Solution
