Two identical short bar magnets, each having magnetic moment M, are placed a distance of 2d apart with axes perpendicular to each other in a horizontal plane. The magnetic induction at a point midway between them is
μ04π(√2)Md3
μ04π(√3)Md3
(2μ04π)Md3
μ04π(√5)Md3
The correct Answer is:D
To find the magnetic induction at a point midway between two identical short bar magnets, each having a magnetic moment M and placed a distance of 2d apart with their axes perpendicular to each other, we can follow these steps:
Step 1: Understand the Configuration
We have two bar magnets positioned such that their centers are 2d apart. The axes of the magnets are perpendicular to each other. The point of interest (point P) is located midway between the two magnets, which means it is at a distance d from each magnet.
Step 2: Determine the Magnetic Field Due to Each Magnet
For a bar magnet, the magnetic induction (magnetic field) at a point along the axial line (the line extending from the north to the south pole) is given by the formula:
B1=2Mμ0πd3
where B1 is the magnetic induction due to the first magnet, M is the magnetic moment, μ0 is the permeability of free space, and d is the distance from the magnet.
For the second magnet, which is positioned perpendicular to the first, the magnetic field at point P (which is at a distance d) is given by the formula for the equatorial point:
B2=Mμ04πd3
Step 3: Calculate the Magnetic Fields
1. Magnetic Field from the First Magnet (Axial):
B1=2Mμ0πd3
2. Magnetic Field from the Second Magnet (Equatorial):
B2=Mμ04πd3
Step 4: Determine the Direction of the Magnetic Fields
- The magnetic field B1 from the first magnet will be directed along the axis of the magnet.
- The magnetic field B2 from the second magnet will be directed perpendicular to B1.
Step 5: Calculate the Resultant Magnetic Field
Since B1 and B2 are perpendicular to each other, we can find the net magnetic field B at point P using the Pythagorean theorem:
B=√B21+B22
Substituting the values of B1 and B2:
B=√(2Mμ0πd3)2+(Mμ04πd3)2
Step 6: Simplify the Expression
Calculating B:
B=√4M2μ20π2d6+M2μ2016π2d6
Factoring out common terms:
B=√M2μ20π2d6(4+116)
Calculating the term in the parentheses:
4+116=6416+116=6516
Thus,
B=√M2μ20π2d6⋅6516=Mμ0πd3⋅√6516=Mμ04πd3√65
Final Answer
The magnetic induction at the point midway between the two magnets is:
B=Mμ0√654πd3
We have two bar magnets positioned such that their centers are 2d apart. The axes of the magnets are perpendicular to each other. The point of interest (point P) is located midway between the two magnets, which means it is at a distance d from each magnet.
For a bar magnet, the magnetic induction (magnetic field) at a point along the axial line (the line extending from the north to the south pole) is given by the formula:
B1=2Mμ0πd3
where B1 is the magnetic induction due to the first magnet, M is the magnetic moment, μ0 is the permeability of free space, and d is the distance from the magnet.
B2=Mμ04πd3
1. Magnetic Field from the First Magnet (Axial):
B1=2Mμ0πd3
B2=Mμ04πd3
- The magnetic field B1 from the first magnet will be directed along the axis of the magnet.
- The magnetic field B2 from the second magnet will be directed perpendicular to B1.
Since B1 and B2 are perpendicular to each other, we can find the net magnetic field B at point P using the Pythagorean theorem:
B=√B21+B22
B=√(2Mμ0πd3)2+(Mμ04πd3)2
Calculating B:
B=√4M2μ20π2d6+M2μ2016π2d6
Factoring out common terms:
B=√M2μ20π2d6(4+116)
Calculating the term in the parentheses:
4+116=6416+116=6516
Thus,
B=√M2μ20π2d6⋅6516=Mμ0πd3⋅√6516=Mμ04πd3√65
The magnetic induction at the point midway between the two magnets is:
B=Mμ0√654πd3
Similar Questions
Two identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View SolutionTwo identical magnetic dipoles of magnetic moments 1⋅0Am2 each are placed at a separation of 2m with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
View Solution
Knowledge Check
- Question 1 - Select One
Two identical magnetic dipoles of magnetic moments 1⋅0Am2 each are placed at a separation of 2m with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
A√5×10−7TB5×10−7TC√2×10−7TD10−7T - Question 2 - Select One
Two identical magnetic dipoles of magnetic moments 2Am2 are placed at a separation of 2m with their axes perpendicular to each other in air. The resultant magnetic field at a mid point between the dipole is
A4√5×10−5 TB2√5×10−5 TC4√5×10−7 TD2√5×10−7 T
Figure shows two identical magnetic dipoles aandb of magnetic moments M each, placed at a separation d, with their axes perpendicular to each other. Find the magnetic field at the point P midway between the dipoles.
 View Solution
View SolutionTwo identical short bar magnets of magnetic moment M each are placed at distance r apart in end-on position, then magnetic force between both is
View SolutionTwo long straight parallel conductors 10 cm apart, carry currents of 5A each in the same direction. Then the magnetic induction at a point midway between them is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo magnets, each of magnetic miment 'M' are placed so as to form a cross at right angles to each other. The magnetic moment of the system will be
View SolutionThree semi - inifinte wires, each carrying a current of 1 A are placed on each of the coordinate axes with their ends at the origin, as shown in the figure. The magnetic induction at point P(−2m,0,0) is
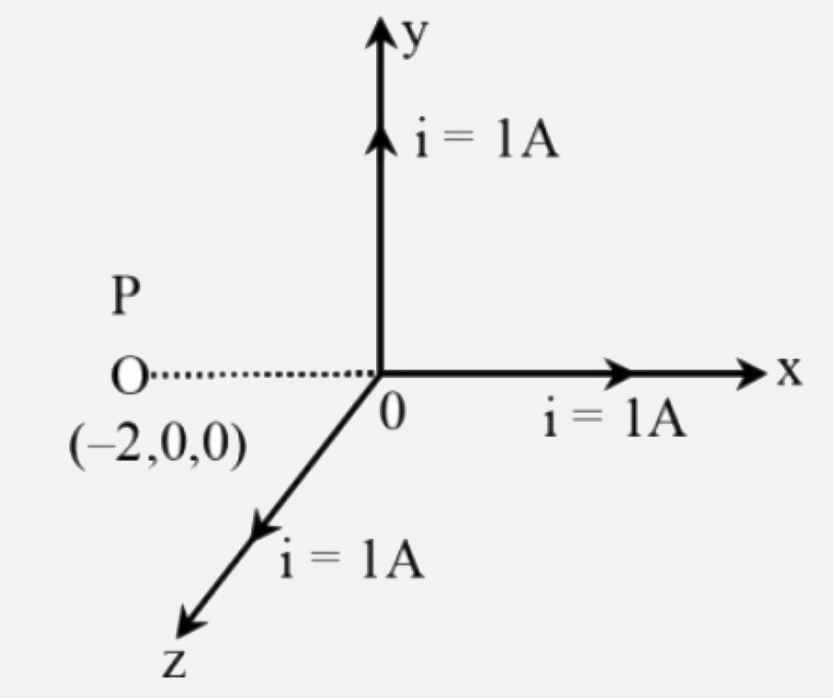 View Solution
View Solution

