Two identical thin rings each of radius R are coaxially placed at a distance R. If the rings have a uniform mass distribution and each has masses 2m and 4m respectively, then the work done in moving a mass m from centre of one ring to that of the other is
zero
√2Gm2R(1−√2)
Gm2√2R(√2−1)
Gm2√2R
The correct Answer is:B
To solve the problem of finding the work done in moving a mass m from the center of one ring to that of the other, we will follow these steps:
Step 1: Understand the potential due to a ring
The gravitational potential V at a point along the axis of a ring of mass M and radius R at a distance z from the center of the ring is given by the formula:
V=−GM√R2+z2
where G is the gravitational constant.
Step 2: Calculate the potential at the center of the first ring
For the first ring with mass 2m located at the origin (let's say z=0), the potential at its center (where z=0) is:
V1=−G(2m)√R2+02=−2GmR
Step 3: Calculate the potential at the center of the second ring
The second ring with mass 4m is located at a distance R along the axis (so z=R). The potential at the center of the second ring is:
V2=−G(4m)√R2+R2=−4Gm√2R=−4GmR√2
Step 4: Calculate the change in potential energy
The work done W in moving the mass m from the center of the first ring to the center of the second ring is equal to the change in potential energy:
W=m(V2−V1)
Substituting the values of V1 and V2:
W=m(−4GmR√2−(−2GmR))
W=m(−4GmR√2+2GmR)
Step 5: Simplify the expression
Now, factor out GmR:
W=GmR(−4m√2+2m)
To combine the terms, we can express 2m in terms of √2:
2m=2m√2√2=2√2m√2
Thus,
W=GmR(−4m√2+2√2m√2)
W=GmR(−4m+2√2m√2)
Step 6: Final expression for work done
Now, we can simplify this further:
W=GmR√2(−4m+2√2m)
This gives us the final expression for the work done in moving the mass m from the center of one ring to the center of the other.
Final Answer
The work done in moving the mass m from the center of one ring to that of the other is:
W=GmR√2(2√2m−4m)
The gravitational potential V at a point along the axis of a ring of mass M and radius R at a distance z from the center of the ring is given by the formula:
V=−GM√R2+z2
where G is the gravitational constant.
For the first ring with mass 2m located at the origin (let's say z=0), the potential at its center (where z=0) is:
V1=−G(2m)√R2+02=−2GmR
The second ring with mass 4m is located at a distance R along the axis (so z=R). The potential at the center of the second ring is:
V2=−G(4m)√R2+R2=−4Gm√2R=−4GmR√2
The work done W in moving the mass m from the center of the first ring to the center of the second ring is equal to the change in potential energy:
W=m(V2−V1)
Substituting the values of V1 and V2:
W=m(−4GmR√2−(−2GmR))
W=m(−4GmR√2+2GmR)
Now, factor out GmR:
W=GmR(−4m√2+2m)
To combine the terms, we can express 2m in terms of √2:
2m=2m√2√2=2√2m√2
Thus,
W=GmR(−4m√2+2√2m√2)
W=GmR(−4m+2√2m√2)
Now, we can simplify this further:
W=GmR√2(−4m+2√2m)
This gives us the final expression for the work done in moving the mass m from the center of one ring to the center of the other.
The work done in moving the mass m from the center of one ring to that of the other is:
W=GmR√2(2√2m−4m)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Two identical thin ring each of radius R are co-axially placed at a distance R. If the ring have a uniform mass distribution and each has mass m1 and m2 respectively, then the work done in moving a mass m from the centre of one ring to that of the other is :
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View Solution
Knowledge Check
Two identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
Two identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
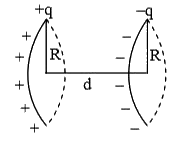
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionTwo identicaln thin rings each of radius 10 cm carrying charges 10 C and 5 C are coaxially placed at a distance 10 cm apart. The work done in moving a charge q from the centre of the first ring to that of the second is
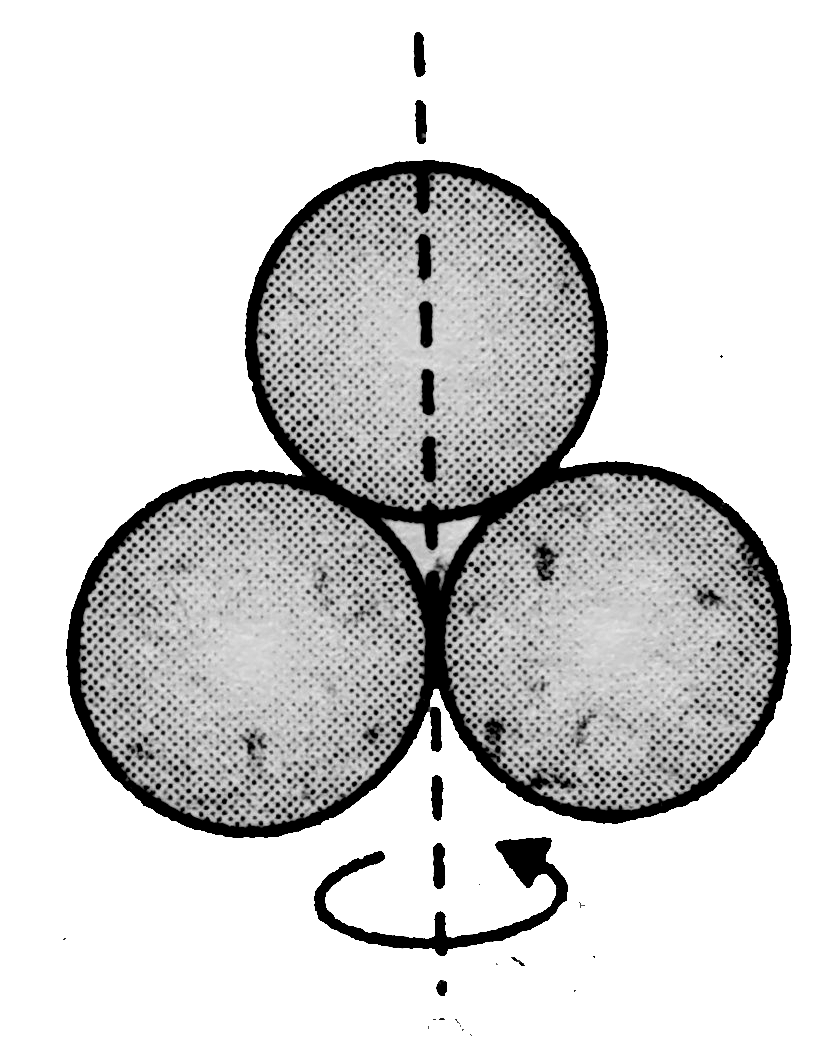
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
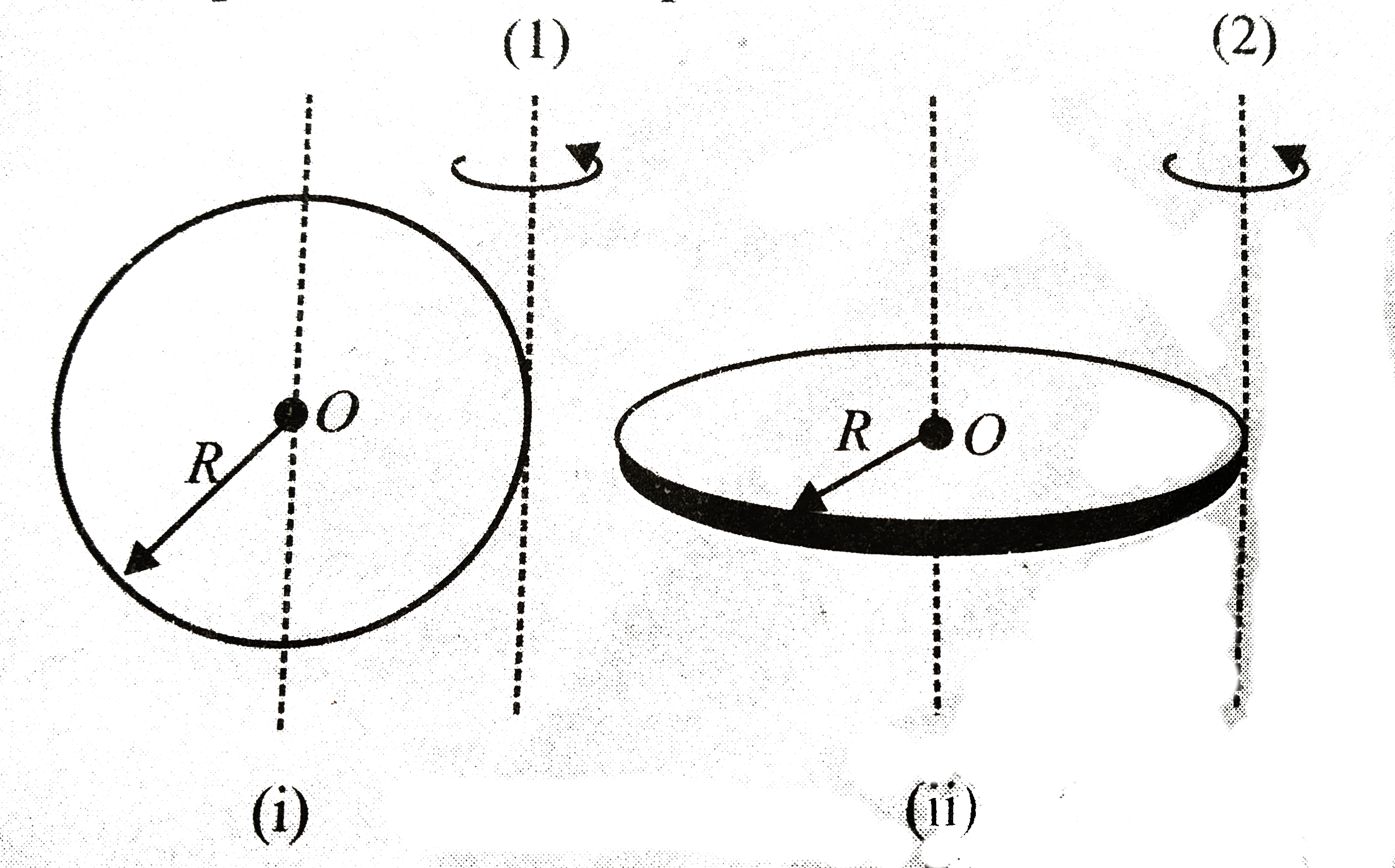
View Solution
